Глава 7. Технология программирования итерационных циклов

Итерационный – циклический процесс, число повторений в котором зависит от результатов счёта в теле цикла и до окончания вычислений не может быть определено.

Принципиальное отличие итерационных циклов от арифметических – величина, используемая в качестве параметра. В арифметических циклах параметрами являются аргументы искомых функций (х_i), а в итерационных – сами функции (y_i).

Это отличие формулирует возможные варианты итерационных циклов:

искомая функция достижима (решение точное);

искомая функция недостижима (приближенное решение).

Схема возможных вариантов представлена на рис. 7.1:

Рис. 7.1. Классификация по точности решения

Итерационный цикл с точным решением – вычислительный процесс, позволяющий достигнуть (превысить) искомое значение функции.

Итерационный цикл с приближенным решением – вычислительный процесс, в котором достигнуть искомое значение функции невозможно, можно лишь приблизиться к нему.

Пути вычисления значений функции итерационного цикла:

· с использованием аргумента;

· рекуррентно.

Графическая интерпретация представлена на рис. 7.2:

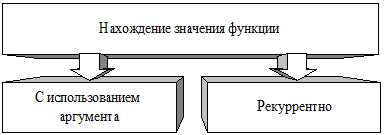
Рис. 7.2. Организация вычисления функции

Вычисления с использованием аргумента – расчет текущих значений функции по математической зависимости аналогичной используемой в арифметических циклах

y_i = f(x_i).

Принципиальное отличие – диапазон изменения аргумента (x_i) до начала счета задан только одним значением – начальным x_i = x_н (i = 1). Стандартный закон изменения x_i = f(x_i-1) (i = i + 1) сохраняется, но не имеет заданного конечного значения x_k (N). Прекращение наращивания аргумента (x_i) определяется не им самим, а рассчитываемым значением функции (y_i) в момент достижения граничного значения (y_гр). Следовательно, условие выхода из цикла есть зависимость:

.

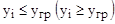Рекуррентные вычисления – расчёт текущих значений функции методом последовательного приближения. Математическое представление:

y_i = f(y_i-1),

предписывает нахождение последующих значений функции через предыдущие значения.

В принципе процесс возможен в двух вариантах

диапазон изменения i конечен;

диапазон изменения i бесконечен.

В первом варианте решение стремится к достижимому (заранее известному) конечному значению функции (y_гр), определяя диапазон изменения параметра цикла i зависимостью 1 £ i £ N. В этом варианте рекуррентный вычислительный процесс есть процесс точных вычислений.

Во втором – решение стремится к недостижимому точному значению функции ( 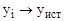) и процесс требует изменения i в диапазоне от единицы до бесконечности 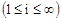. Математически сформулированное условие изменения параметра цикла i технически выполнить невозможно. Завершать решение приходится при некотором значении i, обеспечивающем приближёние текущего значения функции к истинному (недостижимому) в соответствии с заданной степенью точности (e).

.

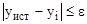В этом варианте рекуррентный вычислительный процесс есть процесс приближённых вычислений.

Ввиду того, что на самом деле точное значение искомой функции y_ист неизвестно, возникает необходимость замены его на реально возможное.

В качестве реально возможного (истинного) предлагается использовать последнее текущее значение y_i. Тогда, сравнивая его с предыдущим, можно получить реальную оценочную зависимость прекращения (продолжения) вычислений

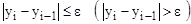
Дополнительно к рассмотренной классификации итерационные циклы по критерию характер результатов можно разделить на сходящиеся и расходящиеся (рис. 7.3).

Рис. 7.3. Классификация по характеру изменения результатов

Сходящийся – итерационный циклический процесс, в котором значения формирующих функцию текущих элементов уменьшаются по модулю.

Расходящийся – итерационный циклический процесс, в котором значения формирующих функцию текущих элементов увеличиваются по модулю.

Графическая интерпретация представлена на рис. 7.4, 7.5.

Внимание! Расходящиеся вычислительные процессы допустимы только в итерационных циклах с точным решением.

Сходящиеся вычислительные процессы – обязательное условие итерационных циклов с приближенным решением.

Число повторений итерационного цикла определяется зависимостью

N = f(y_i),

где N – количество повторений;

y_i – результат вычислений в теле цикла (искомая функция).

Рассмотренные методики позволяют выполнить предмашинную подготовку различных видов задач, реализуемых в виде итерационных циклов. Например, вычисление чисел Фибоначчи, корней нелинейных алгебраических уравнений методом последовательных приближений, расчёт тригонометрических и других трансцендентных функций с помощью численных методов и т. п.

Рассмотрим программирование итерационных процессов на конкретных примерах.