Классификация видов моделирования. Динамические модели. Примеры построения динамических моделей

Классификация видов моделирования может быть проведена по разным основаниям. Модели можно различать по ряду признаков: характеру моделируемых объектов, сферам приложения, глубине моделирования. Рассмотрим 2 варианта классификации. Первый вариант классификации. По глубине моделирования методы моделирования делятся на две группы: материальное (предметное) и идеальное моделирование. Материальное моделирование основано на материальной аналогии объекта и модели. Оно осуществляется с помощью воспроизведения основных геометрических, физических или функциональных характеристик изучаемого объекта. Частным случаем материального моделирования является физическое моделирование. Частным случаем физического моделирования является аналоговое моделирование. Оно основано на аналогии явлений, имеющих различную физическую природу, но описываемых одинаковыми математическими соотношениями. Образец аналогового моделирования – изучение механических колебаний (например, упругой балки) с помощью электрической системы, описываемой теми же дифференциальными уравнениями. Так как эксперименты с электрической системой обычно проще и дешевле, она исследуется в качестве аналога механической системы (например, при изучении колебаний мостов).

Идеальное моделирование основано на идеальной (мысленной) аналогии. В экономических исследованиях (на высоком уровне их проведения, а не на субъективных желаниях отдельных руководителей) это основной вид моделирования. Идеальное моделирование, в свою очередь, разбивается на два подкласса: знаковое (формализованное) и интуитивное моделирование. При знаковом моделировании моделями служат схемы, графики, чертежи, формулы. Важнейшим видом знакового моделирования является математическое моделирование, осуществляемое средствами логико-математических построений.

Интуитивное моделирование встречается в тех областях науки и практики, где познавательный процесс находится на начальной стадии или имеют место очень сложные системные взаимосвязи. Такие исследования называют мысленными экспериментами. В экономике в основном применяется знаковое или интуитивное моделирование; оно описывает мировоззрение ученых или практический опыт работников в сфере управления ею. Второй вариант классификации приведен на рис. 1.3.В соответствии с классификационным признаком полноты моделирование делится на полное, неполное и приближенное. При полном моделировании модели идентичны объекту во времени и пространстве. Для неполного моделирования эта идентичность не сохраняется. В основе приближенного моделирования лежит подобие, при котором некоторые стороны реального объекта не моделируются совсем. Теория подобия утверждает, что абсолютное подобие возможно лишь при замене одного объекта другим точно таким же. Поэтому при моделировании абсолютное подобие не имеет места. Исследователи стремятся к тому, чтобы модель хорошо отображала только исследуемый аспект системы. Например, для оценки помехоустойчивости дискретных каналов передачи информации функциональная и информационная модели системы могут не разрабатываться. Для достижения цели моделирования вполне достаточна событийная модель, описываемая матрицей условных вероятностей ||рij|| переходов i-го символа алфавита j-й.В зависимости от типа носителя и сигнатуры модели различаются следующие виды моделирования: детерминированное и стохастическое, статическое и динамическое, дискретное, непрерывное и дискретно-непрерывное. Детерминированное моделирование отображает процессы, в которых предполагается отсутствие случайных воздействий. Стохастическое моделирование учитывает вероятностные процессы и события. Статическое моделирование служит для описания состояния объекта в фиксированный момент времени, а динамическое - для исследования объекта во времени. При этом оперируют аналоговыми (непрерывными), дискретными и смешанными моделями. В зависимости от формы реализации носителя моделирование классифицируется на мысленное и реальное. Мысленное моделирование применяется тогда, когда модели не реализуемы в заданном интервале времени либо отсутствуют условия для их физического создания (например, ситуация микромира). Мысленное моделирование реальных систем реализуется в виде наглядного, символического и математического. Для представления функциональных, информационных и событийных моделей этого вида моделирования разработано значительное количество средств и методов. При наглядном моделировании на базе представлений человека о реальных объектах создаются наглядные модели, отображающие явления и процессы, протекающие в объекте. Примером таких моделей являются учебные плакаты, рисунки, схемы, диаграммы. В основу гипотетического моделирования закладывается гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Этот вид моделирования используется, когда знаний об объекте недостаточно для построения формальных моделей.

Динамическое моделирование – многошаговый процесс, каждый шаг соответствует поведению экономической системы у определенный временный период. Каждый текущий шаг получает результаты предыдущего шага, который по определенным правилам определяет текущий результат и формирует данные для следующего шага.

Таким образом, динамическая модель в ускоренном режиме позволяет исследовать развития сложной экономической системы, скажем, предприятия, на протяжении определенного периода планирования в условиях изменения ресурсного обеспечения (сырья, кадров, финансов, техники), и получение результаты представить у соответствующему плане развития предприятия на заданный период.

Для решения динамических задач оптимизации в математическом программировании сформировался соответствующий класс моделей под названием динамическое программирование, его основателем стал известный американский математик Р. Беллман. Им предложен специальный метод решения задача этого класса на основе «принципа оптимальности», согласно которого оптимальное решение задачи находится путем ее разбиения на n этапов, каждый с которых представляет подзадачу относительно одной переменной. Расчет выполняется таким образом, что оптимальный результат одной подзадачи является исходными данными для следующей подзадачи с учетом уравнений и ограничений связи между ними, результат последней из них является результатом всей задачи. Общим для всех моделей этой категории является то, что текущие управляющие решения "проявляются" как в период, относящийся непосредственно к моменту принятия решения, так и в последующие периоды. Следовательно, наиболее важные экономические последствия проявляются в разные периоды, а не только в течение одного периода. Такого рода экономические последствия, как правило, оказываются существенными в тех случаях, когда речь идет об управляющих решениях, связанных с возможностью новых капиталовложений, увеличения производственных мощностей или обучения персонала с целью . создания предпосылок для увеличения прибыльности или сокращения издержек в последующие периоды.

Типичными областями применения моделей динамического программирования при принятии решений являются:

Разработка правил управления запасами, устанавливающих момент пополнения запасов и размер пополняющего заказа.

Разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию.

Определение необходимого объема запасных частей, гарантирующего эффективное использование дорогостоящего оборудования.

Распределение дефицитных капитальных вложений между возможными новыми направлениями их использования.

Выбор методов проведения рекламной кампании, знакомящей покупателя с продукцией фирмы.

В задачах, решаемых методом динамического программирования, значение целевой функции (оптимизируемого критерия) для всего процесса получают простым суммированием частных значений fi(x) того же критерия на отдельных шагах, то есть

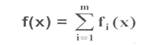
Если критерий (или функция) f(x) обладает этим свойством, то его называют аддитивным (аддитивной).

Алгоритм динамического программирования

1. На выбранном шаге задаем набор (определяемый условиями-ограничениями) значений переменной, характеризующей последний шаг, возможные состояния системы на предпоследнем шаге. Для каждого возможного состояния и каждого значения выбранной переменной вычисляем значения целевой функции. Из них для каждого исхода предпоследнего шага выбираем оптимальные значения целевой функции и соответствующие им значения рассматриваемой переменной. Для каждого исхода предпоследнего шага запоминаем оптимальное значение переменной (или несколько значений, если таких значений больше одного) и соответствующее значение целевой функции. Получаем и фиксируем соответствующую таблицу.

2. Переходим к оптимизации на этапе, предшествующем предыдущему (движение "вспять"), отыскивая оптимальное значение новой переменной при фиксированных найденных ранее оптимальных значениях следующих переменных. Оптимальное значение целевой функции на последующих шагах (при оптимальных значениях последующих переменных) считываем из предыдущей таблицы. Если новая переменная характеризует первый шаг, то переходим к п.З. В противном случае повторяем п.2 для следующей переменной.

З. При данном в задаче исходном условии для каждого возможного значения первой переменной вычисляем значение целевой функции. Выбираем оптимальное значение целевой функции, соответствующее оптимальному(ым) значению(иям) первой переменной.

4. При известном оптимальном значении первой переменной определяем исходные данные для следующего (второго) шага и по последней таблице - оптимальное(ые) значение(ия) следующей (второй) переменной.

5. Если следующая переменная не характеризует последний шаг, то переходим к п.4.Иначе переходим к п.6.

6.Формируем (выписываем) оптимальное решение.

Список использованной литературы

1. Microsoft Office 2010. Самоучитель. Ю. Стоцкий, А. Васильев, И. Телина. Питер. 2011, - 432 с.

2. Фигурнов В.Э. IBM PC для пользователя. Изд-е 7-е. - М.: Инфра-М, 1995.

3. Левин А. Самоучитель работы на компьютере. М. : Нолидж, 1998, - 624 с.

4. Информатика: практикум по технологии работы на персональном компьютере /Под ред. проф. Н.В.Макаровой - М. : Финансы и статистика, 1997 г. - 384с.

5. Информатика: Учебник / Под ред. проф. Н.В. Макаровой - М. : Финансы истатистика, 1997 г. - 768 с.