Дифракционный интеграл Френеля

Принцип Гюйгенса-Френеля позволяет построить элементарную теорию дифракции света. Основная задача теории дифракции ставится так. Пусть имеется точечный источник света S. Требуется найти световое поле в некоторой точке Р, если между точками S и Р расположено препятствие распространению света, например экран с отверстием или непрозрачный диск. Сначала рассмотрим математическую формулировку принципа Гюйгенса-Френеля.

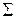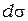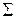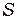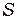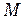Введем некоторую произвольную замкнутую поверхность , охватывающую источник света, и будем считать каждый элемент этой поверхности источником вторичной сферической световой волны (Рис. 2.1) рассмотрим некоторую точку М на поверхности . Считая источник света точечным, обозначим расстояние от до через 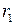, а расстояние от 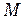до точки наблюдения 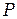через 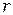. Введем также угол 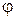между нормалью 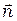к поверхности 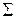в точке 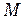и направлением на точку наблюдения 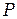. Для простоты будем считать, что источник света испускает монохроматическую волну.

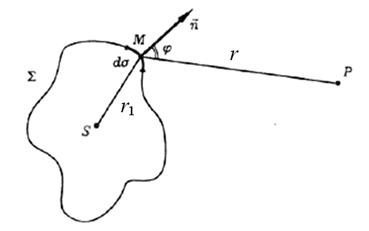
Рис. 2.1. К выводу интеграла Гюйгенса – Френеля

Принцип Гюйгенса-Френеля утверждает, что световое поле в точке 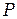- есть результат наложения (сложения) световых волн, испускаемых всеми элементами поверхности 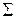. Волну, испускаемую элементом поверхности 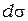, можно считать сферической. Поэтому можно записать, что суммарная амплитуда электрического поля в точке :

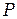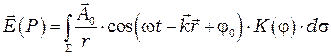
где 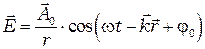- уравнение сферической волны, испускаемой элементом поверхности 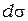, 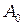- константа равная амплитуде при 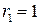(размерность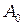 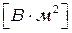), Используя формулу Эйлера, 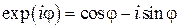запишем эту же формулу в комплексном виде:

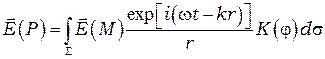(2.1)

Здесь 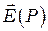и 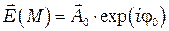— комплексные амплитуды поля в точках Р и М; 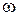и 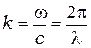- частота и волновое число световой волны, 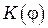- "коэффициент наклона", монотонно убывающий от некоторого начального значения 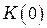до нуля при изменении угла 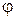от нуля до 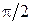. Этот коэффициент учитывает то обстоятельство, что вклад элемента 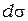в результирующее поле зависит от ориентации данного элемента поверхности по отношению к направлению на точку наблюдения. Из теории Кирхгофа, приближённого решения волнового уравнения Максвелла, следует, что 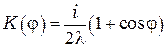. Для параксиальных пучков света, когда 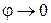угловой коэффициент .

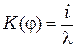Интеграл (2.1) называют интегралом Гюйгенса-Френеля. Формула (2.1) получена на основе качественных физических соображений. Множитель 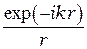в подынтегральном выражении описывает распространение элементарной вторичной сферической световой волны в пространстве. Наиболее существенно то, что интеграл Гюйгенса-Френеля учитывает фазы элементарных вторичных волн, приходящих в точку 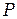от различных элементов поверхности 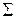, т.е. принимается во внимание интерференция вторичных волн.

Суть принципа Гюйгенса—Френеля записанная в (2.1) в следующем: для определения амплитуды колебания в точке 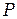, лежащей перед некоторой поверхностью 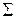, надо найти амплитуды колебаний, приходящих в эту точку от всех элементов 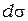поверхности 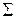и затем сложить их с учетом амплитуд и фаз. При этом предполагается, что все волны испускаемые элементами поверхности 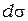взаимно когерентны. Это необходимое условие для интерференции вторичных волн.

Принцип Гюйгенса-Френеля можно представить в простой и наглядной форме с помощью векторной (фазовой) диаграммы (рис. 2.2). Использование подобных диаграмм в дальнейшем позволит значительно упростить многие рассуждения и расчеты. На этой диаграмме результирующая амплитуда - вектор 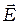, представлен как векторная сумма амплитуд 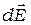элементарных колебаний в точке 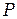от различных элементов 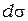поверхности 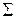с учетом их фаз, т. е. углов между ними.

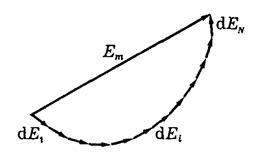
Рис. 2.2

Интеграл (2.1) выражает собой математическую формулировку принципа Гюйгенса-Френеля. Взяв этот интеграл можно рассчитать распределение амплитуды световой волны в плоскости наблюдения. Однако практически рассчитать это интеграл оказалось возможным только для самых простых случаев. Френель предложил хотя и приближенный, но изящный способ расчета дифракционных картин, основанный на представлении о так называемых полуволновых зонах или зонах Френеля.

Метод зон Френеля

Суммирование (интегрирование) амплитуд элементарных колебаний, приходящих в точку 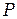,вообще говоря, весьма сложно. Но в простейших случаях, обладающих определенной симметрией, интегрирование, как показал Френель, может быть заменено простым алгебраическим или графическим сложением (последнее особенно наглядно). Суммирование амплитуд колебаний, приходящих от различных элементов волновой поверхности 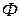, Френель предложил делать с помощью разбиения волновой поверхности 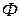на зоны, конфигурация которых зависит от симметрии рассматриваемой задачи. Пользуясь методом Френеля, определим амплитуду световых колебаний в точке 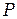за круглым отверстием на его оси (рис. 3.1).

Если рассматривать точечный источник света S, то в качестве поверхности 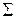удобно взять сферу 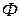, совпадающую со сферическим фронтом волны, излученной источником 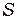. На рис. 3.1 показана часть этого волнового фронта. Рассмотрим в произвольной точке 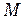амплитуду световой волны, распространяющейся в однородной среде из точечного источника S. Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности 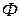, являющейся поверхностью фронта волны, идущей из S. Очевидно, что на сферической поверхности 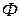амплитуды и фазы колебаний вторичных источников будут одинаковы, поэтому, остаётся учесть только изменение фазы из-за разности хода от различных точек волнового фронта до точки М.

Разобьём волновую поверхность 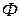на кольцевые зоны, такого размера, чтобы расстояния от краев зоны до точки 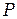отличались на 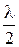. Так как связь между разностью фаз 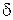разностью хода 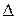определяется выражение

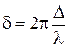, (3.1)

то при разности хода 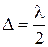разность фаз равна 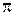. Поэтому вторичные волны, излучаемые с краёв зон, приходят в точку 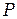в противофазе и гасят друг друга.

Можно показать, что площади всех зон Френеля одинаковы и приближённо равны:

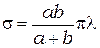(3.2)

где 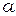- длина отрезка 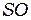- радиус сферы 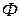, 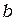- длина отрезка 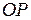– расстояние от поверхности волнового фронта до точки наблюдения, поэтому вклад в суммарную амплитуду каждой зоны будут примерно одинаковы.

φ

О

Ф

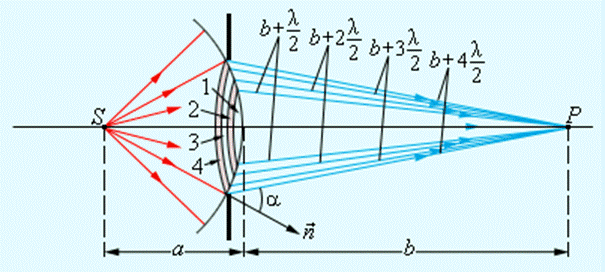
Рис. 3.1. Схема построения зон Френеля

Угол 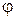между нормалью к поверхности волнового фронта и направлением на точку Р растёт с ростом 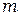, поэтому амплитуда колебаний возбуждаемых 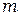-ной зоной убывает с ростом 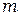, и при 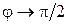число зон 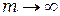и тогда 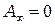. Это значит, что амплитуды колебаний, возбуждаемые зонами Френеля, образуют слабо убывающую последовательность

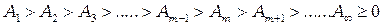(3.3)

Поскольку разность хода от краёв зон равна 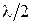то, фазы колебаний, возбуждаемых соседними зонами, отличаются на 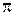, т.е. находятся в противофазе. Это значит что колебания, возбуждаемые первой зоной, будут подавляться колебания возбуждаемыми второй зоной, колебания второй зоны колебаниями третьей зоной и т.д. Амплитуда результирующего колебания, при 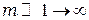, может быть представлена в виде:

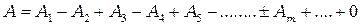(3.4)

Последний член равен нулю, потому что угол между нормалью к излучающей волновой поверхности и направлением на точку наблюдения становится равным и угловой коэффициент 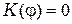, т. е. этот элемент поверхности не излучаете волн в направлении на точку наблюдения.

Заметим, что в выражении (3.4) все амплитуды от нечётных зон входят со знаком плюс, а от чётных зон со знаком минус. Пусть открытыми у нас будет 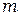зон. Перепишем выражение (3.4) в другом виде:

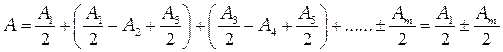(3.5)

где 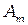амплитуда последней открытой зоны. Поскольку амплитуда возбуждаемых колебаний монотонно убывает 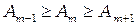можно приближённо считать что:

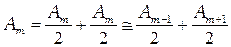. (3.6)

Тогда выражения в скобках равны нулю и если 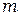нечётное число, то в центре будет светлое пятно за счёт дополнительно вклада 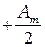, а если 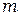чётное – то в центре тёмное пятно из–за вычитания амплитуды создаваемой последней открытой зоны .

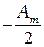При 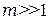, угловой коэффициент 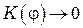, поэтому 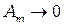и из формулы (3.5) следует:

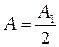. (3.7)

Из формулы (3.7) следует глобальный вывод: когда волновой фронт полностью открыт ( 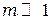) результирующая амплитуда, от всего волнового фронта, равна половине амплитуде создаваемой первой зоной.Это значит, что при свободном распространении волны волновое возмущение от всего волнового фронта составляет половину возмущения, даваемого только первой зоной Френеля. Дело происходит так, как если бы из всего волнового фронта действующей осталось только часть первой зоны Френеля.

Рассмотренные выше рассуждения, выполненные Френелем, можно расценивать как алгебраический способ определения амплитуды световой волны. Кроме этого существует более наглядный графический способ, основанный на методе вращающего вектора амплитуды или методе векторных диаграмм.