Задачи повышенной сложности. 1) Написать программу нахождения суммы большего и меньшего из 3 чисел.
1) Написать программу нахождения суммы большего и меньшего из 3 чисел.
2) Найти max{min(a, b), min(c, d)}.
3) Даны три числа a, b, c. Определить, какое из них равно d. Если ни одно из них не равно d, то найти max(d-a, d-b, d-c).
4) Даны числа x, y, z. Найти значение выражения:
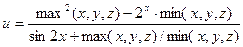
5) Написать программу, которая по заданным трем числам определяет, является ли сумма каких-либо двух из них положительной.
6) На оси OX расположены три точки a, b, c. Определить, какая из точек b, c расположена ближе к a.
7) Даны действительные числа a, b, c. Удвоить эти числа, если a<b<c, и заменить их абсолютными значениями, если это не так.
Лабораторная работа № 3
Тема: Операторы повторений
Задание.
Составить схему алгоритма и программу а языке Паскаль для вычисления значений функции y=f(x) в точках от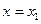 
до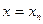 
c шагом 
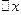. При выполнении задания использовать операторы цикла с постусловием, с предусловием и оператор цикла с параметром.
Результаты вычислений оформить в виде таблицы, используя символы псевдографики. Коды символов приведены в таблице. Для вставки нужного символа в текст программы держите нажатой клавишу ALT при наборе кода. Код набирать на ЦИФРОВОЙ КЛАВИАТУРЕ. Коды символов приведены в таблице 3.1.
Таблица 3.1
| Одинарная рамка | Двойная рамка | Горизонтальные элементы | Вертикальные элементы |
| ┌ ┬ ┐ 218 194 191 ├ ┼ ┤ 195 197 180 └ ┴ ┘ 192 193 217 | ╔ ╦ ╗ 201 203 187 ╠ ╬ ╣ 204 206 185 ╚ ╩ ╝ 200 202 188 | ─ 196 ═ 205 | │ 179 ║ 186 |
Варианты заданий к лабораторной работе № 3
Таблица 3.2
| Номер варианта | y = f(x) | Исходные данные |
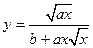 | x1 = 1; xn = 2; Δx = 0,2; a = 3,5; b = 1,2 | |
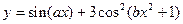 | x1 = 0; xn = 5; Δx = 0,5; a = 0,5; b = 0,7 | |
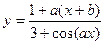 | x1 = 1; xn = 3; Δx = 0,2; a = 3,9; b = 2,3 | |
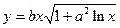 | x1 = 2; xn = 3; Δx = 0,1; a = 4; b = 7 | |
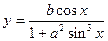 | x1 = 1; xn = 6; Δx = 0,5; a = 0,57; b = 9 | |
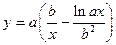 | x1 = 2; xn = 5; Δx = 0,5; a = 1,5; b = 4,8 | |
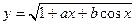 | x1 = 2; xn = 8; Δx = 0,7; a = 4,2; b = 1,5 | |
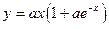 | x1 =2; xn = 7; Δx = 0,5; a = 3,5; | |
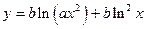 | x1 = 1; xn = 4; Δx = 0,3; a =4,3; b = 5,4 | |
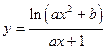 | x1 = 2; xn = 4; Δx = 0,4; a = 1,4; b = 2,5 | |
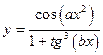 | x1 = 0; xn = 1; Δx = 0,1; a = 2,1; b = 0,3 | |
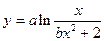 | x1 = 3; xn = 6; Δx = 0,3; a = 1,9; b = 1,1 | |
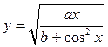 | x1 = 3; xn = 5; Δx = 0,2; a = 1,9; b = 1,1 | |
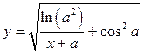 | x1 = 5; xn = 8; Δx = 0,2; a = 5,3; | |
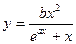 | x1 = 2; xn = 8; Δx = 0,6; a = 1,9; b = 1,1 | |
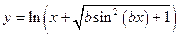 | x1 = 1; xn = 5; Δx = 0,4; b = 5,7 | |
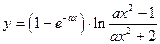 | x1 = 4; xn = 7; Δx = 0,3; a = 3,8 | |
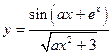 | x1 = 3; xn = 9; Δx = 0,6; a = 2,7 | |
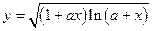 | x1 = 1; xn = 5; Δx = 0,4; a = 5,3 | |
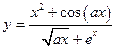 | x1 = 2; xn = 4; Δx = 0,1; a = 4,5 | |
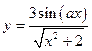 | x1 = 3; xn = 5; Δx = 0,1; a = 4,5 | |
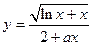 | x1 = 1; xn = 3; Δx =0,2; a = 2,8 | |
 | x1 = 3; xn = 9; Δx = 0,3; b = 0,71 | |
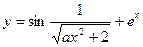 | x1 = 0; xn = 3; Δx = 0,2; a = 3,9 | |
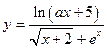 | x1 = 5; xn = 9; Δx = 0,4; a = 2,4 | |
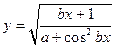 | x1 = 1; xn = 3; Δx = 0,2; a = 4,1; b = 4,7 | |
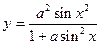 | x1 = 0; xn = 2; Δx = 0,2; a = 1,92 | |
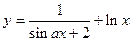 | x1 = 1; xn = 4; Δx = 0,3; a = 1,8 | |
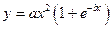 | x1 = 1; xn = 3; Δx = 0,2; a = 0,8; b = 4,2 | |
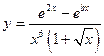 | x1 = 1; xn = 5; Δx = 0,4; b = 0,37 |
Пример решения задачи
Задание: Составить схему алгоритма для вычисления значений функции
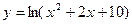от значения x1 = 1 до значения xn = 5 с шагом Δx=0,5.
Решение: Блок-схемы алгоритмов вычислений и тексты программ с использованием операторов цикла while, repeat, for приведены ниже.
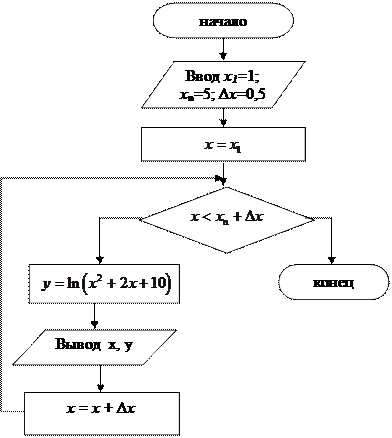
1) While
Рисунок 3.1
Да Нет
|
Текст программы:
program p3a;
var x,y,x1,xn,dx:real;
begin
write(‘Введите начальное, конечное и шаг=’);
readln(x1,xn,dx);
x:=x1;
writeln(' Таблица');
writeln('┌─────┬─────┐');
writeln('│ X │ Y │');
while x<(xn+dx) do
begin
y:=ln(sqr(x)+2*x+10);
writeln('├─────┼─────┤');
writeln('│',x:5:2,'│',y:5:2,'│');
x:=x+dx;
end;
writeln('└─────┴─────┘');
readln;
end.
2) Repeat
Рисунок 3.2
 |
|
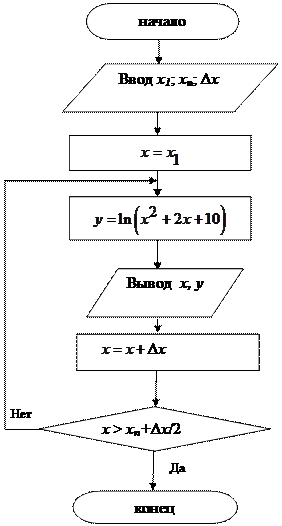Текст программы:
program p3a;
var x,y,x1,xn,dx:real;
begin
write(‘Введите начальное, конечное и шаг=’);
readln(x1,xn,dx);
x:=x1;
writeln(' Таблица');
writeln('┌─────┬─────┐');
writeln('│ X │ Y │');
repeat
y:=ln(sqr(x)+2*x+10);
writeln('├─────┼─────┤');
writeln('│',x:5:2,'│',y:5:2,'│');
x:=x+dx;
until x>xn+dx/2;
writeln('└─────┴─────┘');
readln;
end.
Результат выполнения контрольного примера:
Таблица
┌─────┬─────┐
│ X │ Y │
├─────┼─────┤
│ 1.00 │ 2.56 │
├─────┼─────┤
│ 1.50 │ 2.72 │
├─────┼─────┤
│ 2.00 │ 2.89 │
├─────┼─────┤
│ 2.50 │ 3.06 │
├─────┼─────┤
│ 3.00 │ 3.22 │
├─────┼─────┤
│ 3.50 │ 3.38 │
├─────┼─────┤
│ 4.00 │ 3.53 │
├─────┼─────┤
│ 4.50 │ 3.67 │
├─────┼─────┤
│ 5.00 │ 3.81 │
└─────┴─────┘
3)For
Рисунок 3.3
 |
|
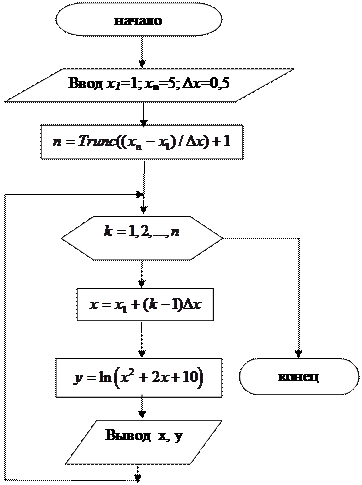Текст программы:
program p3a;
var x,y,x1,xn,dx:real;
k,n:integer;
begin
write(‘Введите начальное, конечное и шаг=’);
readln(x1,xn,dx);
n:=Round((xn-x1)/dx)+1;
writeln(' Таблица');
writeln('┌────┬─────┐');
writeln('│ X │ Y │');
for k:=1 to n do
begin
x:=x1+(k-1)*dx;
y:=ln(sqr(x)+2*x+10);
writeln('├─────┼─────┤');
writeln('│',x:5:2,'│',y:5:2,'│');
end;
writeln('└─────┴─────┘');
readln;
end.