Функция ненадежности элемента

Введем отношение 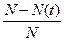, представляющее долю или частоту отказавших к моменту t элементов от общего их числа N. Эта доля равна 0 при t=0 (ибо в работу включают только исправные элементы) и равна 1 при t=t_m, т.е. к моменту окончания эксперимента или отказу всех N испытуемых элементов. Так как эта доля зависит от времени t, то обозначим ее через

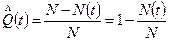
и назовем статистической функцией распределения отказов.

Устремим число испытуемых элементов к бесконечности: 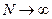. Тогда при 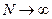статистическое распределение отказов сходится равномерно по вероятности к закону распределения вероятностей отказов элемента

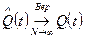=Вер{того, что Т<t}.

Интегральный закон распределения вероятностей отказов элемента до некоторого момента времени t: Q(t)=Вер{Т<t} называют функцией ненадежности элемента или функцией рискаэксплуатации элемента (рис. 2.19).

При t=0 имеем: Т<0 – невозможное случайное событие (ибо в работу включаются только исправные элементы) и поэтому Q(0)=0.

При 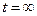имеем: Т<¥ - достоверное событие, заключающееся в отказе всех материальных элементов за бесконечно большое время эксплуатации ("нет ничего вечного в этом мире"!), следовательно: Q(+¥)=1 .

Функция ненадежности в общем случае неубывающая непрерывная функция времени t, 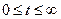( рис. 2.19)

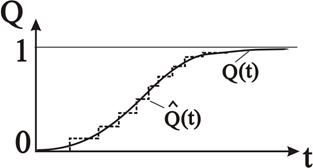
Рис. 2.19 – Функция ненадежности элемента

Статистическая функция ненадежности 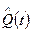является кусочно-постоянной неубывающей функцией времени, показанной пунктиром на рис. 2.19. Отметим еще раз, что Q(t) – неслучайная, а 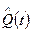- случайная функция. В реальных условиях функция Q(t) нам не известна и мы всегда работаем с ее оценкой .

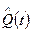Функция ненадежности Q(t) наиболее полно описывает поведение случайной величины Т. Она позволяет, в частности, определять все другие (рассматриваются ниже) функциональные и числовые показатели надежности, а также дает ответ на практически важные вопросы:

какие элементы с разными функциями риска менее надежны;

сколько элементов N₀ из N работающих откажут к данному моменту времени t₀ ( );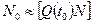

сколько элементов 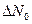откажет на отрезке времени 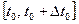(для этого ).

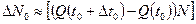Функция надежности элемента

Вернемся снова к экспериментальным данным N, N(t), N-N(t), t_m и введем долю или частоту не отказавших к моменту времени t элементов 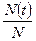. Эта доля

равна 1 при t=0 (в работу включили только исправные элементы!) и нулю при t=+¥ (все материальное разрушается). Зависимость 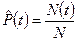, 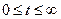назовем статистической функцией надежности, она, как уже показано, изменяется от 1 до 0.

При N®¥ функция 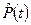сходится по вероятности к интегральному закону распределения вероятностей безотказной работыилифункции надежности P(t)

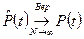=Вер{того, что Т>t}=Вер{Т>t}.

Функция надежности 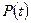=Вер{Т>t} равна 1 при t=0 и 0 при t=¥. (рис 2.20). Эта функция невозрастающая и непрерывная. Статистическая зависимость 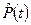является кусочно-постоянной функцией (показана пунктиром на рис. 2.20):

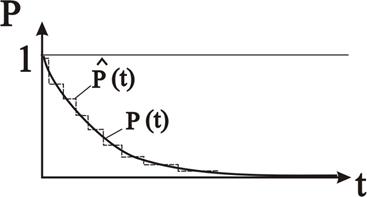
Рис. 2.20 – Функция надежности элемента

Согласно определению каждый элемент может находиться в одном из двух состояний: работоспособности и отказа. Эти случайные независимые несовместные события образуют полную группу событий и тогда .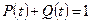

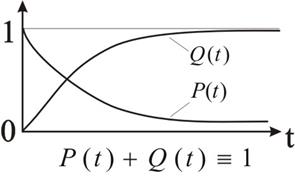
Рис. 2.20 а – К понятию полной группы случайных событий

Плотность вероятности отказа f(t)

При решении многих задач надежности оказывается удобным применять не интегральные распределения P(t), Q(t), а дифференциальный закон распределения вероятности отказа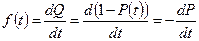

Эту зависимость часто называют плотностью вероятностей отказа. Функция f(t) определена на отрезке времени [0, +¥] и всегда положительна. Кроме того, по определению

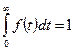
По сравнению с P(t) и Q(t), функция плотности не содержит новой информации. Если известна f(t), то нетрудно найти

,

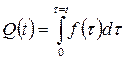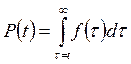
Функция плотности f(t) показана на рис. 2.21 штрихпунктирной линией.

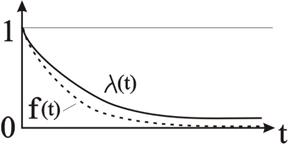
Рис. 2.21 – Функции плотности вероятности отказа 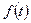и интенсивности отказа 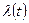(лямбда-характеристика)

Статистическая плотность распределения 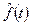находится по экспериментальным данным

,

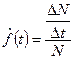где t – середина малого интервала времени 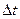, на котором имело место 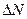отказов элементов. При N®¥ и 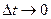функция распределения 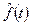сходится в вероятности к f(t). Отметим, что f(t) имеет физическую размерность .

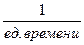Интенсивность отказов

Для описания поведения случайной величины Т часто используют функцию интенсивности отказов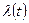

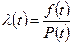
представляющую условную плотность вероятности отказа элемента в момент t при условии, что до этого времени элемент не отказал. (рис. 2.21).

Функцию интенсивности отказов 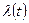обычно называют лямбда-характеристикой.

Статистическая лямбда-характеристика 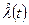определяется по результатам испытания N одинаковых элементов на надежность:

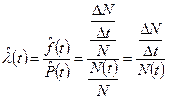
При N®¥ и 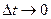статистическая функция .

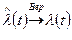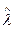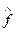Из формул для вычисления оценок и следует, что 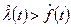для всех t, 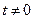; при t=0 функции 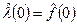, ибо N(0)=N.

Рассмотренная особенность верна и для неслучайных функций l(t) и f(t) (см. рис. 2.21): , , .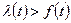

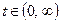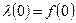Кроме того, 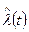всегда положительная функция, имеющая особенности в виде разрывов второго рода: при N(t)®0 функция .

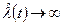Функция интенсивности l(t) имеет физическую размерность 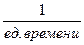. Если время t измеряется числом включений дискретного элемента (реле) или числом циклов элемента с периодическим режимом функционирования, то и l(t) имеет соответствующую размерность: , .

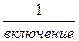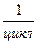Знание функции интенсивности позволяет находить любые другие характеристики надежности. Определим по l(t) функцию надежности P(t):

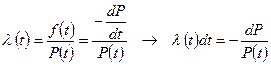
Возьмем интегралы от левой и правой частей последнего равенства

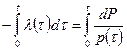
В правой части под знаком интеграла находится так называемая логарифмическая производная, поэтому 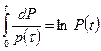. Выражение 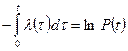после потенцирования принимает вид:

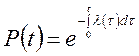
Далее находим 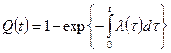и .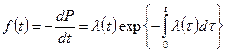

Взаимосвязи между показателями надежности приведены в табл. 1.

Известная функция	Другие функциональные показатели надежности
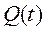	P(t)=1-Q(t)	f(t)=	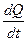λ(t)=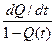
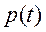	Q(t)=1-P(t)	f(t)= -	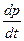λ(t)=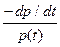
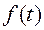	Q(t)=	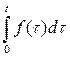P(t)=	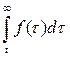λ(t)=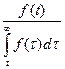
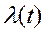	Q(t)=	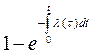P(t)=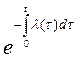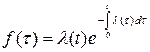

Таблица 1