Сетевые модели. Алгоритмы на графах

(4 часа)

Цель работы: Освоить на практике основные структуры данных для хранения графовых моделей в вычислительной системе, так же базовые алгоритмы для обхода графа и задачи, базирующиеся на них

Домашнее задание:

1.Изучить структуры данных для представления ориентированных и неориентированных графов.

2.Изучить базовые алгоритмы обхода графов: поиск в ширину , поиск в глубину.

3.Разобраться в реализации задач построения каркасов в графе, построения каркаса минимального веса ,нахождения циклов различной природы в графе.

4.Изучить алгоритм Дейкстры- нахождение кратчайших путей во взвешенном графе.

Порядок выполнения работы.

1.Открыть проект Delphi Structures.

2.Добавить в управляющее главное меню пункт «Лабораторная работа №9», при выборе которого должно появляться окно модуля «Graph» (модуль «Graph» с формой добавить в проект).

3.Установить на форму модуля Hesh компоненты, обеспечивающие ввод исходных данных, управляющую кнопку (класса TButton или TBitBtn) и компоненты для вывода результатов на экране в соответствии с вариантом задания таблицы №9.1.

4.В обработчике события onClick управляющей кнопки на языке

Object Pascal написать фрагмент программы для реализации алгоритма обработки графа в соответствии с вариантом задания.

5.Отладить обработчик на тестовых примерах и продемонстрировать работу приложения преподавателю.

6.произвести анализ запрограммированного алгоритма (по количеству сравнений).

7.Составить отчет и защитить работу преподавателю. В отчете обязательно представить блок-схему алгоритма решения задачи.

Таблица 9.1

№ вар.	Текст задачи
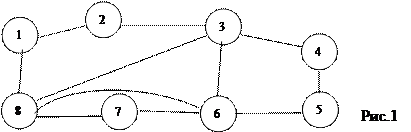
1.	Дан связный неориентированный граф G=(V,E). (рис.1) Граф задан с помощью матрицы смежности. Найти: используя алгоритм поиска в ширину, построить и вывести в объект на форму дерево поиска в ширину
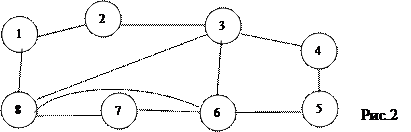
2.	Дан связный неориентированный граф G=(V,E). (рис.2) Граф задан с помощью матрицы смежности. Найти: используя алгоритм поиска в глубину, построить и вывести в объект на форму одиночный каркас( остовное дерево ).
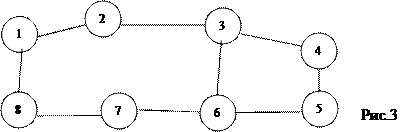
3.	Дан связный неориентированный граф G=(V,E). (рис.3)   Граф задан с помощью списков смежности. Найти: используя алгоритм поиска в глубину, построить и вывести в объект на форму одиночный каркас( остовное дерево ).
4.	Дан связный неориентированный граф G= (V, E).(рис.3)   Найти все каркасы графа.
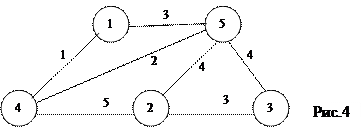
5.	Дан связный неориентированный граф G= (V, E).Ребра имеют вес w (рис.4) Граф описывается перечнем ребер с указанием их веса: P:array[1..3,1..N*(N-1) div 2] of integer; Найти каркас минимального веса, используя алгоритм Крускала.
6.	Дан связный неориентированный граф G= (V, E).Ребра имеют вес w (рис.4) Граф описывается матрицей смежности: P:array[1..N,1..N] of integer; Элемент матрицы не равный нулю ,определяет вес ребра.   Найти каркас минимального веса, используя алгоритм Прима.
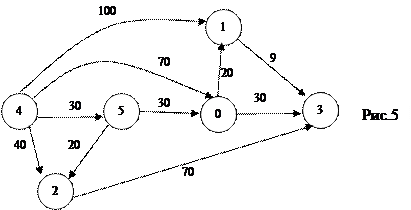
7.	Дан ориентированный граф G=(V,E) с весовой функцией. Граф задан матрицей смежности.(рис.5) Найти массив кратчайших расстояний от вершины с номером 0 до всех остальных вершин алгоритмом Дейкстры.
8.	Пусть G=(V,E) - связный неориентированный граф. Точкой сочленения называется вершина, удаление которой делает граф несвязным.( На рис.6 точки сочленения закрашены.) Используя алгоритм поиска в глубину , найти точки сочленения , если они есть, в графе G.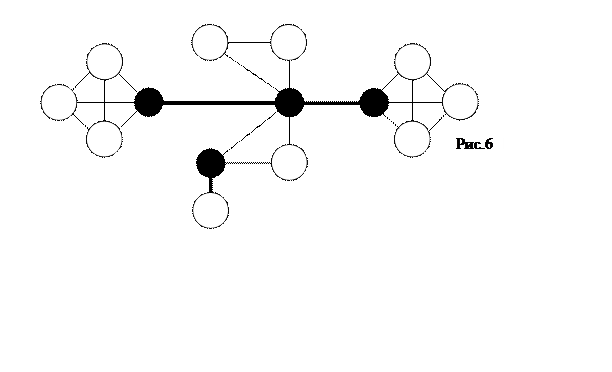
9.	Пусть G=(V,E) - связный неориентированный граф. Мостом графа G называется ребро, удаление которого делает граф несвязным. (На рис.6 мосты выделены.) Используя алгоритм поиска в глубину, найти мосты в графе G.

Контрольные вопросы

1.Каковы особенности представления различных графов с помощью матрицы смежности?

2В чем преимущества и недостатки представления графов с помощью списков смежности?

3.В чем заключается методика раскраски вершин в алгоритме обхода графа поиском в ширину?

4.Что мы называем каркасом или остовом графа?

5.Что такое каркас минимального веса?

6.Что мы называем Эйлеровым циклом и какого условие его существования в графе?

7.Что такое Гамильтонов цикл?

8.Какова цель поиска алгоритмом Дейкстры?