Преобразование чисел из одной системы счисления в другую

Системы счисления

Совокупность приемов записи и наименования чисел называется системой счисления. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Примером непозиционной системы счисления может служить римская: для записи числа один используется буква I, два и три выглядят как II, III, но для записи числа пять выбирается новый символ V, шесть — VI, десять — вводится символ X, сто — С, тысяча — М и т.д. Такой подход не удобен, поскольку бесконечный ряд чисел потребует бесконечного числа символов для записи чисел. Кроме того, такой способ записи чисел приводит к очень сложным правилам арифметики.

Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой, например, 125 и 215. Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем его обозначим q.

В повседневной жизни мы пользуемся десятичной позиционной системой счисления, q = 10, т.е. используется 10 цифр: от 0 до 9.

Рассмотрим правила записи чисел в позиционной десятичной системе счисления. Числа от 0 до 9 записываются цифрами, для записи следующего числа цифры не существует, поэтому вместо 9 пишут 0, но левее нуля образуется еще один разряд, называемый старшим, где записывается (прибавляется) 1, в результате получается 10. Затем пойдут числа 11, 12, но на 19 опять младший разряд заполнится и мы его снова заменим на 0, а старший разряд увеличим на 1, получим 20. Далее по аналогии 30, 40 ... 90, 91, 92 ... до 99. Здесь заполненными оказываются два разряда сразу; чтобы получить следующее число, мы заменяем оба на 0, а в старшем разряде, теперь уже третьем, поставим 1 (т.е. получим число 100) и т.д. Очевидно, что, используя конечное число цифр, можно записать любое сколь но большое число. Выполнение арифметических действий в десятичной системе счисления весьма просто. Число в позиционной системе счисления с основанием q может быть представлено в виде полинома по степеням q. Например, в десятичной системе мы имеем число

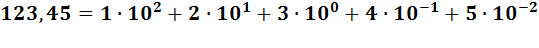
а в общеём виде это правило запишется так:

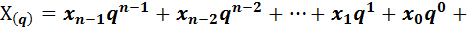
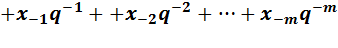(3.1)

Здесь 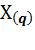— запись числа в системе счисления с основанием ;

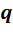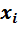— натуральные числа меньше 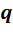, т.е. цифры;

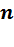— число разрадов целой части;

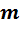— число разрядов дробной части.

Записывая слева направо цифры числа, мы получим закодированную запись числа в 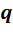-ичной системе счисления:

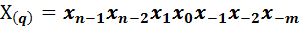
В информатике, вследствие применения электронных средств вычислительной техники, большое значение имеет двоичная система счисления, q = 2. На ранних этапах развития вычислительной техники арифметические операции с действительными числами производились в двоичной системе ввиду простоты их реализации в ЭВМ. Но запись числа в двоичной системе счисления длиннее записи того же числа в десятичной системе счисления в log2 10 раз (примерно в 3,3 раза).

На начальном этапе развития ЭВМ для ввода/вывода информации применялись восьмеричная и шестнадцатеричная системы счисления. Восьмеричная система счисления имеет восемь цифр: 0 1 2 3 4 5 6 7. Шестнадцатеричная — шестнадцать, причем первые 10 цифр совпадают по написанию с цифрами десятичной системы счисления, а для обозначения оставшихся шести цифр применяются большие латинские буквы, т.е. для шестнадцатеричной системы счисления получим набор цифр: 0 1 2 3 4 5 6 7 8 9 A B C D E F.

Одно и то же число 231, записанное в десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления следующим образом:

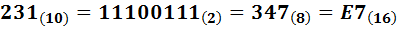
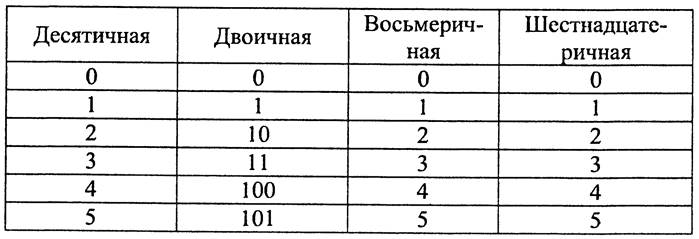
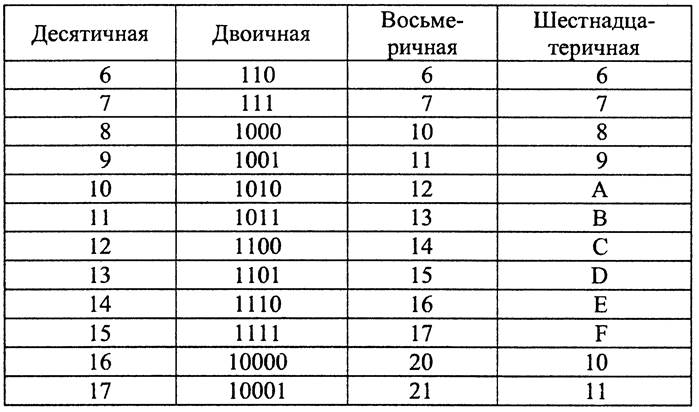
Начало натурального ряда в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления имеет вид:

Диапазон чисел 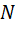, представляемы при помощи n - разрядного кода системы счисления c основанием q находится как:

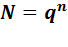
При помощи 3-х разрядов десятичной с/с можно представить 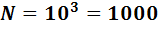чисел от 0 до 999.

При помощи 2-х разрядов двоичной с/с можно представить 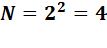чисел: 00, 01, 10, 11.

Преобразование чисел из одной системы счисления в другую

Переход от произвольной ( 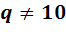) системы счисления к десятичной, удобно выполнять на основе выражения(3.1), например:

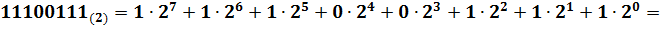
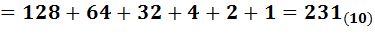
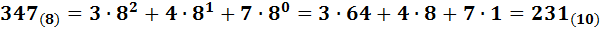
Преобразование из десятичной в прочие системы счисления проводится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.

Рассмотрим алгоритм на примере перевода десятичного числа 231 в двоичную систему (совершенно аналогичен перевод из десятичной системы в любую 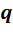-ичную). Разделим число на два (основание системы): нацело 231 : 2 = 115 и остаток 1, т.е. можно записать

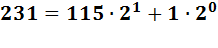
Число 115 (такой двоичной цифры нет) тоже может быть разделено нацело на 2, т.е. 115 : 2 = 57 и остаток 1. И так далее. Запишем процесс деления следующим образом:

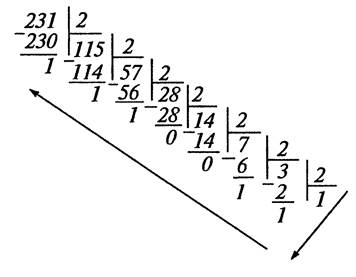
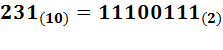
Читая частное и остатки от деления в порядке, обратном получению, получим двоичную запись числа. Такой способ перевода чисел называется правилом (алгоритмом) последовательного деления, очевидно, что он применим для любого основания.

Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения, которое также рассмотрим на примере. Переведем 0,8125 из десятичной системы в двоичную систему счисления. Умножим его на 2, т.е. 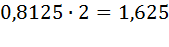или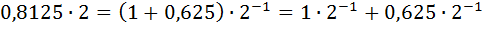

Аналогично 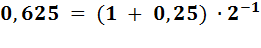или

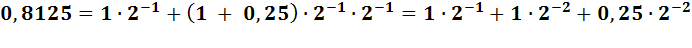или , но 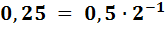и так далее получим правило (алгоритм) последовательного умножения:

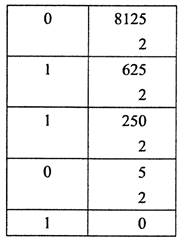
В десятичной системе счисления правильная дробь переводится в десятичную дробь в конечном виде только в том случае, если ее знаменатель в качестве множителей имеет только степени двоек и пятерок, т.е. дробь имеет вид 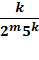. Все же остальные дроби переводятся в бесконечные периодические дроби. Аналогично в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки, т.е. большинство десятичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями.

Если ведутся приближенные вычисления, то последний разряд является сомнительным, и для обеспечения в приближенных вычислениях одинаковой точности в двоичной и десятичной записях числа без бесконечных дробей, достаточно взять число двоичных разрядов в 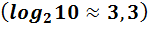4 раза больше, чем десятичных.

Между двоичной системой счисления, с одной стороны, и восьмеричной и шестнадцатеричной (заметим, 8 и 16 — есть третья и четвертая степени двойки) — с другой, существует связь, позволяющая легко переводить числа из одной системы в другую.

Переход от двоичного числа к восьмеричному и шестнадцатеричному производится путем разбиения двоичного числа на триады (три разряда) и тетрады (четыре разряда) соответственно влево и вправо от запятой с последующей заменой триад и тетрад на их символьные эквиваленты в соответствии с табл.3.1. Недостающие позиции в триадах и тетрадах заполняются нулями.

Таблица 3.1. Представление чисел.

10 c/c	2 c/c	8 c/c	16 c/c
			A
			B
			C
			D
			E
			F

Переведем число 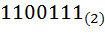в восьмеричную систему счисления. Для этого разобьем двоичное число на триады, начиная слева направо 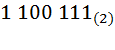. В случае, если в крайней левой триаде не достаточно разрядов, допишем слева недостающие нули 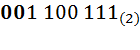. Далее при помощи таблицы 3.1 заменим двоичные триады на их символьные эквиваленты из колонки восьмеричной системы счисления .

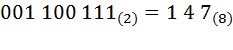Переведем число 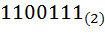в шестнадцатеричную систему счисления. Для этого разобьем двоичное число на титрады, начиная слева направо 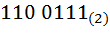. В случае, если в крайней левой титраде не достаточно разрядов, допишем слева недостающие нули 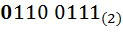. Далее при помощи таблицы 3.1 заменим двоичные титрады на их символьные эквиваленты из колонки шестнадцатеричной системы счисления .

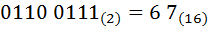Двоичная арифметика

Правила выполнения арифметических действий очень просты. Они задаются таблицами сложения, вычитания и умножения (см.табл.3.2)

Таблица 3.2. Правила представления арифметических операций.

Двоичное сложение	Двоичного вычитания	Двоичного умножения
0 + 0 = 0	0 – 0 = 0	0 * 0 = 0
1 + 0 = 1	1 – 0 = 1	1 * 0 = 0
0 + 1 = 1	1 – 1 = 0	0 * 1 = 0
1 + 1 = 10	10 – 1 = 1	1 * 1 = 1

Правила арифметики во всех позиционных системах аналогичны (10 с/с, 2 с/с, 8 с/с и 16 с/с). Поэтому действия над двоичными числами производятся подобно сложению, вычитанию, умножению и делению целых, дробных десятичных и смешанных чисел в 10 с/с в соответствии с табл.2.2.

Пример. Заданы B = 110,1₂ и C = 10₂.

Вычислить Д1 = B + C, Д2 = B – C, Д3 = B x C, Д4 = B / C.

+			0,			+	6,					-			0,			-	6,
			0,		2		8,		10						0,		2		4,		10
	*			0,			*	6,				110,1 / 10 = 11,012; 6,5 / 2 = 3,2510
+								3,		10		-										-	6,
																1,			2			3,			10
				1,		2							-									-
															-								-

Д1 = 1000,1₂; Д2 = 100,1₂; Д3 = 1101₂; Д4 = 11,01₂.

Благодаря простой двоичной арифметике при работе в 2 с/с упрощаются схемы арифметических устройств.