Скрытие данных с использованием эхо-сигнала

Данный метод подразумевает под собой встраивание данных в аудиосигнал-контейнер путем введения в него эхо-сигнала [14]. Данные скрываются изменением трех параметров эхо-сигнала: начальной амплитуды, скорости затухания [(начальная амплитуда - затухание)/ 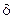] и сдвига (рис. 5.78).

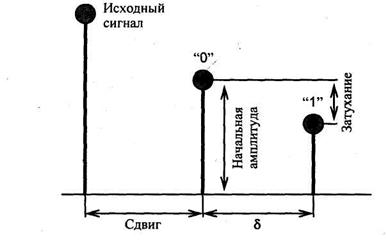
Рис. 5.78 Регулируемые параметры эхо-сигнала

Когда сдвиг (задержка) между первичным и эхо-сигналом уменьшается, начиная с некоторого значения задержки, ССЧ становится не способной обнаружить разницу между двумя сигналами, а эхо-сигнал воспринимается только как дополнительный резонанс. Упомянутое значение трудно определить точно, поскольку оно зависит от качества первичной звукозаписи, типа звука, для которого формируется эхо-сигнал, и, в конечном итоге, — от слушателя.

В общем случае, авторы [14] пришли к выводу, что для большинства звуков и большинства слушателей смешивание происходит при задержке, соответствующей приблизительно одной миллисекунде.

Стеганокодер использует два времени задержки: одно для представления двоичного нуля ("сдвиг" на рис. 5.78), а другое — для представления двоичной единицы ("сдвиг + "). Оба времени задержки меньше того предельного времени, за которое ССЧ способна распознать эхо-сигнал. Кроме уменьшения времени задержки для обеспечения неощущаемости также можно установить уровни начальной амплитуды и времени затухания, которые бы не превышали порог чувствительности ССЧ.

Процесс встраивания данных может быть представлен в виде устройства, которое реализует одну из двух возможных системных функций. Во временной области системные функции — это дискретные во времени экспоненты (рис. 5.79), отличие между которыми состоит лишь в задержке между импульсами.

Рис. 5.79 Дискретный во времени экспоненциал

Рассмотрим пример с двумя импульсами (один для копирования исходного сигнала, а другой — для формирования эхо-сигнала). Очевидно, что увеличение количества импульсов приведет к возрастанию количества эхо-сигналов.

На рис. 5.80 представлены системные функции для кодирования двоичных "1" и "0". Обработка сигнала в соответствии с рис. 5.80, а или б будет иметь своим результатом закодированный сигнал (рис. 5.81).

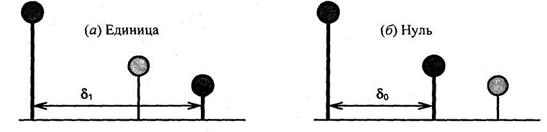
Рис. 5.80 Регулируемые параметры эхо-сигнала

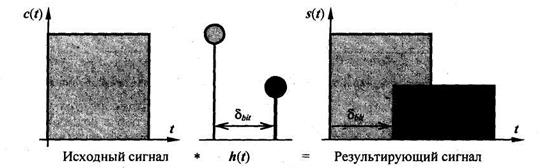
Рис. 5.81 Примеры эхо-отображения

Задержка 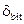между первичным и эхо-сигналом является зависимой от того, какое представление или системная функция была использована. Представление "1" создается задержкой в 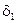секунд, тогда как представление "0" — задержкой в 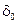секунд.

Для того чтобы в первичный сигнал закодировать более одного бита, сигнал раскладывается на меньшие сегменты. Каждый сегмент при этом рассматривается как отдельный сигнал и в него может быть встроен (путем эхо-отображения) один бит информации. Результирующий закодированный сигнал (содержащий несколько бит) представляет собой новое объединение всех независимо закодированных сегментов исходного сигнала.

На рис. 5.82 изображен пример, при котором сигнал был разделен на 7 равных сегментов, помеченных как а, b, с, d, е, f и g.

Рис. 5.82. Разбиение первичного сигнала на меньшие сегменты для встраивания информации, представляющей собой последовательность двоичных данных

Пусть необходимо, чтобы сегменты а, с, d и g содержали "1". Следовательно, для каждого из них нужно применить системную функцию представления единицы (рис. 5.80, а). Каждый сегмент индивидуально сворачивается с системной функцией. Нули, помещенные в сегменты b, e и f, кодируются аналогично, используя способ представления нуля (рис. 5.80, б).

Полученные после сворачивания с соответствующей функцией результаты повторно объединяются.

Для достижения минимальной заметности повторного объединения, в [14] предварительно предлагается создать отдельные "единичный" и "нулевой" эхо-сигналы, повторяя первичный и используя соответствующие представления "1" и "0". Полученные в результате сигналы изображены на рис. 5.83.

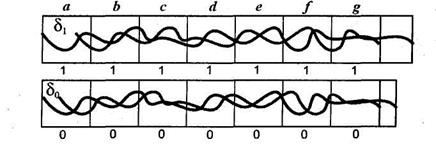
Рис. 5.83. Создание "единичного" и "нулевого" эхо-сигналов (более светлая линия)

"Единичный" и "нулевой" эхо-сигналы содержат, соответственно, только единицы и нули. Для того чтобы объединить эти два сигнала, также создаются два смешивающих сигнала (рис. 5.84), которые представляют собой последовательность двоичных данных, состояние которой зависит от того, какой бит необходимо скрыть в том или ином сегменте первичного сигнала.

"Единичный" и "нулевой" смешивающие сигналы умножаются на соответствующие им эхо-сигналы. Иными словами, последние масштабируются единицей или нулем на протяжении всего времени действия сигнала в зависимости от того, какой бит предусматривается поместить в любой из его отдельных сегментов. В дальнейшем два результата складываются друг с другом.

Необходимо заметить, что "нулевой" смешивающий сигнал представляет собой инверсию "единичного". Кроме этого, фронты переходов каждого из сигналов являются наклонными. Сумма обоих смешивающих сигналов всегда равняется единице. Все это позволяет получить плавный переход между сегментами, кодированными разными битами, а также предотвращает возникновение резких изменений в звучании результирующего (смешанного) сигнала.

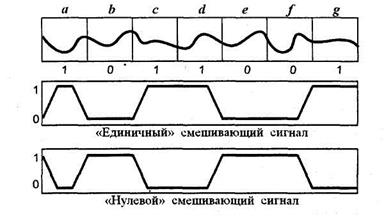
Рис. 5.84 Смешивающие сигналы

Блок-схема, которая отображает полный процесс встраивания, показана на рис. 5.85.

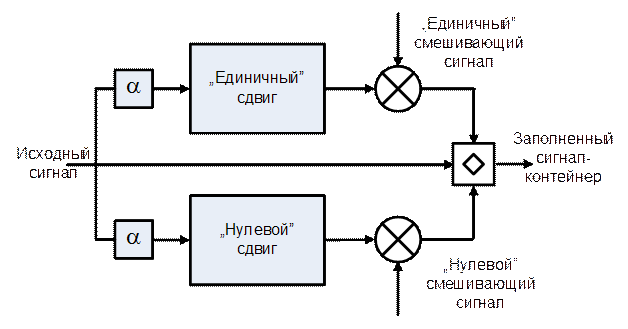
Рис. 5.85 Блок-схема встраивания информации методом эхо-сигнала

Извлечение вложенной информации подразумевает под собой выявление интервала между эхо-сигналами отдельных сегментов. Для этого необходимо исследовать в двух позициях амплитуду автокорреляционной функции (АКФ) косинус-преобразования Фурье натурального логарифма спектра мощности (или так называемого кепстра) кодированного сигнала [92,93]:

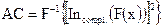(5.61)

Рассмотрим пример процесса извлечения, приведенный в [14]. Пусть получен закодированный сигнал, представляющий собой такую последовательность импульсов, в которой последние отделены друг от друга определенным интервалом и характеризуются экспоненциальным затуханием амплитуды. Во всех других точках сигнал равняется нулю (рис. 5.86).

Следующим шагом является поиск кепстра эхо-версии сигнала. Результат вычисления кепстра делает интервал между эхо-сигналом и первичным сигналом несколько более выраженным.

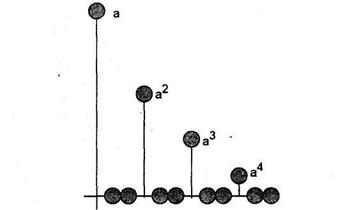
Рис. 5.86. Пример сигнала

К сожалению, результат вычисления кепстра кроме всего прочего дублирует эхо-сигнал через каждые 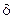секунд. На рис. 5.87 это изображено наличием последовательности импульсов на выходе. Более того, амплитуда импульсов, которые представляют эхо-сигнал, является малой по отношению к первичному сигналу. Как следствие, их трудно обнаружить

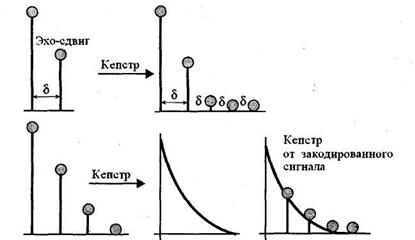
Рис. 5.87 Процесс получения кепстра от эхо-кодированного сигнала

Решение данной проблемы заключается в вычислении АКФ кепстра. С помощью однократного отображения сигнала с задержкой 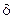(рис. 5.88), получаем результат, изображенный на рис. 5.89.

При этом значительно усилен только первый импульс, поскольку его "поддерживают" следующие за ним импульсы. Таким образом, в позиции первого импульса мы получаем всплеск. Подобно первому импульсу, всплеск повторяется через или же через секунд после всплеска первичного сигнала. Остаточные составляющие импульсов стремятся к нулю, что позволяет эффективно бороться с шумами.

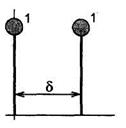
Рис. 5.88 Принцип отображения сигнала

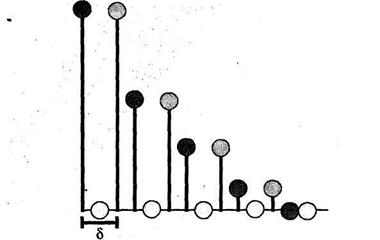
Рис. 5.89 Результат однократного отображения сигнала

Приведем критерий принятия решения относительно того, какой бит ("1" или "0") скрыт во временной задержке 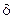всплеска АКФ по отношению к первичному сигналу. Вспомним, что "1" кодировалась размещением эхо-сигнала через 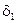, а "0" — через 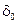секунд после оригинала. Аналогично при извлечении — бит является единичным, если значение АКФ через 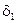секунд больше, чем через 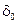секунд. В противном случае бит считается нулевым.

По утверждению авторов [14], с помощью данного метода вполне возможно скрывать/извлекать информацию в виде двоичного кода в/из потока аудиоданных с минимальным изменением первичного сигнала при пропускной способности, приблизительно, в 16 бит/с. Под минимальным изменением подразумевается тот факт, что среднестатистический человек не будет способен при этом почувствовать существенную разницу между модифицированным и первичным сигналами.

Однако; в другой своей работе [108] авторы указывают на то, что предложенный ими метод не является универсальным — для некоторых аудиосигналов невозможно получить достаточно высокий коэффициент правильно распознанных при извлечении бит даже при отсутствии помех в канале связи.

Рассмотрим реализацию метода эхо-кодирования с помощью системы Math-CAD.

Шаг1

Исходные данные: контейнер с частотой дискретизации f_Д=22050 Гц и количеством бит на один уровень квантования Q = 16:

C_total:= READWAV("C.wav") С := C_total^<1>; rows(C) = 20191.

Сообщение М:= "Опасность" длиной N_M := strlen(M), N_M= 9 символов или L_M:=8·NM,

L_M= 72бит.

Шаг 2

Пусть нулевая задержка между первичным и эхо-сигналом составляет 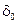:= 20 дискретных отсчетов (или 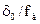= 0.907 мс), а единичная — 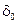:=30 отсчетов (или 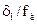= 1.361 мс).

"Единичный" и "нулевой" эхо-сигналы получим с помощью простого смещения на 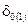отсчетов элементов контейнера-оригинала и поэлементного суммирования полученных векторов (предварительно умноженных на коэффициент затухания 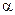а) с вектором С — программные модули (М.122) и (М.123).

Фрагменты (первые 70 отсчетов) результата сдвига сигнала С на 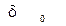и 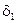, отсчетов изображены на рис. 5.90.

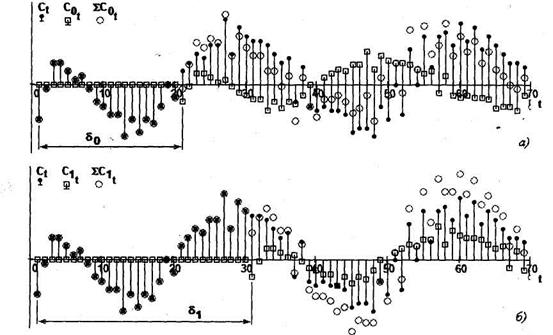
Рис. 5.90 "Нулевой" и "единичный" эхо-сигналы массива С при параметре

Шаг 3

Для возможности скрытия более одного бита первичный сигнал С необходимо разделить на меньшие сегменты, каждый из которых будет рассматриваться как отдельный сигнал и в который путем эхо-отображения может быть встроен необходимый бит данных.

Вычислим количество отсчетов в одном сегменте, исходя из битовой длины сообщения L_M (путем округления к ближайшему наименьшему целому с помощью функции floor( )):

N_Б :=floor(rows(C)/L_M), N_Б=280

Шаг 4

Исходя из указанной при описании метода необходимости в наклонных фронтах импульсов смесительных сигналов (трапецеидальные импульсы), предварительно задаемся следующим:

• размах импульса: U:= 1;

• длительность фронтов: 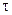:= 20 отсчетов;

• длительность импульса по уровню U: Т := N_Б - х, Т = 260 отсчетов;

Амплитуды отсчетов импульса формируем с помощью комплексного программного модуля (М.124).

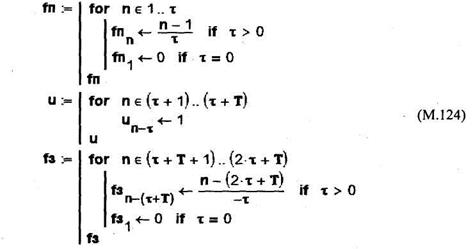
Графическая интерпретация вычисления модуля (М.124) приведена на рис. 5.91.

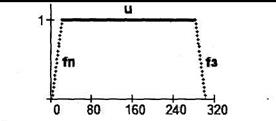
Рис. 5.91 Трапецеидальный импульс, построенный по 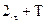отсчетам

Формирование смесительных сигналов выполним, пользуясь программным модулем (М.125). При этом принимаем, что каждый бит сообщения кодируется половиной переднего фронта импульса, его единичным уровнем и половиной заднего фронта.

После формирования смесительного сигнала для всех L_M бит сообщения, данный сигнал дописывается нулевым или единичным уровнем, в зависимости от значения последнего (L_M -го) бита. Нулевой смесительный сигнал получается из единичного с учетом того, что их сумма должна равняться единице.

Смесительные сигналы для первой восьмерки бит сообщения представлены на рис. 5.92.

Рис. 5.92 "Нулевой" 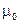и "единичный" 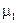смесительные сигналы

Шаг 5

Непосредственно встраивание бит сообщения в аудиоконтейнер выполняет программный модуль (МЛ 26).

В зависимости от значения текущего бита бинарного сообщения M_{vec_bin}, проводится выделение сегмента заданной размерности (N_Б) из соответствующего эхо-сигнала ( 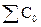или 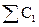) и из смесительного сигнала ( 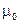или 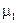), которые в дальнейшем поэлементно перемножаются (для чего можно также использовать и операцию векторизации).

Полученные для каждого бита векторы s' формируют общий вектор заполненного контейнера S, в конец которого после встраивания последнего символа сообщения дописываются элементы контейнера-оригинала, которые не были модифицированы. Очевидно, что количество элементов сформированного вектора S будет отвечать соответствующему показателю для вектора С, то есть rows(S) = 20191.

Полученный вектор объединяем с немодифицированным вторым каналом, а результат объединения записываем в аудиофайл:

WRITEWAV ("S_echo.wav", f_Д, Q) := augment(S, C_total^<1>)

Шаг 6

Для извлечения скрытого сообщения предусматривается следующее: получателю известны размерность блоков, на которые разбивается контейнер (то есть 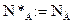), а также значения нулевой и единичной задержек ( ).

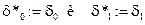Программный модуль извлечения данных — (М.127). В основу модуля положено вычисление автокорреляционной функции кепстра (5.61), однако для более надежного извлечения анализируется окрестность отсчетов 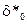и .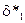

На pис. 5.93 приведен результат вычисления АКФ кепстра для первого и восьмого бит сообщения .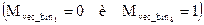

Результаты вычисления показателей звукового искажения контейнера при внесении в него данных путем эхо-кодирования .сведены в табл. 5.6.

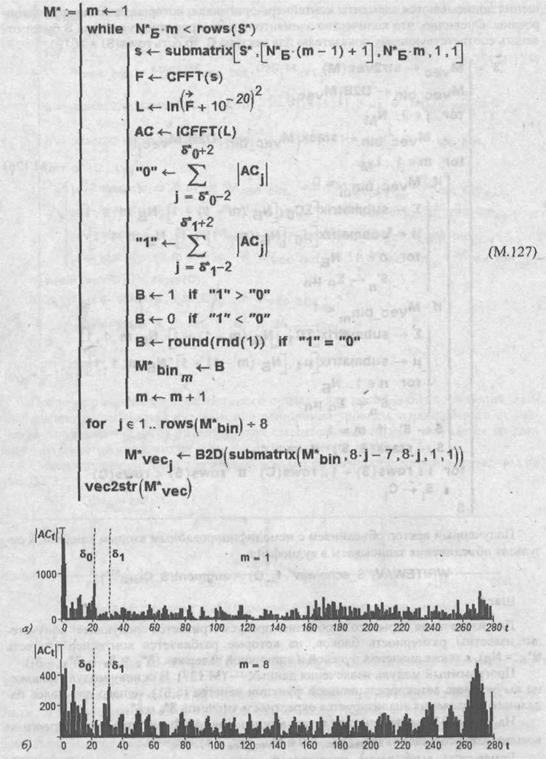
Рис. 5.93. Пример вида АКФ кепстра сигнала, который содержит "нулевое" (а) и "единичное" (б) эхо-отображение

Таблица 5.6. Показатели звукового искажения в случае скрытия данных в аудиосреде

Название показателя искажения	Оригинал	Методы скрытия данных в аудиосреде
НЗБ (ПС интервал)	Фазовое кодирование	Расширение спектра	Эхо-кодирование
Максимальная разность, MD
Средняя абсолютная разность, AD		3.244·10-3	15.298	14.321	572.093
Нормированная средняя абсолютная разность, NAD		2.625·10-6	0.012	0.012	0.5
Среднеквадратическая ошибка, MSE		0.003	2.657 ·103	956.742	7.640· 105
Нормированная среднеквадратическая ошибка, NMSE		9.402· 10-10	7.702·10-4	2.773·10-4	0.250
Lp- норма, р = 2		0.057	51.551	30.931	874.01
Отношение "сигнал/шум", SNR	∞	1.064·109	1.298·103	3.606·103	4.006
Максимальное отношение "сигнал/шум", PSNR	∞	1.177·1010	1.437·104	3.992·104	45.968
Качество звучания, AF		≈1	0.999230	0.999723	0.750371
Нормированная взаимная корреляция, NC		≈1	0.999615	0.999806	1.255078
Качество корреляции, CQ	2.792·103	2.792·103	2.790·103	2.791·103	3.355·103
Структурное содержание, SC		≈1	≈1	1.000110	0.568251
Общее сигма-отношение "сигнал/шум", GSSNR	∞	1.152·1014	1.51·1020	3.279·108	9.377
Сигма-отношение "сигнал/шум", SSNR	∞	140.6	201.8	85.2	9.721
Отношение "сигма/ошибка", SER	∞	1.064-109	1.298-103	3.606- 103	4.006
Подобие гистограмм. HS

Скрытие данных в тексте

Для скрытия конфиденциальных сообщений в тексте (так называемая лингвистическая стеганография) используется или обычная избыточность письменной речи, или же форматы представления текста.

Наиболее сложным объектом для скрытия данных по многим причинам является электронная (файловая) версия текста. В отличие от текстового файла его "жесткая" копия (например, бумажная) может быть обработана как высокоструктурированное изображение и поэтому является относительно легко поддающейся разнообразным методам скрытия, таким как незначительные изменения формата текстовых шаблонов, регулирование расстояния между определенными парами символов (кернинг), расстояния между строками и т.п. В значительной степени такая ситуация вызвана относительным дефицитом в текстовом файле избыточной информации, особенно в сравнении с графическими или, например, звуковыми файлами. В то время как в большинстве случаев существует возможность внести незаметные глазу и неощутимые на слух модификации в изображение и звук, даже дополнительная буква или знак пунктуации в тексте могут быть легко распознаны случайным читателем.

Скрытие данных в тексте требует поиска таких модификаций, которые были бы незаметными подавляющему большинству читателей. Авторы [14] рассматривают три группы методов, которые получили наибольшее распространение при встраивании скрываемых данных в текст:

• методы произвольного интересна, которые осуществляют встраивание путем манипуляции с пробельными символами (свободным местом на печатной полосе);

• синтаксические методы, которые работают с пунктуацией;

• семантические методы, в основу алгоритмов которых положено манипулирование словами, зависимое от скрываемых бит данных.