Методика кластерного анализа

Кластерный анализ (КлА)– это совокупность методов многомерной классификации, целью которой является образование групп (кластеров) схожих между собой объектов. В отличие от традиционных группировок, рассматриваемых в общей теории статистики, КлА приводит к разбиению на группы с учетом всех группировочных признаков одновременно.

Методы КлА позволяют решать следующие задачи:

- проведение классификации объектов с учетом множества признаков;

- проверка выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности объектов, т.е. поиск существующей структуры;

- построение новых классификаций для слабо изученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.

Для записи формализованных алгоритмов КлА используются следующие условные обозначения:

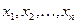– совокупность объектов наблюдения;

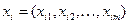– i-е наблюдение в m-мерном пространстве признаков ( );

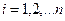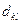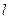– расстояние между -м и -м объектами;

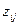– нормированные значения исходных переменных;

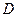– матрица расстояний между объектами.

Для реализации любого метода КлА необходимо ввести понятие «сходство объектов». Причем в процессе классификации в каждый кластер должны попадать объекты, имеющие наибольшее сходство друг с другом с точки зрения наблюдаемых переменных.

Для количественной оценки сходства вводится понятие метрики. Каждый объект описывается -признаками и представлен как точка в -мерном пространстве. Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. Как правило, используются следующие меры расстояния между объектами:

- евклидово расстояние ;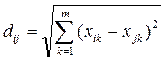

- взвешенное евклидово расстояние ;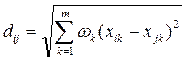

- расстояние city-block ;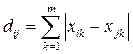

- расстояние Махаланобиса ,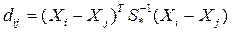

где 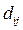– расстояние между -ым и 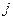-ым объектами;

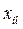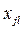, – значения 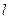-переменной и соответственно у -го и 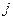-го объектов;

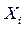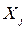, – векторы значений переменных у -го и -го 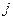объектов;

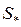– общая ковариационная матрица;

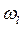– вес, приписываемый 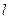-й переменной.

Все методы КлА можно разделить на две группы: иерархические (агломеративные и дивизимные) и итеративные (метод -cpeдних, метод поиска сгущений).

Иерархический кластерный анализ. Из всех методов кластерного анализа наиболее распространенными является агломеративный алгоритм классификации. Сущность аглогритма заключается в том, что на первом шаге каждый объект выборки рассматривается как отдельный кластер. Процесс объединения кластеров происходит последовательно: на основании матрицы расстояний или матрицы сходства объединяются наиболее близкие объекты. Если матрица расстояний первоначально имеет размерность ( ), то полностью процесс объединения завершается за ( 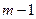) шагов. В итоге все объекты будут объединены в один кластер.

Последовательность объединения может быть представлена в виде дендрограммы, представленной на рисунке 3.1. Дендрограмма показывает, что на первом шаге объединены в один кластер второй и третий объекты при расстоянии между ними 0,15. На втором шаге к ним присоединился первый объект. Расстояние от первого объекта до кластера, содержащего второй и третий объекты, 0,3 и т.д.

Множество методов иерархического кластерного анализа отличаются алгоритмами объединения (сходства), из которых наиболее распространенными являются: метод одиночной связи, метод полных связей, метод средней связи, метод Уорда.

Метод полных связей – включение нового объекта в кластер происходит только в том случае, если сходство между всеми объектами не меньше некоторого заданного уровня сходства (рисунок 1.3).

	б)

Метод средней связи – при включении нового объекта в уже существующий кластер вычисляется среднее значение меры сходства, которое затем сравнивается с заданным пороговым уровнем. Если речь идет об объединении двух кластеров, то вычисляют меру сходства между их центрами и сравнивают ее с заданным пороговым значением. Рассмотрим геометрический пример с двумя кластерами (рисунок 1.4).

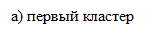
Рисунок 1.4. Объединение двух кластеров по методу средней связи:

Если мера сходства между центрами кластеров ( 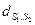) будет не меньше заданного уровня, то кластеры 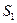и 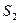будут объединены в один.

Метод Уорда – на первом шаге каждый кластер состоит из одного объекта. Первоначально объединяются два ближайших кластера. Для них определяются средние значения каждого признака и рассчитывается сумма квадратов отклонений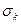

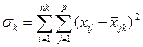, (1.1)

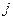где – номер кластера, – номер объекта, – номер признака; 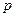– количество признаков, характеризующих каждый объект; – количество объектов в -мкластере.

В дальнейшем на каждом шаге работы алгоритма объединяются те объекты или кластеры, которые дают наименьшее приращение величины .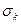

Метод Уорда приводит к образованию кластеров приблизительно равных размеров с минимальной внутрикластерной вариацией.

Алгоритм иерархического кластерного анализа можно представить в виде последовательности процедур:

- нормирование исходных значений переменных;

- расчет матрицы расстояний или матрицы мер сходства;

- определение пары самых близких объектов (кластеров) и их объединение по выбранному алгоритму;

- повторение первых трех процедур до тех пор, пока все объекты не будут объединены в один кластер.

Мера сходства для объединения двух кластеров определяется следующими методами:

- метод «ближайшего соседа» – степень сходства между кластерами оценивается по степени сходства между наиболее схожими (ближайшими) объектами этих кластеров;

- метод «дальнего соседа» – степень сходства оценивается по степени сходства между наиболее отдаленными (несхожими) объектами кластеров;

- метод средней связи – степень сходства оценивается как средняя величина степеней сходства между объектами кластеров;

- метод медианной связи – расстояние между любым кластером S и новым кластером, который получился в результате объединения кластеров р и q, определяется как расстояние от центра кластера S до середины отрезка, соединяющего центры кластеров р и q.

Метод поиска сгущений. Одним из итеративных методов классификации является алгоритм поиска сгущений. Суть итеративного алгоритма данного метода заключается в применении гиперсферы заданного радиуса, которая перемещается в пространстве классификационных признаков с целью поиска локальных сгущений объектов.

Метод поиска сгущений требует, прежде всего, вычисления матрицы расстояний (или матрицы мер сходства) между объектами и выбора первоначального центра сферы. Обычно на первом шаге центром сферы служит объект (точка), в ближайшей окрестности которого расположено наибольшее число соседей. На основе заданного радиуса сферы (R) определяется совокупность точек, попавших внутрь этой сферы, и для них вычисляются координаты центра (вектор средних значений признаков).

Когда очередной пересчет координат центра сферы приводит к такому же результату, как и на предыдущем шаге, перемещение сферы прекращается, а точки, попавшие в нее, образуют кластер, и из дальнейшего процесса кластеризации исключаются. Перечисленные процедуры повторяются для всех оставшихся точек. Работа алгоритма завершается за конечное число шагов, и все точки оказываются распределенными по кластерам. Число образовавшихся кластеров заранее неизвестно и сильно зависит от радиуса сферы.

Для оценки устойчивости полученного разбиения целесообразно повторить процесс кластеризации несколько раз для различных значений радиуса сферы, изменяя каждый раз радиус на небольшую величину.

Существуют несколько способов выбора радиуса сферы. Если 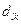– расстояние между 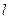-м и -м объектами, то в качестве нижней границы радиуса ( 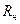)выбирают 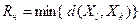, а верхняя граница радиуса 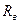может быть определена как .

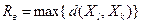Если начинать работу алгоритма с величины 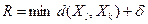и при каждом его повторении изменять 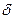на небольшую величину, то можно выявить значения радиусов, которые приводят к образованию одного и того же числа кластеров, т.е. к устойчивому разбиению.

Пример 1. На основании приведенных данных таблицы 1.1 необходимо провести классификацию пяти предприятий при помощи иерархического агломеративного кластерного анализа.

Таблица 1.1

Номер предприятия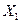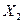
	220,0 185,0 245,0 178,0 170,0	94,0 75,0 80,0 75,2 73,1	264,0 192,0 220,0 96,0 105,0
Среднее значение ( 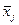)	199,6	79,5	175,4
Среднее квадратическое отклонение ( 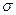)	28,4	7,6	65,4

Здесь: 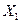– среднегодовая стоимость основных производственных фондов, млрд. р.; 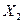– материальные затраты на один рубль произведенной продукции, коп.; – объем произведенной продукции, млрд. р.

Решение. Перед тем как вычислять матрицу расстояний, нормируем исходные данные по формуле

.

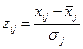Матрица значений нормированных переменных будет иметь вид

.

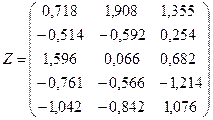Классификацию проведем при помощи иерархического агломеративного метода. Для построения матрицы расстояний воспользуемся евклидовым расстоянием. Тогда, например, расстояние между первым и вторым объектами будет

.

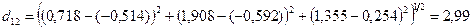Матрица расстояний 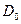характеризует расстояния между объектами, каждый из которых, на первом шаге представляет собой отдельный кластер

.

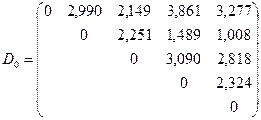Как видно из матрицы 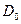, наиболее близкими являются объекты 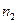и 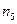. Объединим их в один кластер и присвоим ему номер 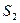. Пересчитаем расстояния всех оставшихся объектов (кластеров) до кластера 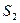получим новую матрицу расстояний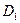

.

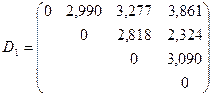В матрице 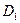расстояния между кластерами определены по алгоритму «дальнего соседа». Тогда расстояние между объектом 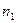и кластером 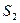равно

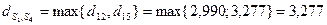и т.д.

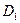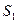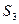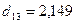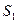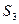В матрице опять находим самые близкие кластеры. Это будут и , . Следовательно, на этом шаге объединяем и кластеры; получим новый кластер, содержащий объекты 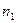, 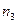. Присвоим ему номер 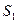. Теперь имеем три кластера 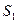{1,3}, 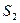{2,5}, 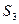{4}.

.

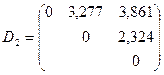Судя по матрице 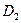,на следующем шаге объединяем кластеры 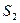и 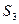, 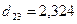в один кластер и присвоим ему номер 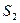. Теперь имеем только два кластера:

.

.

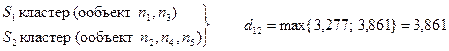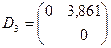И, наконец, на последнем шаге объединим кластеры 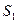и 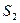на расстоянии 3,861.

Представим результаты классификации в виде дендрограммы (рисунок 1.5). Дендрограмма свидетельствует о том, что кластер 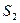более однороден по составу входящих объектов, так как в нем объединение происходило при меньших расстояниях, чем в кластере .

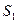Рисунок 3.5.Дендрограмма кластеризации пяти объектов

Пример 2. На основании данных, приведенных ниже, проведите классификацию магазинов по трем признакам: 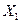– площадь торгового зала, м² , 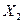– товарооборот на одного продавца, ден. ед., – уровень рентабельности, %.

Номер магазина		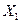		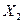Номер магазина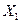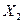

Для классификации магазинов используйте метод поиска сгущений (необходимо выделить первый кластер).

Решение. 1. Рассчитаем расстояния между объектами по евклидовой метрике

,

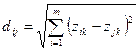где 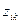, – стандартизированные значения исходных переменных соответственно у -го и 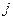-го объектов; т – число признаков.

.

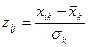
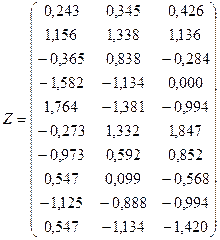2. На основе матрицы Z рассчитаем квадратную симметричную матрицу расстояний между объектами ( ).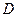

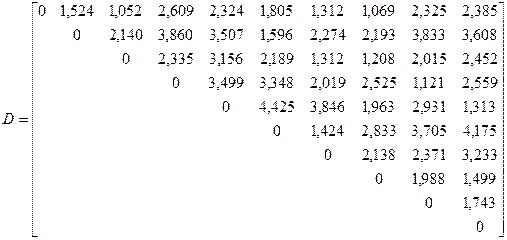
Анализ матрицы расстояний помогает определить положение первоначального центра сферы и выбрать радиус сферы.

В данном примере большинство «маленьких» расстояний находятся в первой строке, т.е. у первого объекта достаточно много «близких» соседей. Следовательно, первый объект можно взять в качестве центра сферы.

3. Зададим радиус сферы 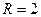. В этом случае в сферу попадают объекты, расстояние которых до первого объекта меньше 2.

, , , , .

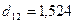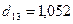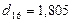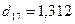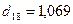Для шести точек (объекты 1, 2, 3, 6, 7, 8) определяем координаты центра тяжести: .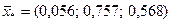

4. На следующем шаге алгоритма помещаем центр сферы в точку 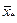и определяем расстояние каждого объекта до нового центра:

.

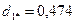
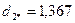
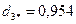
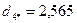
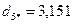
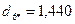
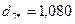
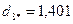
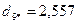
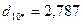Следовательно, в сферу опять попали объекты 1, 2, 3, 6, 7, 8, расстояния которых до центра меньше радиуса сферы. Поскольку в этом случае центр сферы не изменит своих координат, выделение первого кластера закончено, в его состав вошли шесть объектов (1,2,3,6,7,8).

5. Чтобы начать формирование второго кластера, нужно поместить центр сферы в одну из точек, не вошедших в первый кластер (объекты 4,5,9,10).

Судя по матрице расстояний 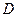, целесообразно в качестве центра сферы выбрать объекты 9 или 10. Если взять объект 9 в качестве центра сферы, то в сферу попадают четыре точки (объекты 4,8,9,10). Рассчитаем для них координаты нового центра тяжести .

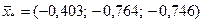6. Определим расстояние каждого из десяти объектов до точки :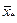

.

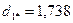
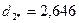
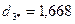
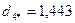
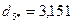
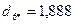
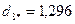
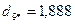
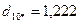В сферу попадают объекты, которые имеют расстояние до центра 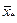меньше двух (объекты 1,3,4,8,9,10).

На основании матрицы Z по евклидовой метрике определяем новые координаты центра для этих точек .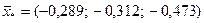

Для нового центра повторяем пункт 6 данного алгоритма:

.

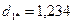
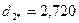
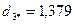
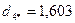
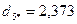
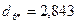
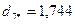
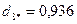
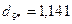
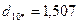После выполнения этого шага видно, что в сферу с радиусом R=2 попадают объекты 1,3,4,7,8,9,10, т.е. состав второго кластера опять изменился. Следовательно, повторяются процедуры пункта 6 и пункта 7:

.

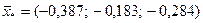
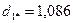
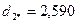
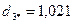
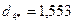
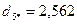
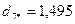
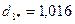
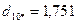Как видно из полученных расстояний каждого из десяти объектов до центра второго кластера, состав кластера не изменился. На этом выделение второго кластера завершается. В его состав вошли семь объектов 1,3,4,7,8,9,10.

Второй кластер

Первый кластер

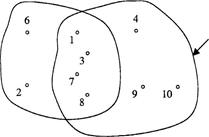Результаты выделения первых двух кластеров представлены на рисунке 3.6

Так как полученные кластеры являются пересекающимися и в области пересечения находятся четыре объекта из десяти, есть все основания считать результаты классификации неудовлетворительными. По-видимому, следует повторить классификацию, предварительно изменив радиус сферы или выбрать другой метод.