Представление чисел в двоичном коде. Дополнительный код

Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах — минимальных по размеру адресуемых (т.е. к ним возможно обращение) ячейках памяти. Очевидно, адресом числа следует считать адрес первого байта. В байте может содержаться произвольный код из восьми двоичных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число. Действительное число многообразно в своих «потребительских свойствах». Числа могут быть целые точные, дробные точные, рациональные, иррациональные, дробные приближенные, числа могут быть положительными и отрицательными. Числа могут быть «карликами», например, масса атома, «гигантами», например, масса Земли, реальными, например, количество студентов в группе, возраст, рост. И каждое из перечисленных чисел потребует для оптимального представления в памяти свое количество байтов. Очевидно, единого оптимального представления для всех действительных чисел создать невозможно, поэтому создатели вычислительных систем пошли по пути разделения единого по сути множества чисел на типы (например, целые в диапазоне от ... до ..., приближенные с плавающей точкой с количеством значащих цифр ... и т.д.). Для каждого в отдельности типа создается собственный способ представления.

Целые числа.

Целые положительные числа от 0 до 255 можно представить непосредственно в двоичной системе счисления (двоичном коде). Такие числа будут занимать один байт в памяти компьютера.

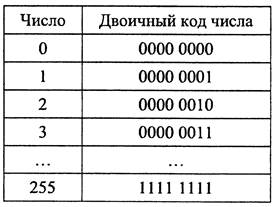
В такой форме представления легко реализуется на компьютерах двоичная арифметика.

Если нужны и отрицательные числа, то знак числа может быть закодирован отдельным битом, обычно это старший бит; ноль интерпретируется как плюс, единица как минус. В таком случае одним байтом может быть закодированы целые числа в интервале от —127 до +127. Рассмотренный способ представления целых чисел называется прямым кодом. Положение с отрицательными числами несколько упрощается, если использовать, так называемый, дополнительный код. В дополнительном коде положительные числа совпадают с положительными числами в прямом коде, отрицательные же числа получаются в результате инверсии всех битов числа и добавлении единицы к младшему левому разряду. Например, число 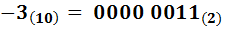получит код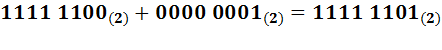

При представлении отрицательных чисел в дополнительном коде операция вычитания заменяется операцией сложения. Например,

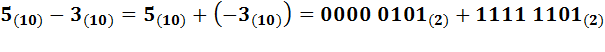
Отбрасывая подчеркнутый старший разряд, получим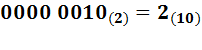

Действительные числа. Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Однако в ЭВМ числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в ЭВМ выступают как приближенные.

Для представления действительных чисел большой и малой разрядности удобно использовать форму записи чисел в виде произведения

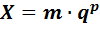
где 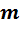- мантисса числа;

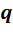- основание системы счисления;

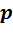- целое число, называемое порядком.

Такой способ записи чисел называется представлением числа с плавающей запятой. Число 4235,25 может быть записано в одном из видов:

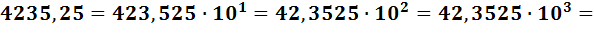
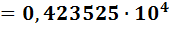
Если мантисса для десятичной системы счисления

,

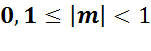либо же для двоичной

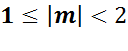
то представление числа становится однозначным, а такая форма называется нормализованной. Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т.е. максимальная точность.

Действительные числа в ЭВМ различных типов записываются по-разному, тем не менее существует несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру. Рассмотрим на примере числа, занимающего 4 байта.

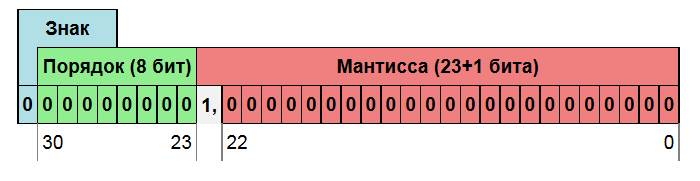
Первый бит двоичного представления используется для кодирования знака мантиссы. Следующая группа бит кодирует порядок числа, а оставшиеся биты кодируют абсолютную величину мантиссы. Длины порядка и мантиссы фиксированы.

Порядок числа – целые числа, могут быть как положительными, так и отрицательными. Чтобы отразить в двоичной форме, величина порядка представляется в виде суммы истинного порядка и константы, равной абсолютной величине максимального по модулю отрицательного порядка, называемой смещением. Например, если порядок может принимать значения от —128 до 127 (8 бит), тогда, выбрав в качестве смещения 128, можно представить диапазон значений порядка от 0 (-128+128, порядок + смещение) до 255 (127+128).

Так как мантисса нормализованного числа всегда начинается с нуля, некоторые схемы представления его лишь подразумевают, используя лишний разряд для повышения точности представления мантиссы. Использование смещенной формы позволяет производить операции над порядками как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, пред ставимого в компьютере при заданном формате.

Вещественные числа в памяти компьютера, в зависимости от требуемой точности (количества разрядов мантиссы) и диапазона значений (количества разрядов порядка), занимают от четырех до десяти байтов. Например, четырехбайтовое вещественное число имеет 23 разряда мантиссы (что соответствует точности числа 7—8 десятичных знаков) и 8 разрядов порядка (обеспечивающих диапазон значений 10±38). Если вещественное число занимает десять байтов, то мантиссе отводится 65 разрядов, а порядку — 14 разрядов. Это обеспечивает точность 19—20 десятичных знаков мантиссы и диапазон значений 10±4931.

Число двойной точности (для 32-разрядны ЭВМ – 64 бита или 8 байт)

Понятие типа данных

Как уже говорилось, минимально адресуемой единицей памяти является байт, но представление числа требует большего объема. Очевидно, такие числа займут группу байт, а адресом числа будет адрес первого байта группы. Следовательно, произвольно взятый из памяти байт ничего нам не скажет о том, частью какого информационного объекта он является — целого числа, числа с плавающей запятой или команды. Резюмируя вышесказанное, можно сделать вывод, что кроме задачи представления данных в двоичном коде, параллельно решается обратная задача — задача интерпретации кодов, т.е. как из кодов восстановить первоначальные данные. Для представления основных видов информации (числа целые, числа с плавающей запятой, символы, звук и т.д.) в системах программирования используют специального вида абстракции — типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных. В дальнейшем для каждого типа данных будут определены и соответствующие ему операции обработки.