Дифракционная решетка как спектральный прибор

Дифракционные решетки создают эффект резкого разделения и усиления интенсивности света в области максимумов, что делает их незаменимыми оптическими приборами. Они позволяют получать ярко выраженную дифракционную картину.

Положение дифракционных максимумов зависит от длины волны света 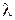(из формулы (11.2а) следует 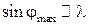). Поэтому при пропускании через решётку белого света, все максимумы кроме центрального разложатся в спектр, фиолетовый конец которого направлен к центру дифракционной картины, а красный наружу. Таким образом, дифракционная решётка представляет собой спектральный прибор.

При освещении щели белым светом, центральный максимум наблюдается в виде белой полоски (потому, что при 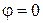разность хода равна нулю для всех 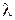) — он общий для всех длин волн. Боковые максимумы радужно окрашены фиолетовым краем к центру дифракционной картины (поскольку < 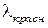), в отличие от дисперсии в призме.

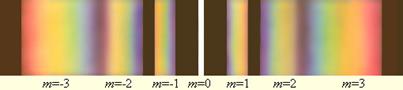
Рис. 14. 1.

Таким образом, картина дифракции Фраунгофера белого света на щели будет представлять собой центральную светлую полоску и ряд минимумов и максимумов, расположенных по обе стороны от неё в направлении перпендикулярном направлению щели.

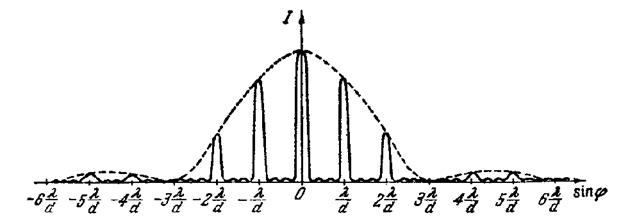
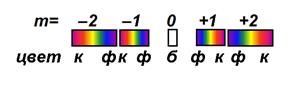
Рис. 14.2

В центре дифракционной картины лежит узкий максимум нулевого порядка; у него окрашены только края. По обе стороны от центрального максимума расположены два спектра 1-го порядка, затем два 2-го порядка и т.д. Начиная со второго порядка, происходит частичное перекрытие спектров 2-го и 3-го порядков, 3-го и 4-го порядков и т.д. Поэтому дифракционная решетка может быть использована как спектральный прибор для разложения света в спектр и измерения длин волн.

Поскольку в условии главных максимумов (11.2а) 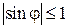, то максимальное число главных максимумов, даваемое дифракционной решеткой:

(14.1)

Угловая ширина центрального (нулевого) главного максимума на рис. 11.2 и рис. 14.2 определяется формулой

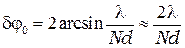(14.2)

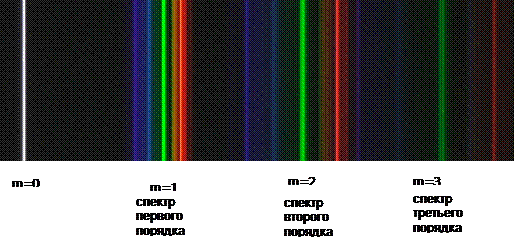
Рис. 14.3. Дифракционный спектр люминесцентной лампы (показана только
правая половина спектра)

Основными характеристиками любого спектрального прибора являются угловая дисперсия, разрешающая способность и область дисперсии, рассмотрим их.

Угловая дисперсия

Угловой дисперсией называется величина

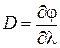(14.3)

Чтобы найти угловую дисперсию дифракционной решётки, продифференцируем левую часть условие главного максимума по углу 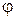, а правую по 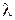. Опуская знак минус в левой части, получим:

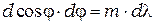
Отсюда:

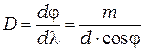. (14.4)

При малых углах дифракции 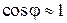, поэтому можно положить

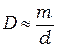(14.5)

Из полученного выражения следует, что угловая дисперсия обратно пропорциональна периоду решётки 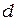. Чем выше порядок спектра 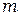, тем больше дисперсия.

Линейной дисперсией называют величину

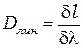, (14.6)

где 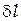- линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на 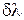. Из рис. 4.14 видно, что при небольших значениях углах 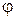можно положить 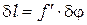, где 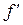- фокусное расстояние линзы, собирающей дифрагирующие луч на экране.

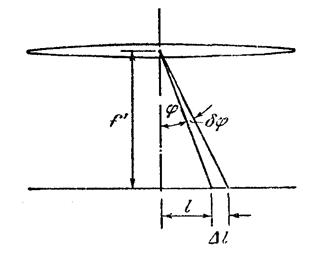
Рис. 14.4

Следовательно, линейная дисперсия связана с угловой дисперсией 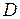соотношением

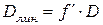
Или приняв во внимание (14.5)

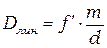(14.7)

Разрешающая способность

По определению разрешающей способностью называется величина

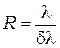(14.8)

где 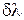— наименьшая разность длин волн спектральных линий, при которой эти линии воспринимаются еще раздельно, т. е. разрешаются. Величина 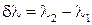не может быть по ряду причин определена точно, а лишь ориентировочно (условно). Такой условный критерий был предложен Рэлеем.

Согласно критерию Рэлея, спектральные линии с разными длинами волн, но одинаковой интенсивности, считаются разрешёнными, если главный максимум одной спектральной линии совпадает с первым минимумом другой (рис. 16).

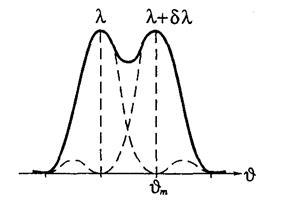
Рис. 14.5

Найдем разрешающую силу дифракционной решетки. Положение середины 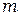-го максимума для длины волны определяется условием:

Края 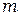максимума для длины волны 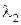расположены под углами, удовлетворяющими соотношению:

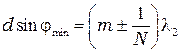
Середина максимума для длины волны ( 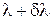) наложится на край максимума для длины волны в том случае, если:

,

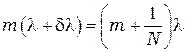откуда

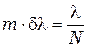
Решая это соотношение относительно , находим

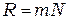(15.27)

В этом случае между двумя максимумами возникает провал, составляющий около 20%от интенсивности в максимумах, и линии еще воспринимаются раздельно

Это и есть искомая формула для разрешающей способностидифракционной решётки. данная формула дает верхний предел разрешающей способности. Она справедлива при выполнении следующих условий:

1. Интенсивность обоих максимумов должна быть одинаковой.

2. Расширение линий должно быть обусловлено только дифракцией.

3. Необходимо, чтобы падающий на решётку свет имел ширину когерентности, превышающую размер решетки. Только в этом случае все 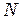штрихов решётки будут «работать» согласованно (когерентно), и мы достигнем желаемого результата.

Для повышения разрешающей способности спектральных приборов можно, как показывает формула (15.27),либо увеличивать число 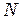когерентных пучков, либо повышать порядок интерференции .

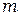Первое используется в дифракционных решетках (число 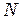доходит до 200 000),второе - в интерференционных спектральных приборах (например, в интерферометре Фабри-Перо число 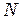интерферирующих волн невелико, порядка нескольких десятков, а порядки интерференции 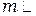10⁶ и более).

Область дисперсии

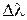— это ширина спектрального интервала, при которой еще нет перекрытия спектров соседних порядков. Если спектры соседних порядков перекрываются, то спектральный аппарат становится непригоднымдля исследования соответствующего участка спектра. длинноволновый конец спектра 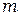-го порядка совпадает с коротковолновым концом спектра -го порядка, если 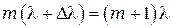, откуда следует, что область дисперсии

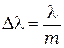(5.33)

Значит, область дисперсии 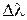обратно пропорциональна порядку спектра 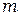. При работе со спектрами низких порядков (обычно второго или третьего) дифракционная решетка пригодна для исследования излучения, занимающего достаточно широкий спектральный интервал. В этом главное преимущество дифракционных решеток перед интерференционными спектральными приборами, например, интерферометром Фабри - Перо, у которого из-за высоких порядков 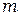область дисперсии очень мала.

Еще о дифракционных решётках. Дифракционная решётка является одним из важнейших спектральных приборов, которому наука обязана многими фундаментальными открытиями. Спектр — это по существу код, который будучи расшифрован с помощью того или иного математического аппарата дает возможность получить ценнейшую информацию о свойствах атомов и внутриатомных процессов. Для адекватного решения этой задачи спектр должен быть неискажённым и чётко различимым — в этом суть той сложнейшей научно-технической проблемы, которую пришлось решить, чтобы наконец добиться получения высококачественных дифракционных решёток. Технология изготовления дифракционных решеток в настоящее время доведена до высокой степени совершенства. Первые высококачественные отражательные решётки были созданы в конце прошлого столетия Роулендом (США). О технической сложности решаемой проблемы говорит хотя бы уже такой факт, что необходимая для этой цели делительная машина создавалась в течение 20 лет! Его дело продолжили Андерсен, Вуд и другие знаменитые экспериментаторы.

Современные полностью автоматизированные делительные машины позволяют с помощью алмазного резца изготовлять решётки с почти строго эквидистантным расположением штрихов. Трудно даже представить, что алмазный резец при этом прочерчивает десятки километров, практически не изменяя свой профиль, — а это принципиально важно. Размеры уникальных решеток достигают 40х40 см! (Такие решетки используют в основном в астрофизике.) В зависимости от области спектра решётки имеют различное число штрихов на 1 мм: от нескольких штрихов, начиная с инфракрасной области, до 3600 — для ультрафиолетовой. В видимой области спектра 600 — 1200 штрих/мм. Ясно, что обращение с гравированной поверхностью таких решёток требует предельной осторожности.

Вследствие высокой стоимости оригинальных гравированных решёток получили распространение реплики, т. е. отпечатки гравированных решеток на специальных пластмассах, покрытых тонким отражательным слоем. По качеству реплики почти не уступают оригиналам. В 1970-х годах был разработан новый, голографический метод изготовления дифракционных решёток. В этом методе плоская подложка со светочувствительным слоем освещается двумя плоскими наклонными пучками когерентных лазерных излучений с определенной длиной волны. В области пересечения пучков образуется стационарная интерференционная картина с синусоидальным распределением интенсивности. После соответствующей обработки светочувствительного слоя получается качественная дифракционная решетка.

Отметим в заключение, что, кроме прозрачных и отражательных решёток, существуют ещё и фазовые. Они влияют не на амплитуду световой волны, а вносят периодические изменения в её фазу. По этой причине их и называют фазовыми. Примером фазовой решетки может служить пластмассовая кювета с прозрачной жидкостью, в которой возбуждена плоская стоячая ультразвуковая волна. Это приводит к периодическому изменению плотности жидкости, а значит ее показателя преломления и оптической разности хода. Такая структура меняет не амплитуду проходящего поперек волны света, а только фазу. Фазовые решетки также находят многочисленные практические применения.

Одномерная решетка вибраторов. Аналогично дифракционной решётке ведет себя в радиодиапазоне система из 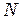параллельных друг другу вибраторов-антенн. Если они действуют синфазно, то нулевой (основной) максимум излучения направлен нормально к решетке в ее экваториальной плоскости. И здесь возникает интересная в практическом отношении возможность. Если создать режим, при котором колебания каждой следующей антенны будут, например, отставать по фазе от колебаний предыдущей на одну и ту же величину, то нулевой максимум не будет совпадать с нормалью к решетке. Изменяя же фазу во времени по определенному закону, мы получаем систему, у которой направление главного максимума будет изменяться в пространстве. Таким образом, мы приходим к возможности радиолокационного обзора местности с помощью неподвижной системы антенн.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ