Все перечисленные книги можно найти в интернете.
Дисциплина
ВЕРОТНОСТНО–СТАТИСТИЧЕСКИЕ МОДЕЛИ ЭКСПЛУАТАЦИИ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ»
Контрольная работа для студентов заочников, группа ЗМВ 156
Задача №1
Для графа состояний «замена по наработке», изображенном на рисунке 1, составить систему уравнений Колмогорова и найти финальные вероятности πiв каждом состоянии в соответствии с приведенными ниже вариантами. Общее условие для всех вариантов:
.
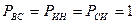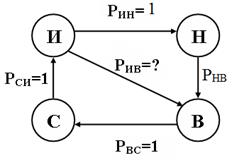
Рисунок 1
| № вар. | |||||||||||
| PИВ | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | 0,10 | 0,12 |
| № вар. | |||||||||||
| PИВ | 0,14 | 0,16 | 0,18 | 0,20 | 0,22 | 0,24 | 0,26 | 0,28 | 0,30 | 0,32 | 0,34 |
| № вар. | |||||||||||
| PИВ | 0,144 | 0,156 | 0,182 |
Задача №2
Эксплуатируется n изделий (самолетов). За какое-то время эксплуатации (например, между регламентами) выявлено, что вероятность отказа изделия (блока, прибора, элемента) равна p. Для указанных ниже вариантов определить:
1) математическое ожидание, дисперсию,коэффициент вариации числа отказавших изделий; 2) вероятность того, что все изделия будут исправны; 3) вероятность того, что все изделия будут неисправны; 4) вероятность того, что будет неисправно хотя бы одно изделие; 5) вероятность того, что будет неисправно ровно одно изделие; 6) вероятность того, что будет неисправно не более одного изделия.
| № вар. | |||||||||||
| P | 0.1 | 0.125 | 0.15 | 0.175 | 0.2 | 0.20 | 0.225 | 0.260 | 0.270 | 0.280 | 0.3 |
| n | |||||||||||
| № вар. | |||||||||||
| P | 0.3 | 0.4 | 0.25 | 0.250 | 0.285 | 0.090 | 0.35 | 0.375 | 0.250 | 0.325 | 0.190 |
| n | |||||||||||
| № вар. | |||||||||||
| P | 0.02 | 0.15 | 0.25 | ||||||||
| n |
Задание №3
Испытания надежности авиационной аппаратуры дали результаты, сформированные в корреляционную таблицу. В основной части таблицы – число опытов, закончившихся с результатами x, y , где x задает время наладки (испытания, доработки), y – время безотказной эксплуатации конкретного прибора. Используя МНК, определить коэффициенты для линии регрессии и записать уравнение линии регрессии в виде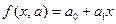 
, рассчитать коэффициент корреляции.
Вариант 1
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| nx |
Задача №4
Случайная величина Х подчиняется закону арксинуса с плотностью распределения
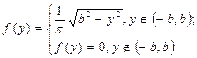
при b > 0 - параметр распределения. Найти функцию распределения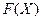 
.Вычислитьматематическое ожидание и дисперсию.
_______
Вариант 2
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | |||||
| - | ||||||
| - | ||||||
| - | ||||||
| nx |
Задача №4. Найти спектральную плотность стационарного случайного процесса, заданную своими спектральными разложением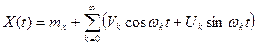 
.______________________________________________________
Вариант 3
Задача №1, 2 в таблицах
Задача №3.
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | |||||
| - | - | - | ||||
| nx |
Задача №4. Найти спектральную плотность вырожденного стационарного процесса X(t)(когда X(t)=V, где V – случайная величина), у которого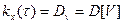 
.
___________
Вариант 4
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | |||||
| - | - | |||||
| - | - | - | - | |||
| - | - | - | - | |||
| nx |
Задача №4
Закон распределения амплитуд сигналов, отражённых от самолёта, по результатам различных экспериментов хорошо совпадает с распределением Релея: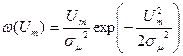 
Определить: a) математическое ожидание 
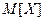; дисперсию 
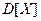; среднее квадратичное отклонение 
.
___________
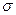Вариант 5
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | - | ||||
| nx |
Задача №4. Случайная величина Х подчиняется закону Релея с плотностью распределения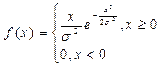 
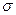, где >0 – параметр распределения. Найти функцию распределения 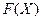. Вычислитьмат. ожидание и дисперсию.
Вариант 6
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | - | - | |||
| nx |
Задача №4
Случайная величина Х подчиняется закону арксинуса с плотностью распределения
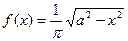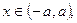
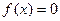при 
при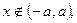 
при a>0-параметр .Найти функцию распределения 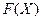.Вычислитьмат. ожидание, дисперсию.
_____________
Вариант 7
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| nx |
Задача № 4.Плотность вероятности случайной величины X имеет вид: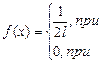 
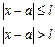
Определить математическое ожидание M[X], дисперсию D[X].
_____________
Вариант 8
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| nx |
Задача №4. Найти корреляцонную фунцию стационарного случайного процесса X(t), если ее спектральная плотность Sx(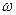 
) постоянна на интервале ( 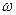1, 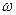2) и равна c, а вне этого интервала нулю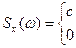 
.
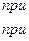
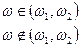Вариант 9
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | - | - | |||
| - | - | - | ||||
| nx |
Задача №4
Плотность вероятности случайных амплитуд изгибных колебаний крыльев самолетов имеет вид (закон Рэлея):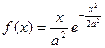 
(при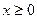 
).Определить: a) математическое ожидание 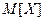; дисперсию 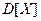; среднее квадратичное отклонение .
_____________
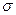Вариант 10
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| nx |
Задача №4
Найти спектральную плотность вырожденного стационарного процесса X(t)(когда X(t)=V, где V – случайная величина), у которого .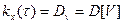
___________
Вариант 11
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | |||||
| - | ||||||
| - | ||||||
| - | ||||||
| nx |
Задача №4
Показать, что стационарный белый шум X(t) имеет постоянную спектральную плотность.
( 
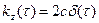, где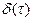 
– дельта функция ):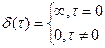 
Вариант 12
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | |||||
| - | ||||||
| - | ||||||
| - | ||||||
| nx |
Задача №4
Найти спектральную плотность случайного процесса X(t), представлящего собой случайную телеграфную волну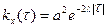 
.
____________
Вариант 13
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | ||||||
| nx |
Задача №4
Случайная величина Х подчиняется закону арксинуса с плотностью распределения
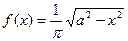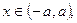
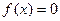при при 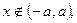n при a > 0 - параметр. Найти функцию распределения 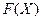.Вычислитьматематическое ожидание и дисперсию
_____________
Вариант 14
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | |||||
| - | - | |||||
| nx |
Задача №.Плотность вероятности случайной величины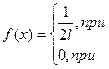 
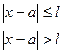
Определить математическое ожидание M[X], дисперсию D[X].
Вариант 15
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | |||||
| - | - | - | - | |||
| - | - | - | ||||
| nx |
Задача №4.
Найти спектральную плотность случайного процесса X(t), представлящего собой случайную телеграфную волну .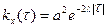
_____________
Вариант 16
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | - | - | |||
| - | - | - | ||||
| nx |
Задача №4
Найти спектральную плотность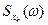 
элементарного случайного процесса 
.
_____________
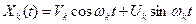Вариант 17
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | - | - | |||
| - | - | |||||
| nx |
Задача №4
Показать, что стационарный белый шум X(t) имеет постоянную спектральную плотность.
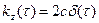( , где 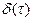– дельта функция ): .
_____________
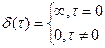Вариант 18
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | - | ||||
| - | - | |||||
| nx |
Задача №4. Плотность вероятности случайной величины X имеет вид: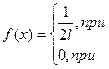
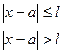
Определить математическое ожидание M[X], дисперсию D[X].
_____________
Вариант 19
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | - | ||||
| - | - | |||||
| nx |
Задача №4
Случайная величина Х подчиняется закону арксинуса с плотностью распределения
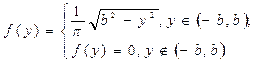
при b > 0 - параметр распределения. Найти функцию распределения 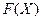.Вычислитьматематическое ожидание и дисперсию.
Вариант 20
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | - | |||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| nx |
Задача №4
Найти спектральную плотность случайного процесса X(t), представлящего собой случайную телеграфную волну .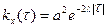
__________________
Вариант 21
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | ||||||
| nx |
Задача №4
Найти спектральную плотность стационарного случайного процесса, заданную своими спектральными разложением .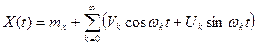
____________________
Вариант 22
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | ||||||
| nx |
Задача №4. Плотность вероятности случайной величины X: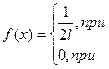
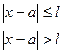
Определить математическое ожидание M[X], дисперсию D[X].
Вариант 23
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | - | |||
| - | - | |||||
| - | ||||||
| nx |
Задача №4Плотность вероятности случайной величины .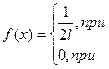
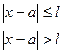Определить математическое ожидание M[X], дисперсию D[X].
________________
Вариант 24
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | ||||||
| nx |
Задача №4
Показать, что стационарный белый шум X(t) имеет постоянную спектральную плотность.
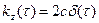( , где 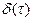– дельта функция ):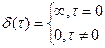
Вариант 25
Задача №1, 2 в таблицах
Задача №3
| X Y | ny | |||||
| - | - | - | ||||
| - | ||||||
| - | ||||||
| nx |
Задача №4.
Случайная величина Х подчиняется закону арксинуса с плотностью распределения
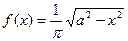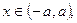
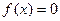при при 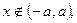n при a > 0 - параметр. Найти функцию распределения 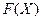.Вычислитьматематическое ожидание и дисперсию
Литература
1. Кабков П.К. Вероятнотно-статистические модели эксплуатации лететельных аппаратов: часть 2. – М, 2006. (Полумарковские процессы).
2. Кабков П.К. Вероятнотно-статистические модели эксплуатации лететельных аппаратов: пособие к практичеким занятиям – М, 2005.
3. Вентцель Е.С. Исследование операций: задачи, принципы, методология. –
М.,Наука,1988.
4. Вентцель Е.С., Овчаров Л.А. Задачи и упражения по теории вероятностей. – Учеб.пособие для втузов. – М.: Высш.шк.,2000.(Глава 2. Теорема сложения и умножения вероятностей, Глава 3. Формула полной вероятностии формула Бейеса, Глава 7. Стационарные случайные процессы)
5. Володин Б.Г., Ганин М.П., Свешников А.А и др. Сборник задач по теории вероятностей. Мтематической статистике и теории случайных функций. (Глава II. Случайные величины.)
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике.:Учеб. Пособие для студентов вузов. – М.: Высш.шк.,2000. (Часть 3. Глава 13.Элементы теории корреляции. Линейная корреляция., параграф 1).
7. Гмурман В.Е. Теория Вероятностей и математическая статистика.
.:Учеб. Пособие для вузов. – М.: Высш.шк.,1972. (Часть 3. Глава 18.Элементы теории корреляции. Корреляционная таблица., параграф 5; Метод четырех полей вычмсления выборочного коэффициента корреляции, параграф 8).
Все перечисленные книги можно найти в интернете.
Номер варианта по номеру в журнале.