Теоретико-множественные операции реляционной алгебры
Объединением двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно.
Пусть заданы два отношения R1 = { r1 } , R2 = { r2}, где r1 и r2 - соответственно кортежи отношений R1 и R2, то объединение
R1 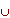 R2 = { r | r
R2 = { r | r  R1
R1 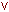 r
r  R2}.
R2}.
Здесь r — кортеж нового отношения, 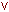 — операция логического сложения "ИЛИ".
— операция логического сложения "ИЛИ".
Пример применения операции объединения приведен ниже. Исходными отношениями являются отношения R1 и R2, которые содержат перечни деталей, изготавливаемых соответственно на первом и втором участках цеха. Отношение R3 содержит общий перечень деталей, изготавливаемых в цеху, то есть характеризует общую номенклатуру цеха.
| R1 | |
| Шифр детали | Название детали |
| Гайка M1 | |
| Гайка М2 | |
| Гайка М3 | |
| Болт М1 | |
| Болт М3 | |
| Шайба М1 | |
| Шайба М3 | |
| R2 | |
| Шифр детали | Название детали |
| Гайка M1 | |
| Гайка М3 | |
| Гайка М4 | |
| Болт М2 |
| R3 | |
| Шифр детали | Название детали |
| Гайка M1 | |
| Гайка М2 | |
| Гайка М3 | |
| Болт М1 | |
| Болт М3 | |
| Шайба М1 | |
| Шайба М3 | |
| Гайка М4 | |
| Болт М2 |
Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям. R1 и R2:
R3 = R1  R2 ={ r | r
R2 ={ r | r  R1
R1 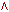 r
r  R2 }
R2 }
здесь 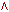 — операция логического умножения (логическое "И").
— операция логического умножения (логическое "И").
В отношении R4 содержится перечень деталей, которые выпускаются одновременно на двух участках цеха.
| R4 | |
| Шифр детали | Название детали |
| Гайка M1 | |
| Гайка М3 | |
| Болт М3 |
Разностью отношений R1 и R2 называется отношение, содержащее множество кортежей, принадлежащих R1 и не принадлежащих R2:
R5 =R1 \R2 ={r | r  R1
R1 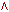 r
r  R2}
R2}
Отношение R5 содержит перечень деталей, изготавливаемых только на участке 1, отношение R6 содержит перечень деталей, изготавливаемых только на участке 2.
R6 =R2 \ R1 ={r | r  R2
R2 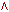 r
r  R1 }
R1 }
| R2 | |||
| Болт М3 | |||
| R5 | |||
| Шифр детали | Название детали | ||
| Гайка М2 | |||
| Болт М1 | |||
| Шайба М1 | |||
| Шайба М3 | |||
| R6 | |
| Шифр детали | Название детали |
| Гайка М4 | |
| Болт М2 |
Следует отметить, что первые две операции, объединение и пересечение, являются коммутативными операциями, то есть результат операции не зависит от порядка аргументов в операции. Операция же разности является принципиально несимметричной операцией, то есть результат операции будет различным для разного порядка аргументов, что и видно из сравнения отношений R5 и R6.
В отличие от навигационных средств манипулирования данными в иерархической и сетевой моделях операции реляционной алгебры позволяют получить сразу иной качественный результат, который является семантически гораздо более ценным и понятным пользователям. Например, сравнение результатов объединения и разности номенклатуры двух участков позволит оценить специфику производства: насколько оно уникально на каждом участке, и, в зависимости от необходимости, принять соответствующее решение по изменению номенклатуры.
Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами.
Кроме трех перечисленных операций в рамках реляционной алгебры определена еще одна теоретико-множественная операция — декартово произведение. Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция декартова произведения, обозначаемая R1  R2, допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.
R2, допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.
Сцеплением, или конкатенацией, кортежей c = <c1, c2, ..., cn> и q = <q1, q2, ..., qm> называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей c и q обозначается как (c , q).
(c, q) = <c1, c2, ... , cn, q1, q2, ..., qm>
Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q.
Все предыдущие операции не меняли степени или арности отношений — это следует из определения эквивалентности схем отношений. Операция декартова произведения меняет степень результирующего отношения.
Декартовым произведением отношения R1 степени n со схемой
SR1 = (A1, A2, ... , An),
и отношения R2 степени m со схемой
SR2 = (B1, B2, ..., Bm),
называется отношение R3 степени n+m со схемой
SR3 = (A1, A2, ... , An, B1, B2, ..., Bm),
содержащее кортежи, полученные сцеплением каждого кортежа r отношения R1 с каждым кортежем q отношения R2.
То есть если R1 = { r }, R2 = { q }
R1  R2 = {(r, q) | r
R2 = {(r, q) | r  R1
R1 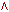 q
q  R2}
R2}
Операцию декартова произведения с учетом возможности перестановки атрибутов в отношении можно считать симметричной. Очень часто операция декартова произведения используется для получения некоторого универсума — т. е. отношения, которое характеризует все возможные комбинации между элементами отдельных множеств. Однако самостоятельного значения результат выполнения операции обычно не имеет, он участвует в дальнейшей обработке.
Группа теоретико-множественных операций избыточна, так, например, операцию пересечения можно заменить сочетанием операций объединения и разности.
(R1  R2) \ (R1 \ R2) \ (R2 \ R1)
R2) \ (R1 \ R2) \ (R2 \ R1)
Однако это достаточно сложная формула, и именно поэтому все три теоретико-множественные операции вошли в базовый набор операций реляционной алгебры.
Далее мы переходим к группе операций, названных специальными операциями реляционной алгебры.
