Инструмент анализа: Корреляция

Лабораторная работа №5

Двумерные данные

Наборы двумерных данных содержат информацию о двух признаках (переменных) для каждого из объектов. В дополнение к изучению обобщающих характеристик каждой из этих двух переменных, рассматриваемых как отдельные наборы одномерных данных, статистические методы анализа двумерных данных используются для изучения связи между этими двумя переменными. При таком анализе необходимо выяснить следующие вопросы.

Ü Существует ли между этими двумя переменными простая связь?

Ü Насколько сильно взаимосвязаны переменные?

Ü Можно ли предсказать значение одной переменной на основании другой? Если да, то с какой степенью надежности?

Ü Существуют ли отдельные объекты или группа объектов, которые требуют особого внимания?

Приведем пример. Цена одной акции (первая переменная) регистрировалась каждый день (вторая переменная) в течение последних шести месяцев. Если установить связь между ценой и временем (датой), то можно увидеть тенденции в изменении стоимости инвестиций. Однако на основании таких данных трудно предсказать будущую стоимость инвестиций. Для этого требуется выяснить, является ли изменение стоимости непредсказуемым (случайным) явлением или существует некоторая реальная закономерность.

При изучении зависимости между двумя переменными рекомендуется в качестве первоначальной цели провести визуальное исследование, а затем вычислить общие характеристики: корреляцию и ковариацию.

Исследование взаимосвязи переменных с помощью диаграмм рассеяния

Для визуального анализа зависимости между двумя переменными используются графики рассеяния. В Excel данный вид графиков называется точечной диаграммой или диаграммой рассеяния. Диаграмма рассеяния позволяет увидеть структуру двумерных данных. Если ваши данные содержат какие-то проблемы (например, выбросы), чаще всего единственный способ их обнаружения состоит как раз в анализе диаграммы рассеяния.

При построении диаграмм рассеяния одна переменная (обозначается буквой Y) рассматривается как зависимая переменная, другая переменная (обозначается буквой X) является независимой переменной, оказывающей влияние на переменную Y. На диаграмме рассеяния переменой X соответствует горизонтальная ось, а переменной Y – вертикальная ось.

Задание 1.

Исследовать визуально зависимость между размером жилой площади и ценой объекта.

В таблице 1 приведены данные, которые представляют 15 объектов недвижимости, проданных в определенном районе города в течение одного календарного года.

Таблица 1. Объекты недвижимости

Объект	Площадь	Цена	Объект	Площадь	Цена
		26,0			37,2
		31,0			38,4
		37,4			43,6
		34,8			44,8
		39,2			40,6
		38,0			41,8
		39,6			45,2
		31,2

В данной задаче естественно ожидать, что цена зависит от жилой площади объекта. Введем обозначения: X – независимая переменная, определяющая размер жилой площади (в квадратных метрах); Y – зависимая переменная, определяющая цену продажи жилого объекта (в тысячах долларов).

1. Откройте программу Excel. Щелкните на кнопке Сохранить на панели инструментов Стандартная. В появившемся диалоговом окне откройте папку Статистика и задайте имя файлу Двумерные данные.xls.

2. На Листе1 расположите данные в столбцах таким образом, чтобы значения X были слева, а значения Y – справа. Для этого в ячейку A1 введите метку Площадь, в ячейку B1 введите метку Цена, а в диапазон A2:B16 введите соответствующие данные из Таблицы 1.

3. Выделите диапазон данных A2:B16 и откройте мастер диаграмм.

4. На шаге 1 выберите тип диаграммы Точечная диаграмма позволяет сравнить пары значений. Щелкните на кнопке Далее>.

5. На шаге 2 на вкладке Диапазон данных убедитесь, что выбран диапазон A2:B16 и включена опция Ряды в: столбцах. На вкладке Ряд проверьте, что ячейки A2:A16 используются как значения для X, а ячейки B2:B16 как значения для Y. Щелкните на кнопке Далее>.

6. На шаге 3 на вкладке Заголовки в текстовом поле Название диаграммы: введите Объекты недвижимости, в текстовом поле Ось X (категорий): введите Жилая площадь, в квадратных метрах, в текстовом поле Ось Y (значений): введите Цена продажи, в тысячах долларов. На вкладке Линии сетки уберите все отметки. На вкладке Легенда снимите флажок Добавить легенду. Щелкните на кнопке Далее>.

7. На шаге 4 убедитесь, что диаграмма будет расположена на имеющемся: листе. Щелкните на кнопке Готово. Расположите диаграмму в диапазоне D1:J16.

8. Для лучшей наглядности отформатируем диаграмму. Измените ось X, чтобы она отображала значения от 400 до 1400. Щелкните правой кнопкой на Оси X (категорий): и в контекстном меню выберите команду Формат оси… На вкладке Шкала в области Авто снимите флажок с опции минимальное значение: и в текстовом поле введите 400, снимите флажок с опции максимальное значение: и в текстовом поле введите 1400, снимите флажок с опции цена основных делений: и в текстовом поле введите 200. Щелкните на кнопке ОК.

9. Измените ось Y, чтобы она отображала значения от 20 до 50 тысяч долларов. Щелкните правой кнопкой на Оси Y (значений): и в контекстном меню выберите команду Формат оси… На вкладке Шкала в области Авто снимите флажок с опции минимальное значение: и в текстовом поле введите 20, снимите флажок с опции максимальное значение: и в текстовом поле введите 50, снимите флажок с опции цена основных делений: и в текстовом поле введите 10. Щелкните на кнопке ОК.

10. Щелкните по названию диаграммы и установите размер шрифта 12. Поочередно щелкните на значениях и заголовках осей (горизонтальной и вертикальной) и установите размер шрифта 10. Дважды щелкните на серой области диаграммы и в диалоговом окне Формат области построения в области Рамка выберите опцию невидимая, а в области Заливка выберите опцию прозрачная. Щелкните на кнопке ОК.

11. Анализ полученной диаграммы показывает определенную зависимость между переменными, а именно: в среднем, чем больше жилая площадь, тем выше отпускная цена.

Инструмент анализа: Корреляция

Корреляция, или коэффициент корреляции является распространенной общей характеристикой двумерных данных в том же смысле, в каком среднее и стандартное отклонение являются важными характеристиками для анализа одномерного набора данных. Коэффициент корреляции характеризует «силу (тесноту)» линейной зависимости между двумя переменными. Возможные значения коэффициента корреляции лежат в диапазоне от –1 до +1. Отрицательный знак коэффициента корреляции указывает на то, что с увеличением значений одной переменной значения другой переменной будут уменьшаться (прямая с отрицательным углом наклона). В случае положительного коэффициента корреляции с увеличением значений одной переменной значения другой переменной также увеличиваются (прямая с положительным углом наклона).

Формула для вычисления выборочного коэффициента корреляции имеет вид:

,

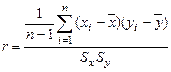где 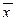и 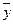– средние значения переменных X и Y, а S_x и S_y – стандартные отклонения этих переменных. Числитель в приведенной формуле включает в себя сумму попарных произведений, которая выражает взаимодействие двух переменных X и Y. Знаменатель в формуле введен для нормирования числителя таким образом, чтобы коэффициент корреляции стал безразмерным, и его можно было легко интерпретировать числом в диапазоне от –1 до +1.

Еще раз подчеркнем, что коэффициент корреляции характеризует только линейную зависимость. Если абсолютная величина коэффициента корреляции равна 1, то это указывает на идеальную (функциональную) линейную взаимосвязь. Если коэффициент корреляции равен 0, то это означает, что между переменными отсутствует линейная зависимость. В таком случае требуется дополнительный анализ, поскольку переменные либо являются независимыми, либо взаимосвязь между ними имеет нелинейный характер.

Задание 2.

Исследовать взаимосвязь между размером жилой площади и ценой объекта.

1. Откройте файл Двумерные данные.xls.

2. С Листа1 скопируйте данные вместе с метками (диапазон A1:B16) на Лист2 в тот же диапазон.

3. На Листе2 в ячейку D1 введите Инструмент анализа: Корреляция.

4. Выберите команду: Сервис®Анализ данных®Корреляция.

5. В диалоговом окне Корреляция установите параметры как указано ниже на рисунке.

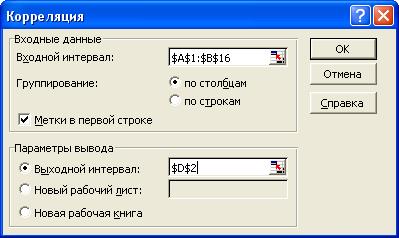
6. Щелкните на кнопке ОК. Результаты будут расположены в диапазоне D2:F4 (см. рисунок ниже).

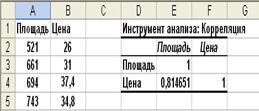
7. Результатом является матрица попарных корреляций. На диагонали расположены 1, показывающие, что каждая переменная положительно коррелированна сама с собой. Значение коэффициента корреляции (0,814651) указано в левой нижней части матрицы в ячейке E4. Правая верхняя часть матрицы пустая, т.к. ее значения совпадают с соответствующими значениями в левой нижней части.

8. Вычислите коэффициент корреляции, используя Мастер функций. Для этого в ячейку D6 введите Функция КОРРЕЛ. Выделите ячейку D7, вызовите Мастер функций и выберите статистическую функцию КОРРЕЛ. В диалоговом окне Аргументы функции щелкните в поле Массив1, а затем выделите диапазон A2:A16, не включая метку. Теперь щелкните в поле Массив2 и выделите диапазон B2:B16, не включая метку. Щелкните на кнопке ОК.

9. Полученное значение коэффициента корреляции (0,814651) близко к 1. Это указывает на то, что между ценой на недвижимость и размером площади существует сильная положительная линейная взаимосвязь. Точки данных довольно плотно сгруппированы (с небольшим случайным отклонением) вокруг прямой, направленной вверх и вправо.

Замечание. В отличие от инструмента анализа Корреляция статистическая функция КОРРЕЛ не статична, т.е. при изменении данных в исходном диапазоне значение коэффициента корреляции, рассчитанного с помощью функции КОРРЕЛ, тоже изменится.

10. Выделите ячейку B2 и введите в нее число 30. Нажмите [Enter].

Обратите внимание!Величина коэффициента корреляции в ячейке D7 изменилась, а в матрице попарных корреляций осталось прежнее значение.

11. Щелкните на кнопке Отменить на панели инструментов Стандартная, чтобы вернуться к исходному значению в ячейке B2.

Попарные корреляции

Инструмент анализа Корреляция особенно полезен при определении попарных корреляций трех и более переменных. Полученные результаты используются для анализа множественной регрессионной модели.

Задание 3.

Исследовать попарные корреляции трех переменных: площадь, оценка, цена.

В таблице 2 данные, которые приведены в таблице 1, дополнены еще одной переменной – оценкой.

Таблица 2. Объекты недвижимости

Объект	Площадь	Оценка	Цена	Объект	Площадь	Оценка	Цена
		7,8	26,0			14,6	37,2
		23,8	31,0			26,0	38,4
		28,0	37,4			30,0	43,6
		26,2	34,8			29,2	44,8
		22,4	39,2			24,2	40,6
		28,2	38,0			29,4	41,8
		25,8	39,6			23,6	45,2
		20,8	31,2

1. Откройте файл Двумерные данные.xls.

2. С Листа1 скопируйте данные вместе с метками (диапазон A1:B16) на Лист3 в тот же диапазон.

3. Выделите столбец B, щелкните на нем правой кнопкой мыши и в контекстном меню выберите команду Добавить ячейки. Данные переменной Цена переместятся в диапазон C1:C16.

4. В ячейке B1 задайте метку Оценка, а в диапазон B2:B16 введите оценки из таблицы 2.

5. В ячейку E1 введите Парные корреляции.

6. Выберите команду: Сервис®Анализ данных®Корреляция.

7. В диалоговом окне Корреляция в поле Входной интервал укажите диапазон данных A1:C16, включая метки. Проверьте, что данные сгруппированы по столбцам и установлен флажок Метки в первой строке.

8. В области Параметры вывода включите опцию Выходной интервал, щелкните в текстовом поле и выделите ячейку E2, определяющую левый верхний угол области вывода результатов. Щелкните на кнопке ОК.

Интерпретация результатов

Выходные данные представляют собой матрицу трех попарных корреляций. Наибольшая корреляция 0,814651 – между Площадью и Ценой. Корреляция между Оценкой и Ценой 0,67537 – меньше и означает меньшую линейную зависимость между этими двумя переменными. Наименьшая корреляция 0,424219 – между Площадью и Оценкой.

Если мы хотим в линейной регрессионной модели использовать для прогноза отпускной цены одну независимую переменную, то полученные парные корреляции показывают, что Площадь больше подходит, чем Оценка, т.к. коэффициент корреляции 0,814651 больше, чем 0,67537.

Если же мы хотим во множественной линейной регрессионной модели использовать для прогноза отпускной цены две независимые переменные, то подойдут Площадь и Оценка, и не будет проблем с их взаимной коррелированностью, т.к. коэффициент корреляции (0,424219) этих двух переменных мал.