Теоретико-множественные модели

Появление теоретико-множественных моделей в системах баз данных было предопределено настоятельной потребностью пользователей в переходе от работы с элементами данных, как это делается в графовых моделях, к работе c некоторыми макрообъектами.

Основной моделью в этом классе является реляционная модель данных. Теоретической основой реляционной модели стала теория отношений, основу которой заложили два логика — американец Чарльз Содерс Пирс (1839-1914) и немец Эрнст Шредер (1841-1902).

Реляционная модель представляет собой совокупность данных, состоящую из набора двумерных таблиц.

В руководствах по теории отношений было показано, что множество отношений замкнуто относительно некоторых специальных операций, то есть образует вместе с этими операциями абстрактную алгебру. Это важнейшее свойство отношений было использовано в реляционной модели для разработки языка манипулирования данными, связанного с исходной алгеброй.

Американский математик Э. Ф. Кодд в 1970 году впервые сформулировал основные понятия и ограничения реляционной модели, ограничив набор операций в ней семью основными и одной дополнительной операцией. Предложения Кодда были настолько эффективны для систем баз данных, что за эту модель он был удостоен престижной премии Тьюринга в области теоретических основ вычислительной техники.

При табличной организации данных отсутствует иерархия элементов. Строки и столбцы могут быть просмотрены в любом порядке, поэтому высока гибкость выбора любого подмножества элементов в строках и столбцах.

Любая таблица в реляционной базе состоит из строк, которые называют записями, и столбцов, которые называют полями. На пересечении строк и столбцов находятся конкретные значения данных. Для каждого поля определяется множество его значений, например, поле «Месяц» может иметь двенадцать значений.

Структура таблицы в реляционной базе характеризуется следующим:

· она состоит из совокупности столбцов;

· каждый столбец имеет уникальное, то есть не повторяющееся в других столбцах, имя;

· последовательность столбцов в таблице не существенна;

· все строки таблицы организованы по одинаковой структуре, то есть имеют одно и то же количество реквизитов и имеют одинаковую длину;

· в таблице нет одинаковых строк;

· количество строк в таблице практически не ограничено;

· последовательность строк в таблице не существенна;

· при выполнении манипуляций с таблицей все строки и столбцы могут просматриваться в произвольном порядке безотносительно к их содержанию и смыслу.

Для этого типа модели имеется развитый математический аппарат – реляционная алгебра. В реляционной алгебре поименованный столбец отношения называется атрибутом, а множество всех возможных значений конкретного атрибута – доменом. Строки таблицы со значениями разных атрибутов называют кортежами.

Например, в таблице, приведенной на рис. 7, кортежи – это d_i1, d_i2,…,d_in (i=1,2,…m); а домены – d_1к, d_2к,…,d_mk (k=1,2,…n). Количество атрибутов, содержащихся в отношении, определяет его степень, а количество кортежей – кардинальность отношения.

	D1	D2	…	Dn
K1	d11	d12	…	d1n
K2	d21	d22	…	d2n
…	…	…	…	…
Km	dm1	dm2	…	dmn

Рис. 22. Домены и кортежи отношения

Один или несколько атрибутов, значения которых однозначно определяют кортеж отношения, называется его ключом, или первичным ключом, или ключевым полем. То есть ключевое поле – это такое поле, значения которого в данной таблице не повторяется. Так, если таблица содержит список сотрудников, и в ней имеются поля: Табельный номер, ФИО, Должность, – то в качестве ключа можно взять поле Табельный номер. Базовые понятия реляционной модели проиллюстрированы на рис. 23.

Рис. 23. Базовые понятия реляционной модели данных

Записи в таблице хранятся упорядоченными по ключу. Ключ может быть простым, состоящим из одного поля, и сложным, состоящим из нескольких полей. Сложный ключ выбирается в тех случаях, когда ни одно поле таблицы однозначно не определяет запись.

Кроме первичного ключа в таблице могут быть вторичные ключи, называемые еще внешними ключами, или индексами.

Индекс – это поле или совокупность полей, чьи значения имеются в нескольких таблицах и которое является первичным ключом в одной из них. Значения индекса могут повторяться в некоторой таблице. Индекс обеспечивает логическую последовательность записей в таблице, а также прямой доступ к записи.

По первичному ключу всегда отыскивается только одна строка, а по вторичному – может отыскиваться группа строк с одинаковыми значениями первичного ключа. Ключи нужны для однозначной идентификации и упорядочения записей таблицы, а индексы для упорядочения и ускорения поиска.

Индексы можно создавать и удалять, оставляя неизменным содержание записей реляционной таблицы. Количество индексов, имена индексов, соответствие индексов полям таблицы определяется при создании схемы таблицы.

Индексы позволяют эффективно реализовать поиск и обработку данных, формирую дополнительные индексные файлы. При корректировке данных автоматически упорядочиваются индексы, изменяется местоположение каждого индекса согласно принятому условию (возрастанию или убыванию значений). Сами же записи реляционной таблицы не перемещаются при удалении или включении новых экземпляров записей, изменении значений их ключевых полей.

С помощью индексов и ключей устанавливаются связи между таблицами. Связь устанавливается путем присвоения значений внешнего ключа одной таблицы значениям первичного ключа другой. Группа связанных таблиц называется схемой данных

СВЯЗИ МЕЖДУ ДАННЫМИ

Данные об объектах в базе связаны между собой. Эти связи принято изображать следующим образом:

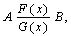
где А и В – объекты;

F(x) – вид связи объекта А с объектом В;

G(x) – вид связи объекта В с объектом А.

Функции F(x) и G(x) могут принимать значения U – единичная и N – множественная связь. Обычно рассматривают четыре вида отношений.

Связь один к одному (1:1):

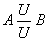
означает, что каждому элементу объекта А может соответствовать только один элемент объекта В и наоборот, например:

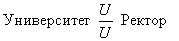
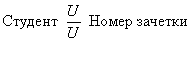
Связь один ко многим (1:N):

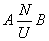означает, что могут существовать экземпляры объекта А, которым соответствует более одного экземпляра объекта В. Но при этом каждому экземпляру объекта В может соответствовать только один экземпляр объекта А, например:

Университет 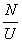Факультеты; Группа 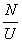Студенты.

Связь многие к одному (N:1)

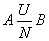означает, что каждому экземпляру объекта А может соответствовать только один экземпляр объекта В, но среди экземпляров объекта В могут быть такие, которым соответствует несколько экземпляров объекта А, например:

Университет 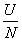Факультеты; Покупатели 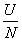Продавец.

Очевидно, что если 1:N – тип связи между А и В, то N:1 – тип связи между В и А.

Связь многие ко многим (N:M), или групповое:

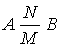
означает, что может существовать экземпляр объекта А, которому соответствует несколько экземпляров объекта В и наоборот. Например:

Преподаватели 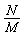Предметы; Покупатели 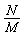Продавцы.