Специальные операции реляционной алгебры
Первой специальной операцией реляционной алгебры является выборка или фильтрация 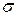 . Для определения этой операции нам необходимо ввести дополнительные обозначения.
. Для определения этой операции нам необходимо ввести дополнительные обозначения.
Пусть с — булевское выражение, составленное из термов сравнения с помощью связок И ( 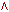 ), ИЛИ (
), ИЛИ ( 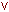 ), НЕ () и, возможно, скобок. В качестве термов сравнения допускаются:
), НЕ () и, возможно, скобок. В качестве термов сравнения допускаются:
- терм А ос а,
где А — имя некоторого атрибута, принимающего значения из домена D; a — константа, взятая из того же домена D, а  D; oc — одна из допустимых для данного домена D операций сравнения;
D; oc — одна из допустимых для данного домена D операций сравнения;
- терм А ос В,
где А, В — имена некоторых θ-сравнимых атрибутов, то есть атрибутов, принимающих значения из одного и то же домена D.
Тогда результатом операции выборки или фильтрации, заданной на отношении R, 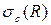 называется отношение R1, включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации с:
называется отношение R1, включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации с:
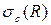 = {r | r
= {r | r  R
R 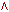 с(r) = "Истина"}
с(r) = "Истина"}
Операция фильтрации является одной из основных при работе с реляционной моделью данных. Условие сможет быть сколь угодно сложным.
Например, выбрать из R10 детали с шифром "0011003". R12 = 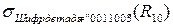
| R12 | ||
| Шифр детали | Название детали | Цех |
| Болт М1 | Цех 1 | |
| Болт М1 | Цех 3 |
Следующей специальной операцией является операция проектирования.
Пусть R — отношение, SR = (A1, ... , An) — схема отношения R.
Обозначим через B подмножество атрибутов отношения R.
Проекцией отношения R на набор атрибутов В, обозначаемой 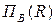 , называется отношение со схемой, соответствующей набору атрибутов В, содержащему кортежи, получаемые из кортежей исходного отношения R путем удаления из них значений, не принадлежащих атрибутам из набора В.
, называется отношение со схемой, соответствующей набору атрибутов В, содержащему кортежи, получаемые из кортежей исходного отношения R путем удаления из них значений, не принадлежащих атрибутам из набора В.
По определению отношений все дублирующие кортежи удаляются из результирующего отношения.
Операция проектирования, называемая иногда также операцией вертикального выбора, позволяет получить только требуемые характеристики моделируемого объекта. Чаще всего операция проектирования употребляется как промежуточный шаг в операциях выборки или фильтрации. Кроме того, она используется самостоятельно на заключительном этапе получения ответа на запрос.
Например, выберем все цеха, которые изготавливают деталь "Болт М1".
Для этого нам необходимо из отношения R10 выбрать детали с заданным названием, а потом полученное отношение спроектировать на столбец "Цех". Результатом выполнения этих операций будет отношение R14:
R13 = 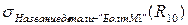 R14 =
R14 = 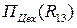
| R13 | |||
| Шифр детали | Название детали | Цех | |
| Болт М1 | Цех 1 | ||
| Болт М1 | Цех 3 | ||
| R14 | |||
| Цех | |||
| Цех 1 | |||
| Цех 3 | |||
Следующей специальной операцией реляционной алгебры является операция соединения.
В отличие от рассмотренных специальных операций реляционной алгебры: фильтрации и проектирования, которые являются унарными, то есть производятся над одним отношением, операция соединения является бинарной, то есть исходными для нее являются два отношения, а результатом — одно.
Операция соединения - производная от операции декартова произведения. Она эквивалентна операции выборки из декартова произведения двух отношений тех кортежей, которые удовлетворяют условию, указанному в предикате соединения.
Типы операций соединения:
· θ – соединение
· соединение по эквивалентности (частный случай θ – соединения)
· естественное соединение
· внешнее соединение
· полусоединение.
θ – соединение определяет отношение, которое содержит кортежи из декартова произведения отношений R и Q, удовлетворяющие предикату β. Предикат имеет вид:
R.ai θ Q.bj. Вместо θ может быть указан один из операторов сравнения (<, <=, >, >=, <>, =).
R 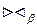 Q =
Q = 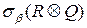
Если предикат β содержит только оператор равенства (=), то соединение называется соединением по эквивалентности.
Пример θ – соединение.
Рассмотрим следующий запрос. Пусть отношение R15 содержит перечень деталей с указанием материалов, из которых эти детали изготавливаются, и оно имеет вид:
| R15 | |||
| Шифр детали | Название детали | Материал | |
| Гайка M1 | сталь-ст1 | ||
| Гайка М2 | сталь-ст2 | ||
| Гайка М3 | сталь-ст1 | ||
| Болт М1 | сталь-ст3 | ||
| Болт М3 | сталь-ст3 | ||
| Шайба М1 | сталь-ст1 | ||
| Шайба М3 | сталь-ст1 | ||
| Гайка М4 | сталь-ст2 | ||
| Болт М2 | сталь-ст3 | ||
| Болт М5 | сталь-ст3 | ||
| Шайба М2 | сталь-ст1 | ||
| R17 | |||
| Название детали | |||
| Гайка M1 | |||
А отношение R16 содержит перечень цехов и шифров изготавливаемых в них деталей.
| R16 Шифр детали | Цех |
| Цех 1 | |
| Цех 3 Цех 1 |
Получим перечень деталей, которые изготавливаются в цеху 1 из материала "сталь-ст1".
R17= 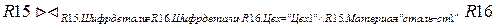 R18=
R18= 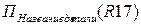
Естественным соединением 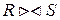 называется соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам X, из результатов которого исключается по одному экземпляру каждого общего атрибута.
называется соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам X, из результатов которого исключается по одному экземпляру каждого общего атрибута.
Естественное соединение – проекция выборки из декартова произведения.
Пример: 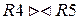
| R4 | |
| Шифр детали | Название детали |
| Гайка M1 | |
| Гайка М3 | |
| Болт М3 |
| R5 Шифр детали | Цех |
| Цех 1 | |
| Цех 3 Цех 1 |
R4 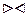 R5 R5 | ||
| Шифр детали | Название детали | Цех |
| Гайка M1 | Цех 1 | |
| Гайка М3 | Цех 3 |
Внешнее соединение
При соединении двух отношений может потребоваться, чтобы строка из одного отношения была представлена в результате соединения, даже если в другом отношении не совпадающего значения. Это достигается с помощью внешнего соединения.
Левым внешним соединением 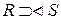 называется соединение, при котором кортежи отношения R, не имеющие совпадающих значений в общих атрибутах отношения S, также включаются в результирующее отношение.
называется соединение, при котором кортежи отношения R, не имеющие совпадающих значений в общих атрибутах отношения S, также включаются в результирующее отношение.
Для обозначения отсутствующих значений во втором отношении используется определитель Null.
Существует также правое внешнее соединение 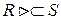 , когда в результирующем отношении содержатся все кортежи правого отношения.
, когда в результирующем отношении содержатся все кортежи правого отношения.
Полусоединение 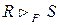
Операция полусоединения определяет отношение, которое содержит те кортежи отношения R, которые входят в соединение отношений R и S.
Операцию полусоединения можно сформулировать с помощью операторов проекции и соединения:
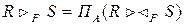
Здесь А – набор всех атрибутов в отношении R. Это полутета-соединение. Существуют полусоединения по эквивалентности и естественное полусоединение.
Последней операцией, включаемой в набор операций реляционной алгебры, является операция деления.
Пусть отношение R определено на множестве атрибутов A, а отношение S – на множестве атрибутов В, причем В 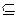 А. Пусть С=А – В, т.е. С является множеством атрибутов отношения R, которые не являются атрибутами отношения S. Тогда результатом деления R ÷ S является набор кортежей отношения R, определенных на множестве атрибутов C, которые соответствуют комбинации всех кортежей отношения S.
А. Пусть С=А – В, т.е. С является множеством атрибутов отношения R, которые не являются атрибутами отношения S. Тогда результатом деления R ÷ S является набор кортежей отношения R, определенных на множестве атрибутов C, которые соответствуют комбинации всех кортежей отношения S.
Операция деления может быть заменена последовательностью других операций:
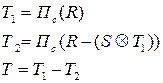
Пример.
Пусть делимое – отношение D1, содержащее номера поставщиков (SN) и номера поставляемых ими деталей (PN). Делители – отношения DOR, представленные ниже:
| SN | PN |
| S1 | P1 |
| S1 | P2 |
| S1 | P3 |
| S1 | P4 |
| S1 | P5 |
| S1 | P6 |
| S2 | P1 |
| S2 | P2 |
| S3 | P2 |
| S4 | P2 |
| S4 | P4 |
| S4 | P5 |
D1
DOR DOR DOR
| PN |
| P1 |
| P4 |
| PN |
| P1 |
| PN |
| P1 |
| P2 |
| P3 |
| P4 |
| P5 |
| P6 |
Результат деления D1 ÷ DOR:
| SN |
| S1 |
| S4 |
| SN |
| S1 |
| SN |
| S1 |
| S2 |
В последнем случае делителем является отношение, содержащее номера поставщиков, поставляющих все детали. Операция деления полезна именно для запросов такого рода. Если запрос на обычном языке включает слово «все» или «каждый» («получить поставщиков, поставляющих все детали»), то нужна операция деления.
Реляционное исчисление
| Введение Реляционное исчисление – альтернативный реляционной алгебре подход к определению реляционных операторов. В отличие от алгебры, которая предоставляет набор операций, позволяющий из данных отношений построить нужное отношение, исчисление представляет систему обозначений для определения необходимого отношения в терминах данных отношений. В исчислении просто описывается требуемый результат, а в алгебре указывается процедура получения результата. Алгебра и исчисление эквивалентны в том смысле, что каждому выражению в исчислении соответствует эквивалентное выражение в алгебре и наоборот, т.е. между ними существует взаимно-однозначное соответствие. Реляционное исчисление является прикладной ветвью формального механизма исчисления предикатов первого порядка. В основе исчисления лежит понятие переменной с определенной для нее областью допустимых значений и понятие правильно построенной формулы, опирающейся на переменные, предикаты и кванторы. В зависимости от того, что является областью определения переменной, различают исчисление кортежей и исчисление доменов. В исчислении кортежей областями определения переменных являются тела отношений базы данных, т. е. допустимым значением каждой переменной является кортеж тела некоторого отношения. В исчислении доменов областями определения переменных являются домены, на которых определены атрибуты отношений базы данных, т. е. допустимым значением каждой переменной является значение некоторого домена. Мы рассмотрим более подробно исчисление кортежей. Используем синтаксис, близкий с синтаксисом языка баз данных QUEL, который долгое время являлся основным языком известной реляционной СУБД Ingres. |
Исчисление кортежей
Для определения кортежной переменной используется оператор RANGE. Например, для того чтобы определить переменную СЛУЖАЩИЙ, областью определения которой является отношение СЛУЖАЩИЕ, нужно употребить конструкцию
RANGE OF СЛУЖАЩИЙ IS СЛУЖАЩИЕ;
Как уже говорилось, из этого определения следует, что в любой момент времени переменная СЛУЖАЩИЙ представляет некоторый кортеж отношения СЛУЖАЩИЕ. При использовании кортежных переменных в формулах можно ссылаться на значение атрибута переменной. Например, для того, чтобы сослаться на значение атрибута СЛУ_ИМЯ переменной СЛУЖАЩИЙ, нужно употребить конструкцию СЛУЖАЩИЙ.СЛУ_ИМЯ.
