Определение статических параметров
Экспериментальные исследования лабораторной работы
Определение статических параметров
Проводимые измерения:
1. Измерение входных токов операционного усилителя (ОУ).
2. Оценка величин среднего входного тока и разности входных токов активного фильтра (АФ).
3. Измерение частоты среза АФ,
4. Измерение амплитудно-частотную характеристику АФ.
5. Вычисление выходного сопротивления ОУ.
Исследования будем проводить на следующих фильтрах с различной полосой пропускания:
1. Фильтрах нижних частот (ФНЧ) — пропуская сигнал, который ниже определенной частоты (ее еще именуют частотой среза).
2. Фильтрах высоких частот (ФВЧ) — пропуская сигнал выше частоты среза.
3. Полосовых фильтрах — пропуская только определенный диапазон частот.
4. Режекторных фильтра — задерживаая только определенный диапазон частот
Используемые приборы и элементы
Вольтметр, амперметр, осциллограф, источник напряжения, ОУ ТL071, резисторы, конденсаторы.
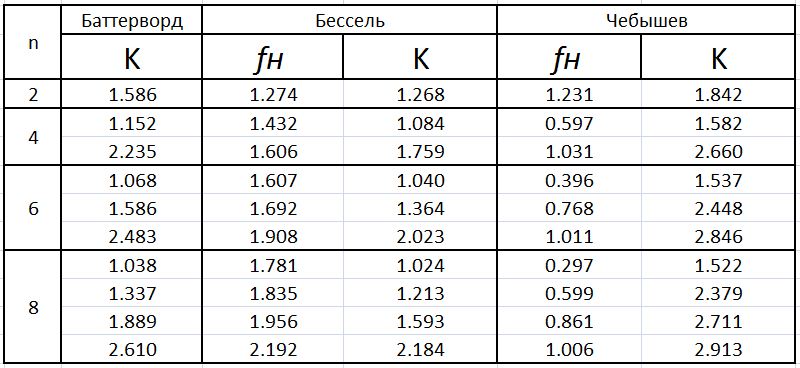
А самый простой — это «табличный» метод показаны в таблице.
Т а б л и ц а 1 – расчет АФ для ФНЧ
Задание 1. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда.
Имея фильтр n-ного четного порядка, это означает, что в нем будет n/2 ОУ. В данном задании — один указанном на рисунке 1.
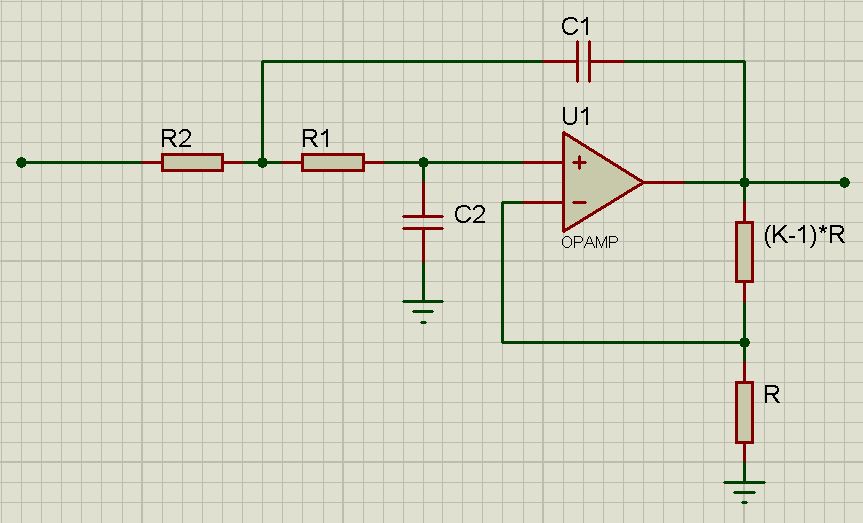
Рисунок 1 – Схема активного ФНЧ
Для данного типа расчета берется во внимание, что R1 = R2, C1 = C2.
Смотрим в табличку. Видим, что К = 1.586. Это нам пригодится чуть позже.
Для фильтра низких частот справедливо:
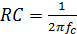 ,
,
где fc – частота среза.
Сделав подсчет, получаем RC=0.0011. Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора. Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение R берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления R = 10 кОм, а верхний 5.8 кОм.
Задание 2ю Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя.
Раз фильтр четвертого порядка, то в схеме будет два ОУ показанной на рисунке 2. Тут все совсем не сложно. Каскадно включаем 2 схемы ФВЧ.
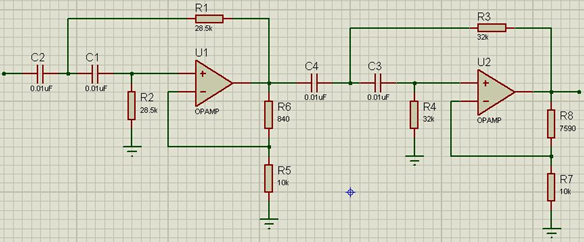
Рисунок 2 – Схема активного ФВЧ четвертого порядка
Как видим, для фильтра четвертого порядка у нас аж 2 значения К. Логично, что первое предназначается для первого каскада, второе — для второго. Значения К равны 1.432 и 1.606 соответсвенно. Таблица была для фильтров низких частот. Для расчета ФВЧ надо кое-что изменить. Коэффициенты К остаются такими же в любом случае. Для характеристик Бесселя и Чебышева изменяется параметр fH - нормирующая частота. Она будет равна 1/ fH.
Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула
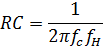
Учтите, что для каждого отдельного каскада придется считать отдельно.
Для первого каскада
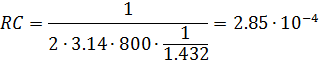
Пусть С = 0.01 мкФ, тогда R = 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом.
Для второго каскада
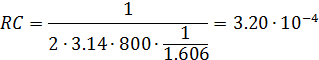
Емкость конденсатора оставим неизменной. Раз С = 0.01 мкФ, то R = 32 кОм.
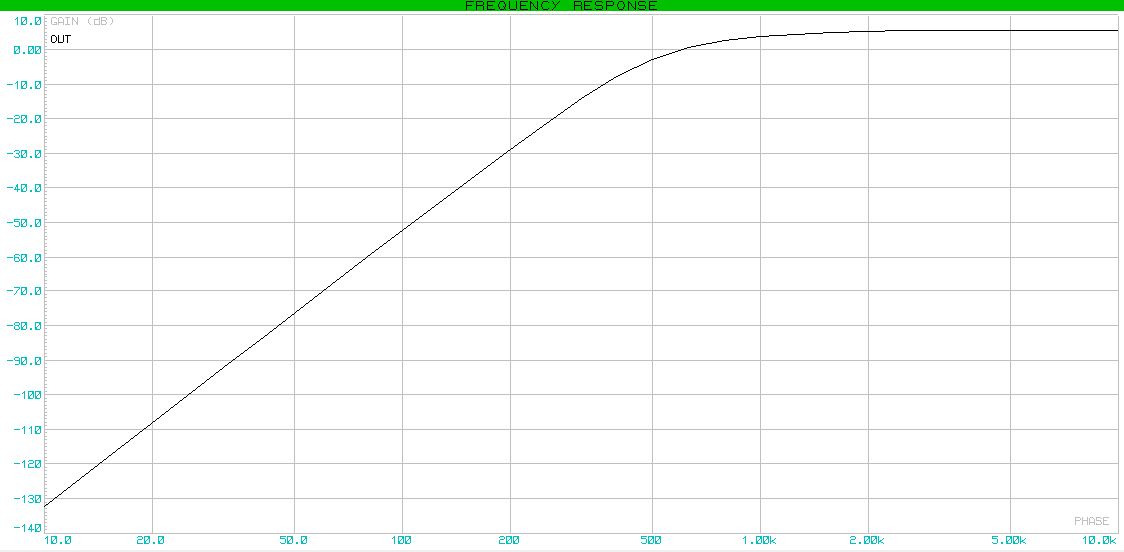
Рисунок 2 – АЧХ активного ФВЧ четвертого порядка
Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик.
Для полосовых и режекторных фильтров также можно использовать «табличный метод», но тут немного другие характеристики.
Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка.
Т а б л и ц а 1 – расчет АФ для полосового фильтра четвертого порядка

a1 и b1 — расчетные коэффициенты. Q — добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад. Δf — диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент α — еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете.
Задание # 3. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1.
Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчетными элементами.
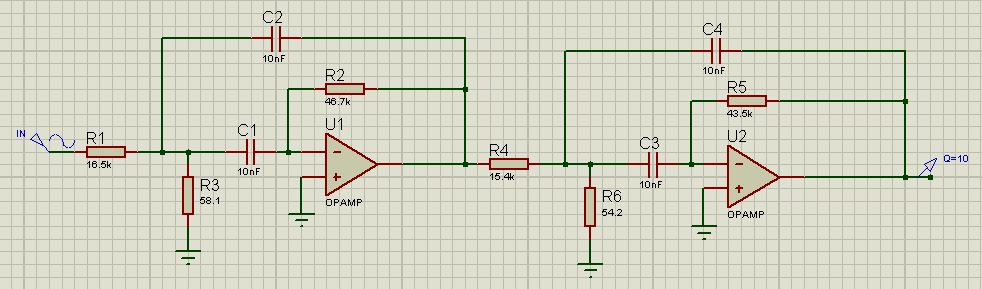
Рисунок 3 – Полосовой фильтр четвертого прядка
Для первого фильтра центральная частота определяется как
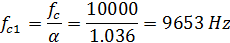
Для второго фильтра
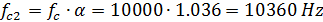
Конкретно в нашем случае, опять же из таблицы, определяем, что добротность Q = 10. Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна
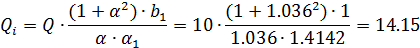
Поправка усиления для области центральной частоты:
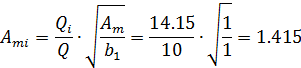
Финальная стадия — расчет компонентов.
Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра
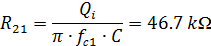
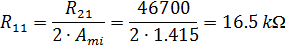
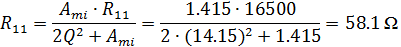
В том же порядке, что и (1) находим R22 = R5 = 43.5 кОм, R12 = R4 = 15.4 кОм, R32 = R6 = 54.2 Ом. Только учтите, что для второго фильтра используем fc2..
Ну и на последок, АЧХ.
Следующая остановка — полосно-заграждающие фильтры или режекторные.
Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка.
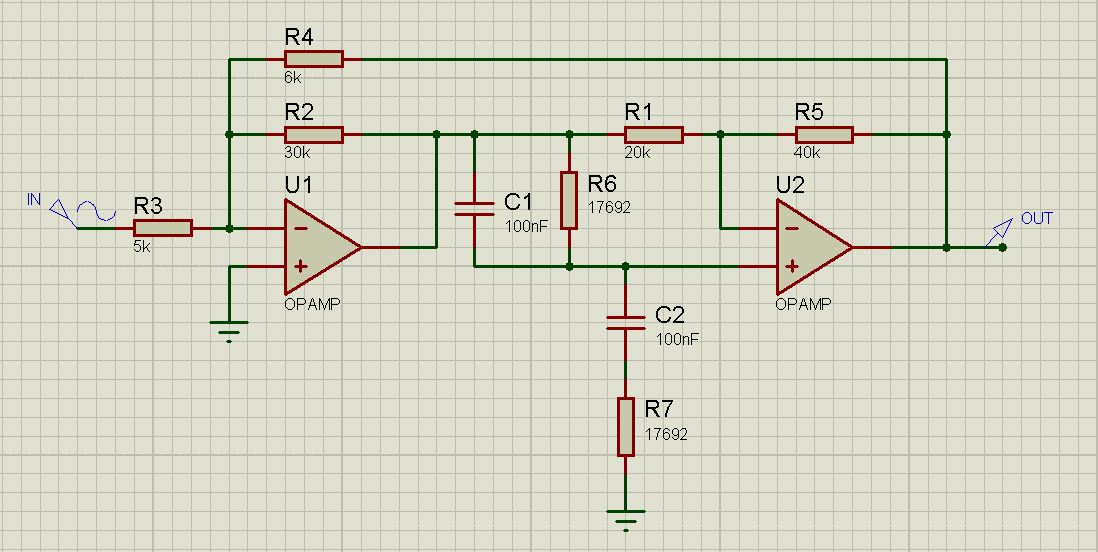
Наше последнее задание.
Задание # 4. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью Q = 2 и коэффициентом усиления в полосе пропускания равным 1.
Прежде всего, произвольно выбираем емкость конденсатора. Допустим, С = 100 нФ.
Определим значение R6 = R7 = R
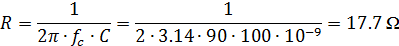
Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра.
Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность.
α=3Q-1=6-1=5
β=-A0  3Q=-6
3Q=-6
Выберем произвольно резистор R2. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм.
Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания.
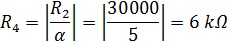
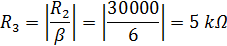
И на последок, необходимо произвольно выбрать R5 = 2R1. У меня в схеме эти резисторы имеют значение 40 кОм и 20 кОм соответственно.
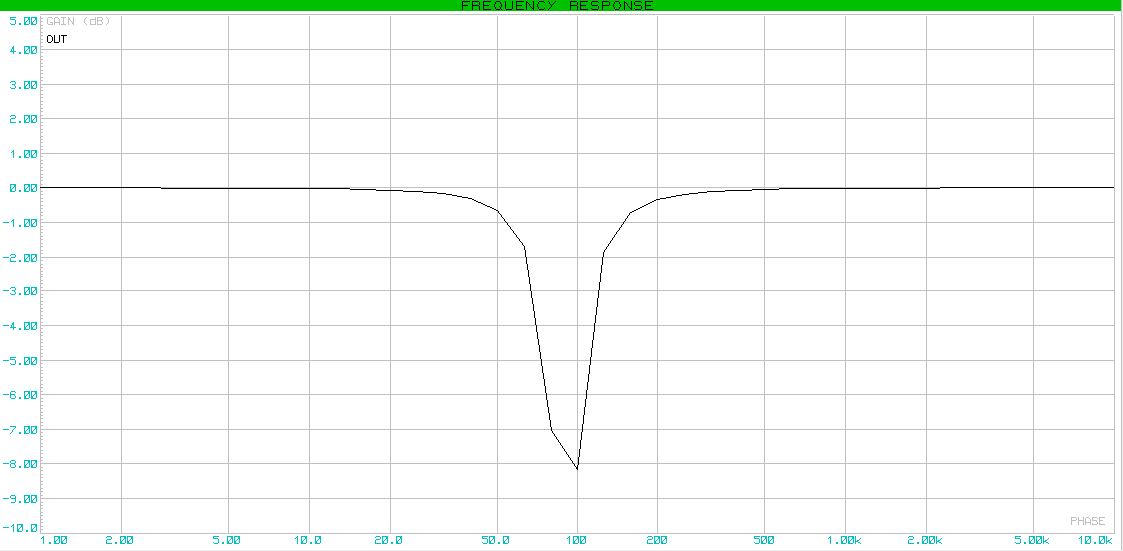
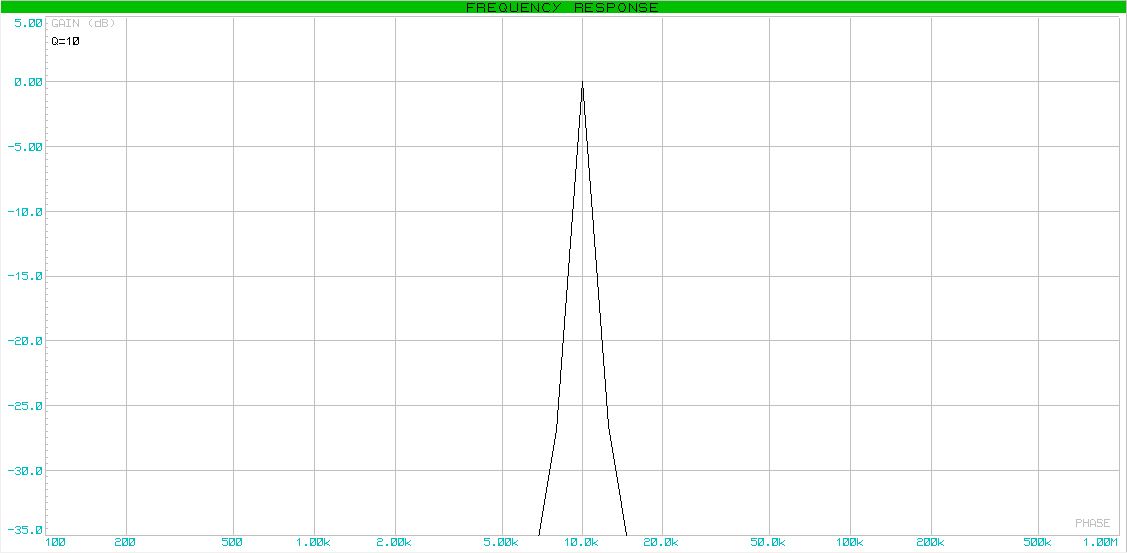
Собственно, АЧХ: