Центральные проблемы многомерного стат. анализа и моделирования
Проблема 1. Статистическое исследование структуры и характера взаимосвязей, существующих между анализируемыми количественными переменными. Методам и моделям, предназначенным для решения различных постановок задач в рамках данной модели, посвящена эконометрика.
Проблема 2. Разработка статистических методов классификации объектов и признаков. В общей (нестрогой) постановке проблема классификации объектов заключается в том, чтобы всю анализируемую совокупность объектов 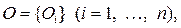 статистически представленную в виде матрицы (2.1’ /см 12 вопрос/) или
статистически представленную в виде матрицы (2.1’ /см 12 вопрос/) или 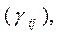 разбить на незначительно большое число (заранее известное или нет) однородных, в определенном смысле, групп или классов. Для формализации этой проблемы удобно интерпретировать анализируемые объекты в качестве точек в соответствующем признаковом пространстве. Если исходные данные представлены в форме матрицы (2.1’), то эти точки являются непосредственным геометрическим изображением многомерных наблюдений
разбить на незначительно большое число (заранее известное или нет) однородных, в определенном смысле, групп или классов. Для формализации этой проблемы удобно интерпретировать анализируемые объекты в качестве точек в соответствующем признаковом пространстве. Если исходные данные представлены в форме матрицы (2.1’), то эти точки являются непосредственным геометрическим изображением многомерных наблюдений
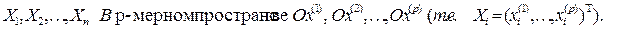 Если исходные данные представлены в форме матрицы
Если исходные данные представлены в форме матрицы 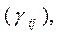 то исследователю неизвестны непосредственно координаты этих точек, но зато задана структура парных расстояний (близостей) между объектами. Естественно предположить, что геометрическая близость двух или нескольких точек в этом пространстве означает близость «физических» состояний, соответствующих объектов, их однородность. Тогда проблема классификации состоит в разбиении анализируемой совокупности точек-наблюдений на сравнительно небольшое число (заранее известное или нет) классов таким образом, чтобы объекты находились бы на сравнительно небольших расстояниях друг от друга. Полученные в результате разбиения классы часто называют кластерами (таксонами, образами).
то исследователю неизвестны непосредственно координаты этих точек, но зато задана структура парных расстояний (близостей) между объектами. Естественно предположить, что геометрическая близость двух или нескольких точек в этом пространстве означает близость «физических» состояний, соответствующих объектов, их однородность. Тогда проблема классификации состоит в разбиении анализируемой совокупности точек-наблюдений на сравнительно небольшое число (заранее известное или нет) классов таким образом, чтобы объекты находились бы на сравнительно небольших расстояниях друг от друга. Полученные в результате разбиения классы часто называют кластерами (таксонами, образами).
В зависимости от наличия и характера априорных сведений о природе искомых классов и от конечных прикладных целей исследования приходится обращаться к ряду методам. Дискриминантный анализ, процедуры кластер-анализа, многомерное шкалирование и др.
Проблема 3. Снижение размерности исследуемого признакового пространства для более доступного объяснение природы анализируемых многомерных данных. Априорное допущение состоит в том, что существует небольшое число (в сравнении с числом р исходных анализируемых данных 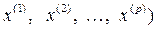 , число
, число 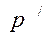 признаков-детерминант (главные компоненты, общие факторы, наиболее информативные объясняющие переменные), с помощью которых могут быть достаточно точно описаны анализиуемые переменные наблюдаемых объектов, при этом главные факторы могут находиться среди исходных признаков, а могут быть латентными, т.е. непосредственно статистически не наблюдаемыми, но восстанавливаемыми по исходным данным вида (2.1), (2.1’), (2.2) /все эти м-цы см. в 12 вопросе/
признаков-детерминант (главные компоненты, общие факторы, наиболее информативные объясняющие переменные), с помощью которых могут быть достаточно точно описаны анализиуемые переменные наблюдаемых объектов, при этом главные факторы могут находиться среди исходных признаков, а могут быть латентными, т.е. непосредственно статистически не наблюдаемыми, но восстанавливаемыми по исходным данным вида (2.1), (2.1’), (2.2) /все эти м-цы см. в 12 вопросе/
Необходимость снижения исходного признакового пространства с целью лаконичного (более доступного) объяснения природы анализируемых многомерных данных может быть продиктована различными прикладными задачами статистического анализа и моделирования.
1. отбор наиболее информативных показателей (включая выявление латентных факторов). Имеется в виду решение задачи об отборе из исходного (априорного) множества признаков 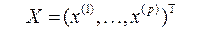 или о построении в качестве некоторых комбинаций исходных признаков относительно небольшого числа
или о построении в качестве некоторых комбинаций исходных признаков относительно небольшого числа 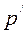
переменных 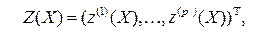 которые обладали бы свойством наибольшей информативности в смысле, определенном, как правило, некотороым специальным подобранным для задач критерием информативности
которые обладали бы свойством наибольшей информативности в смысле, определенном, как правило, некотороым специальным подобранным для задач критерием информативности 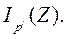
2. сжатие массивов обрабатываемой и хранимой информации. Этот тип задач тесно связан с предыдущим и в частности требует в качестве одного из основных приемов решения построения экономной системы вспомогательных признков, обладающих автоинформированностью, т.е. свойством автопрогноза. В свою очередь методы классификации зачастую позволяют перейти от массива, содержащего информацию по всем n статистически обследованным объектам к соответствующей информации только по k эталонным образцам (k<<n). Методы снижения размерности позволяют заменить исходную системы показателей 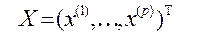 набором вспомогательных переменных
набором вспомогательных переменных 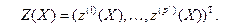 Таким образом, размерность информационного массива понижается от p*n до
Таким образом, размерность информационного массива понижается от p*n до 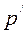 *k, т.е. во многие десятки раз , если учесть что p и n на порядок выше соответсвенно чем
*k, т.е. во многие десятки раз , если учесть что p и n на порядок выше соответсвенно чем 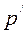 и k.
и k.
3. визуализация (наглядное представление данных). При формировании рабочих гипотез, исходных допущений о геометрической и вероятностной природе совокупности анализируемых данных 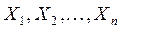 важно было бы «подсмотреть», как эти данные-точки располагаются в анализируемом пространстве. Речь идет о геометрической иллюстрации математических соотношений в трехмерном пространстве и их проецировании на плоскости. Причем здесь попутно может возникнуть задача снижения анализируемой совокупностив соответствии с некоторым специально сформулированным критерием и оговоренным условием о том, что размерность редуцированного пространства не должна превышать трех. Аппарат решения подобных задач присутствует в рамках методов главных компонент и факторного анализа.
важно было бы «подсмотреть», как эти данные-точки располагаются в анализируемом пространстве. Речь идет о геометрической иллюстрации математических соотношений в трехмерном пространстве и их проецировании на плоскости. Причем здесь попутно может возникнуть задача снижения анализируемой совокупностив соответствии с некоторым специально сформулированным критерием и оговоренным условием о том, что размерность редуцированного пространства не должна превышать трех. Аппарат решения подобных задач присутствует в рамках методов главных компонент и факторного анализа.
4. Построение условных координантных осей (многомерное шкалирвоание, латентно-структурный анализ).
