Базы знаний. Модели представления знаний
В качестве ядра интеллектуальных систем рассматривают базу знаний, создаваемой на основе методов инженерии знаний, научного направления предназначенного для изучения моделей и методов извлечения и формализации (представления) знаний эксперта (человека), необходимых для использования в практике управления. Состав данного направления представлен на рис. 5.6.
Рис. 5.6. Составляющие инженерии знаний
Базу знаний, как способ представления знаний в памяти компьютера, следует рассматривать отдельно из-за ее исключительной перспективности в формировании решений. Будучи предметом изучения специального научного направления, известного под названием инженерия знаний, базы знаний легли в основу создания экспертных систем, одного из продуктов искусственного интеллекта. Далее под базой знаний будем понимать структурированные знания, то есть знания человека (эксперта, специалиста), помещенные в память компьютера в соответствии с некоторой моделью.
Модель, как известно, - это правила или соглашения, выполнение которых позволяет представить нечто в памяти компьютера в том виде, которая позволяет использовать формальные (программные) средства для их обработки (получение новых знаний).
Существуют различные модели представления знаний, среди которых наиболее популярными являются:
- онтологии;
- семантические (ассоциативные) сети;
- продукционные модели (деревья вывода);
- деревья целей;
- нечеткие множества;
- нейросети.
Рассмотрим последние три и поясняющие их примеры.
Дерево целей является дальнейшим совершенствованием целевого управления, известного сегодня как Goal-управление. В основу его построения положено понятие цели, измерение достижения которой осуществляется с помощью значений соответствующих экономических показателей.
Пример.
Разработка дерева целей для повышения рентабельности собственного капитала и определение расчетных формул для прямых вычислений
Рис. . Фрагмент дерева расчета показателей
В простейших случаях, при наличии аддитивной функции и при положительном знаке желаемого прироста функции, а также приростов аргументов, задача решается просто. Для определения неизвестных приростов аргументов достаточно задаваемый прирост функции распределить пропорционально коэффициентам приоритетности целей. Допустим, известна следующая целевая установка, заданная аддитивной функцией вида α, β — коэффициенты приоритетности целей. Известен также задаваемый прирост функции, равный , который следует получить в результате увеличения обоих аргументов.
Для решения задачи можно записать следующее: откуда получим
Пример 1.Пусть В = 20, С = 12, А = 32, ΔА = 8,
Представим графически дерево:
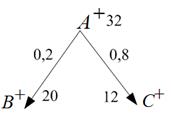
Тогда
Проверим результат: 20+1,6+12+6,4=40.
Пусть дерево целей, согласно которому происходят расчеты, представлено на рис. 4.1. Показатели в узлах дерева снабжены указателями подцелей («плюс» — увеличение, «минус» — снижение), отражающими направления их изменения, а греческими буквами представлены коэффициенты приоритетности в достижении подцелей. Пунктирными стрелками указаны качественные показатели, приросты для которых не рассчитываются, а задаются пользователем. Такие показатели, используемые в качестве констант, обозначены словом const.
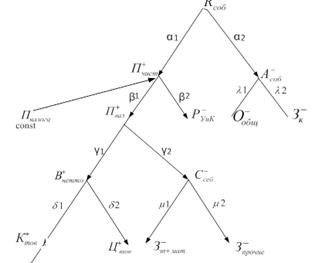
Рис. 4.1. Дерево целей «Повышение уровня рентабельности собственного капитала»
Рассмотрим несколько уровней дерева. Для решения задачи можно воспользоваться следующими расчетными формулами:
где — рентабельность собственного капитала; — чистая прибыль; — величина собственного капитала;
где — общая стоимость активов; — величина заемного капитала;
где — валовая прибыль; — процент налога на прибыль; — управленческие и коммерческие расходы;
где — выручка (нетто); — себестоимость продукции;
где — количество реализованных товаров; — продажная цена товаров;
где — затраты на материалы и заработную плату; — прочие затраты;
Рассчитаем фактическое значение рентабельности. Для этого создадим в среде MS Excel таблицу (см. рис. 4.2), вычисления в которой осуществляются сверху-вниз (конечный показатель расчетов находится внизу таблицы). Для этого необходимо следующее.
