Максимальное среднее количество информации переносимое двоичным сигналом

Турбо код

Число перестановок

Энтропия

Распределение Лапласа

Лемма Каца

2.Свойства энтропии: когда элементы ансамбля Х равновероятны

H(x) 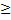Максимальное среднее количество информации переносимое двоичным сигналом - student2.ru log|X|

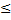H(X) Максимальное среднее количество информации переносимое двоичным сигналом - student2.ru H(Y)

H(X)≤log|X|

H(X)≠H(X)

H(X) = log |X|

3. Свойство энтропии : если для двух ансамбля X и Y распределения вероятностей представляет собой одинаковые набор чисел

H (X) = H (Y)

H (X) < H (Y)

H (X)≥ H (Y)

H (X) ≠ H (Y)

H (X) -H (Y)=0

4.Квантования по уровню-

Процесс обработки конечных по значениям аналоговых сигналов в конечное число цифровых значений

Процесс преобразования из бесконечного числа значений аналоговых сигналов в конечное число цифровых значений

Процесс преобразования конечных значений аналоговых сигналов в бесконечное число цифровых значений

Процесс передачи бесконечных по значениям аналоговых сигналов в конечное число цифровых значений

Процесс модуляции бесконечных значений аналоговых сигналов в бесконечное число цифровых значеньтиний

5.Состав дискретного канала

Прерывный канал модулятор демодулятор

Дискретный канал модулятор демодулятор

Непрерывный канал модулятор демодулятор

Полунепрерывный канал модулятор демодулятор

Непрерывный канал кодер демодулятор

6.угловая модуляция

Импульсная и фазовая модуляция

Амплитудная и фазовая модуляция

Частотная и фазовая модуляция

Частотная и гармоническая модуляция

Частотная и дискретная модуляция

7. Результат выполнения операции дискретизации

Переход от непрерывной формы представления сигнала к дискретной

Переход от плунепрерывной формы представления сигнала с дискретной

Переход от дискретной формы представления сигнала к непрерывной

Переход от прерывной формы представления сигнала к дискретной

Переход от непрерывного по частотам канала

8. Канал с аддитивным белым гауссовским шумом (АБГШ)

Модель прерывного во времени канала

Модель непрерывного по времени канала

Модель полунепрерывного по времени канала без памяти

Модель непрерывного по частотам канала

Модель дискретного по времени канала

9. Применения помехоустойчивого кодирования

Обнаружение и исправление ошибок возникающих при передачи по дискретному каналу

10. связи с отдельными частями сообщения отражаются

Синтаксическими отношениями

11. в структурном подходе к измерению информации различаются мера информации

Геометрическая комбинаторная и аддитивная

12. среднее количество информации содержащийся в принятом ансамбле сообщения в относительно переданного ансамбля сообщений а в условиях помех определяется с условиями

Энтропия объединения и условной энтропии

13. для удобства исчисления энтропии сообщений передаваемых двоичным кодом Шеннона заменил используемый термодинамикой двоичным log2

Натуральный лагорифм

14. Одна из теорем из Шеннона свидетельствует об информационной энтропии множества

Уменьшении

15. ответ. Дискретная функция

Дискретная функция непрерывного аргумента

16. назначение декодера канала-

Восстановление с помощью корректирующих бит информационной последовательности

17. Гауссов канал

Многомерный и шум имеет гауссово распределение

18. Белый шум