Информация. информационные процессы. источники и потребители информации. форма представления информации. вероятностный подход к измерению информации. формулы хартли и шеннона

Информация.Известно, что история развития человечества условно делится на три этапа. На первом происходило «покорение» вещества: обработка материалов и изготовление различных предметов, добыча руды и плавка металлов и так далее. Этот этап закончился приблизительно во второй половине XVIII века, после изобретения Ползуновым (1763 г.) и Уаттом (1784 г.) паровой машины. Наступившая эра по праву может быть названа эрой энергии. Около двухсот лет человек искал новые и новые источники энергии и разрабатывал системы для её получения, переработки, передачи, хранения и использования. И, наконец, в середине XX века началась эра информации, продолжающаяся до сих пор. Таким образом, наблюдается своеобразный эволюционный ряд: вещество → энергия → информация. Неправильно было бы считать, что с наступлением новой эры старая уходит в прошлое. Вернее говорить о смене акцентов.

Определение информации. Информационные процессы Информация (от лат. informatio) — разъяснение, изложение. Информация передаётся как сообщение в виде сигнала от источника к приёмнику по каналу связи. Примеры: речь, музыка, TV. Сообщение передаётся через какую-либо материальную среду. В канале связи всегда существуют помехи (шум), искажающие сигнал. Такой процесс передачи информации называется информационным процессом. Сигнал представляет собой любой процесс переноса информации. Сообщение — это информация, представленная в определённой форме и предназначенная для передачи. Данные — это информация, представленная в формализованном виде и предназначенная для обработки её техническими средствами, например, ЭВМ. Восприятие информации — субъективно. Пример: Джордан забивает трёхочковый мяч за две секунды до конца матча. Это высказывание понятно тем, кто интересуется баскетболом и следит за играми NBA и вряд ли будет понято остальными. 1.2 Формы представления Формы представления информации: непрерывная и дискретная. Сигнал называется непрерывным, если его параметр в заданных пределах может принимать любые промежуточные значения. Сигнал называется дискретным, если его параметр в заданных пределах может принимать отдельные фиксированные значения. Вероятностный подход Количеством информации называют числовую характеристику сигнала, отражающую ту степень неопределённости (неполноту знаний), которая исчезает после получения сообщения в виде данного сигнала. Эту меру неопределённости называют энтропией. I=H1-H2. Если в результате получения сообщения достигается полная ясность в каком-то вопросе (H2=0), то говорят, что была получена полная информация. Наоборот, если после получения сообщения неопределённость осталась прежней (H1=H2, I=0), то информации получено не было. Очевидно, между понятиями информация, неопределённость и возможность выбора имеется связь. Так, неопределённость предполагает возможность выбора (угадайте карту), а информация, уменьшающая неопределенность, уменьшает и возможность выбора (угадайте красную карту). При полной информации выбора нет (угадайте даму пик).

Равновероятные состояния. Рассмотрим вначале случай, когда состояния возникают с равной вероятностью. Например, бросание монеты или игральной кости. В первом случае возможно два исхода опыта, а во втором — шесть. Сколько же информации мы получим после одного опыта? Тот же вопрос можно поставить и по-другому: какова неопределённость в состоянии системы (допустим, кубик или монета уже подброшены)? Связь между количеством информации и числом равновозможных состояний системы задаётся формулой Хартли: I =H=log₂N, где N — число равновозможных состояний.

Единицы измерения информации. При N=2 получим I= log2 2= 1. Т. е. единица информации получается при проведении опыта над системой с двумя равновероятными состояниями. Единица информации называется бит (англ. BInary digiT). 8 бит составляют байт. Другие кратные величины образуются следующим образом: 210 =1024 байта— килобайт (КБ), 1024 КБ — мегабайт (МБ), 1024 МБ — гигабайт (ГБ), 1024 ГБ — терабайт (ТБ), 1024 ТБ — петабайт (ПБ), 1024 ПБ — экзабайт (ЭБ) и т. д.

Неравновероятные состояния В том случае, когда состояния системы неравновероятны (шулерская монета), получится другое выражение для количества информации. Рассмотрим систему с N неравновероятными возможными состояниями. Пусть над этой системой произвели m опытов, причём состояние с номером i реализовалось n(i) раз. Очевидно, что 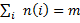. Тогда вероятность выпадения i-го состояния равна pi=ni/m и среднее количество неопределённости, которое снимается одним опытом, вычисляется по известной формуле Шеннона: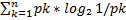

Например, H может быть количеством информации, приходящимся (в среднем) на один символ полученного сообщения. Пример 1. Вычислить информацию, содержащуюся в сообщении: ААБАГВББВА. Здесь 4 N (количество различных букв в сообщении), 10 m (общее количество символов в сообщении). Вычислим количество каждой буквы в сообщении и соответствующую вероятность: Буква (i) А Б В Г Кол-во ( i n ) 4 3 2 1 Pi 4/10 3/10 2/10 1/10 Подставим в формулу: H = - (0.4* log2 0.4 + 0.3* log2 0.3 +0.2* log2 0.2 +0.1* log2 0.1) = 1.8464 бит. Такое количество информации несёт в среднем каждая буква в этом сообщении. Чтобы вычислить общую информацию, содержащуюся в сообщении, надо эту среднюю величину умножить на количество символов в сообщении, то есть на m . Получим: 464.188464.110  HmH общ (бита