Решение задач нелинейной оптимизации на примере Модели агентских отношений

Решение проблемы морального риска: участие в прибылях

Основные понятия и методы теории контрактов рассматриваются подробно в отдельных учебных курсах[1]. Отдельные понятия описаны в приложении. Один из разделов теории контрактов - Теория агентства

Одной из задач этой теории является поиск и анализ оптимальных стимулирующих схем вознаграждения.

Контракт (лат. contractus, от лат. contrahere – соединять вместе). Взаимное соглашение двух или нескольких лиц, по которому одно из них или несколько обязуются что-либо сделать. Будем рассматривать понятие контракт в более узком смысле. Будем считать , что это письменное условие о найме на работу в котором оговорены права и обязанности для его участников. Как правило, в обязанности работника входит выполнение некоторой работы, а в обязанности работодателя – создание условий для её выполнения и выплата оговоренного вознаграждения.

В теории контрактов одну из сторон называют агентом, а другую – принципалом. Их главные отличия – различное отношение к своим обязательствам и к риску, а также в уровне информированности.

· Принципал выполняет взятые на себя обязательства по выплате вознаграждения агенту.

· Агент может относиться к своим обязательствам оппортунистически (см. приложение).

· Принципал более склонен к риску, чем агент. Это проявляется в различном виде функция полезности ( см.курсы микро и макроэкономики, а также приложение 2), которые определяют целесообразность поведения сторон

· Существует асимметрия в информированности. Агент обладает некоторой (важной для выполнения контракта) информацией, а принципал – нет.

Будем рассматривать простейшую модель.

В рамках рассматриваемой модели работник будет агентом, а работодатель –принципалом, Объем выполняемой работы и, главное, её качество определяется уровнем усилий, который прилагает агент для её выполнения. (Объем выполняемой работы будем считать фиксированным и не вызы ающим разногласий между сторонами.)

В модели рассматриваются два индивида – поручитель (принципал, патрон) и исполнитель (агент). Агент может выполнять свои договорные обязательства с разным уровнем усилий, например, работать интенсивно или отлынивать. Важно то, что он сам выбирает уровень усилий, а принципал не может объективно проверить (верифицировать) какой уровень усилий прикладывался.

Контракты, формируемые в рамках рассматриваемой модели, должны быть направлены на обеспечение добровольных неверифицируемых действий, которые приносили бы выгоду обеим сторонам.

Обозначим через 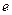уровень усилий агента. Конечный результат для приципала в значительной степени определяется значением производственная функция y(е,q)[2].

В терминах производственной функции е является фактором производства. Входящая в модель переменная q – является случайным параметром, отражающим случайный (стохастический) характер модели, определяющим неконтролируемые факторы рынка. В качестве примера, рассмотрим производственную функцию для ситуации, когда принципалом является владелец ресторана, а агентом официант. Очевидно, что доход ресторана зависит от многих факторов, в том числе от усилий официанта. Можно ожидать, что чем больше усилий прикладывает официант, тем больше денег оставит посетитель. Этот факт можно математически отразить соотношением

dy/de >0

(1)

Введение случайной величины q в производственную функцию объясняется тем, что величина заказа в нашем примере зависит не только от усилий официанта, но и от усилий других лиц (прежде всего поваров, сомелье, хостесов и т.д.) и от состояния клиентов (их настроения, аппетита и др.). Поэтому, доход, который принесет данный клиент, есть величина случайная, но на её распределение оказывает влияние усилия (работа) официанта (в том числе). В общем случае можно утверждать, что (числовое) значение производственной функции зависит от состояния рынка.

Имеются нейтральный к риску принципал и избегающий риска агент. Это различие отражается в конкретном виде их функций полезности (см.приложение)

Функция полезности агента имеет следующий вид:

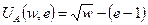	(2)
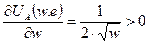	(3)
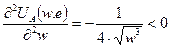	(4)

где 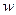— ставка заработной платы, 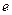— уровень усилий агента. Функция полезности агента вогнута, что является формальным признаком его рискофобии, т.е. у него есть склонность избегать риска.

Уровень усилий может принимать два значения, 1 и 2, которые далее будут обозначаться как «низкий» и «высокий» уровни усилий.

Альтернативная стоимость работы, определяемая рыночной ставкой заработной платы, такова, что её полезность равна 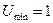. Это означает, что при любом реальном контракте средняя полезность для агента должна быть выше этого уровня 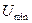(единицы), в противоположном случае он ищет работу в другом месте. Это предположение позволяет рассчитать минимальный уровень заработной платы, при условии, что агента прилагает «низкий» или «высокий» уровень усилий, а принципал знает об этом.

Если агент прилагает низкий» уровень усилий, то

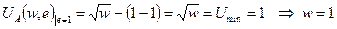(5)

Т.е. для того чтобы работник прилагал даже низкий уровень усилий, ему необходима заработная плата не ниже чем единица, иначе он может уйти работать в другое место.

Если агент прилагает «высокий» уровень усилий, то

.

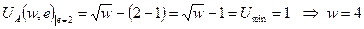(6)

Т.е. для того чтобы работник прилагал высокий уровень усилий, ему необходима заработная плата не ниже чем четыре единицы.

Полученную ситуацию можем проиллюстрировать следующим примером. Пусть агентом является преподаватель матметодов, принципалом – университет. Если преподаватель ведет занятия на русском языке, то он прилагает усилия на низком уровне и получает зарплату равную 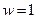. Если преподаватель ведет занятия на английском языке, то он прилагает усилия на высоком уровне и получает зарплату равную 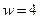. Очевидно, что во втором случае его уровень усилий существенно выше, как при подготовке занятий, так и при их проведении. Однако агент, несмотря на то, что уровень зарплаты в 4 раза выше во втором случае, он оценивает полезность (для себя) этих двух ситуаций одинаково.

Будем полагать, что доход принципала зависит от уровня усилий агента и внешних обстоятельств как это показано на рис.1 и 2. Будем полагать, что состояние рынка для простоты имеет два уровня и характеризуется как «удачный» или «неудачный» период для бизнеса.

Усилия работника	е=
Период			неудачный	удачный
Доход фирмы		R
Вероятность		P	2/3	1/3

Рис. 1. Случайная величина, определяющая доход принципала в зависимости от состояния рынка (удачности или неудачности периода) при низком уровне усилий агента.

Усилия работника	е=
Период			неудачный	удачный
Доход фирмы		R
Вероятность		P	1/3	2/3

Рис. 2. Случайная величина, определяющая доход принципала в зависимости от состояния рынка (удачности или неудачности периода) при высоком уровне усилий агента.

Сравнивая рис.1 и 2. можно увидеть, что вероятность более высокого дохода принципала возрастает при увеличении усилий агента.

Будем полагать, что ситуация многократно повторятся, т.е. сначала заключается контракт на какой-то длительный срок (год и т.п.), а внутри этого длительного срока рассматриваем множество отдельных периодов времени (день, неделя и т.д.), по итогам каждого происходит подведение промежуточных итогов. Т.е. проходит один период времени, в течение которого агент выполняет свои функции, прилагая тот или иной уровень усилий, далее по окончанию этого периода подводят итоги, выяснив, чему равен доход фирмы и (заодно) удачным или неудачным был прошедший период. После этого будет определен доход фирмы . Если период был удачным, то 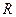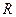равно 30, а если период был неудачным, то 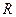равно 10. Важно то, что при высоком уровне усилий удачный период реализуется существенно чаще, чем при низком уровне усилий. Очевидно, что благополучие фирмы определяет не отдельный период, а общий результат многократного повторения производственного процесса. Затем подводим итог деятельности фирмы, сосчитав средний доход за период за весь длительный срок действия контракта. При этих данных можно рассчитать ожидаемый доход принципала при многократном повторении описанного выше производственного цикла, очевидно, что это величина будет равна математическому ожиданию соответствующей случайной величины.

Обозначим средний доход принципала при низком уровне усилий агента через .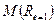

Вычислим это значение, пользуясь известными формулами из теории вероятности:

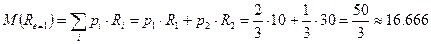(7)

Обозначим средний доход принципала при высоком уровне усилий агента через .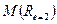

Вычислим это значение, пользуясь известными формулами из теории вероятности:

.

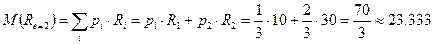(8)

Разница в доходах принципала при двух уровнях усилий агента очевидна, средний доход принципала при высоком уровне усилий агента будет выше, чем при низком.

Для лучшего понимания экономических последствий морального риска, сравним два случая, в одном из которых усилия агента наблюдаемы, т. е. проблема морального риска не возникает, а в другом усилия агента не поддаются наблюдению и у него появляется возможность проявить оппортунистическое поведение, т. е. встает проблема морального риска.

Будем полагать, что функцией полезности 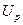для принципала является величина чистого дохода, т.е. величина дохода минус величина вознаграждения агента .

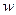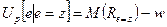(9)

где 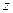- уровень усилий агента.