Преобразование информации с помощью автоматов
Оглавление
Введение.. 3
1 Преобразование информации с помощью автоматов 4
2 Синтез автомата Мура.. 7
3 Синтез автомата Мили.. 14
Литература.. 19
Приложение. Варианты заданий. 20
Введение
Данная разработка представляет собой методическое пособие по дисциплине «Электронные промышленные устройства» — одному из важнейших компонентов федерального государственного образовательного стандарта по направлению «Электроника и микроэлектроника». Изучение этой дисциплины основано на знаниях полученных студентами в процессе изучения на ранних курсах схемотехники и системотехники. Дисциплина позволяет формировать знания и умения, необходимые для корректной постановки и решения проблем в области информатики, схемотехники при создании вычислительных структур, алгоритмов и программ обработки информации.
Работы в области теории автоматов начались в середине 50-х годов прошлого века. Моделирование конечного автомата при разработке устройств в области информатики и других областях инженерной деятельности является удобным средством, позволяющим разработчикам реализовывать алгоритмы работы в схемотехнические решения.
Таким образом, теория автоматов является одним из основных инструментов в современной теоретической и практической информатике, системотехнике и при проектировании систем логического управления. При разработке систем логического управления станком с ЧПУ, промышленным роботом, обрабатывающим центром, гибким модулем и т.д. в зависимости от используемой элементной базы проектировщику необходимо оптимизировать проектные решения по различным критериям качества. При аппаратной реализации алгоритмов управления в качестве критерия качества выступает объем элементной базы, стоимость, надежность.
Теория автоматов является фундаментом большого числа разнообразных приложений от языковых процессоров до систем управления реального времени и протоколов связи. Простейшими конечными автоматами являются автоматы Мура и Мили, изучением которых посвящена данная разработка.
Преобразование информации с помощью автоматов
Преобразование информации в виде вход 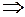 выходзависит не только от входной информации, но и от предыстории преобразования. Например, один и тот же вход — извинения пассажира после того, как он наступил другому пассажиру на ногу в троллейбусе — вызовет у него одну реакцию в первый раз и совсем другую — в третий или четвертый раз. Реакция пассажира будет различной и будет зависеть от предыдущих событий и от входной истории. Таким образом, существуют функциональные преобразователи информации, в которых выходной сигнал зависит не только от входного сигнала в данный момент, но и от входной истории [1].
выходзависит не только от входной информации, но и от предыстории преобразования. Например, один и тот же вход — извинения пассажира после того, как он наступил другому пассажиру на ногу в троллейбусе — вызовет у него одну реакцию в первый раз и совсем другую — в третий или четвертый раз. Реакция пассажира будет различной и будет зависеть от предыдущих событий и от входной истории. Таким образом, существуют функциональные преобразователи информации, в которых выходной сигнал зависит не только от входного сигнала в данный момент, но и от входной истории [1].
Для нормального функционирования автомат должен иметь запоминающее устройство для запоминания состояний. Т.к. состояние автомата является эквивалентной предысторией входного сигнала, состояние может измениться только при приходе очередного входного сигнала. Функционирование автомата можно представить графически. На рис. 1 показан автоматный преобразователь и его реализация.
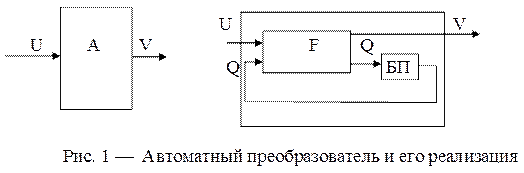
Блок памяти автомата хранит информацию о текущем состоянии Q, а следующее состояние определяется входным сигналом U и текущим состоянием, а выходная реакция автомата обозначена V. Блок F на основе входных сигналов и предыдущих состояний формирует очередное состояние Q.
Из выше отмеченного следует, что автоматный преобразователь или управляющий автомат определяется:
1. Множеством выходных сигналов
V= {V1, V2, …, Vm},
соответствующих множеству состояний автомата. При Vi =1 исполняется i-я микрооперация.
2. Множеством входных сигналов
U = {U1, U2, …, Un},
соответствующих входной истории.
3. Множеством подлежащих реализации микропрограмм.
4. Множеством состояний
Q = {Q0, Q1, …, Qr},
Таким образом, мы имеем дело не с функциональными преобразователями информации, а с преобразователями, в которых реакция или выходной сигнал зависит не только от входа в данный момент, но и от входной истории (предыдущего состояния).
Автоматный преобразователь может быть задан как автомат Мура
Q(t+1) = A[Q(t), U1(t), U2(t), … Un(t)];
V1(t) = B1[Q(t)];
………………………………………….
Vm(t) = Bm[Q(t)];
или автомат Мили
Q(t+1) = A[Q(t), U1(t), U2(t), … Un(t)];
V1(t) = B1[Q(t), U1(t), U2(t), …, Un(t)];
………………………………………...
Vm(t) = Bm[Q(t), U1(t), U2(t), …, Un(t)].
A и B функции переходов и выходов определяются заданной микропрограммой.
Таким образом, управляющий автомат может быть задан как автомат Мура или Мили, но у них есть отличия, заключающиеся в том, что у автомата Мура выходные сигналы вырабатываются в зависимости от внутреннего состояния автомата, а у автомата Мили выходные сигналы зависят от внутреннего состояния и от входных сигналов. Состояние любого автомата обусловливается его предыдущим состоянием и входными сигналами:
Q(t+1) = A[Q(t), U1(t), U2(t), …, Un(t)],
где Q(t) — предыдущее состояние автомата,
Q(t+1) — следующее состояние,
Существуют два основных метода построения логики управляющих автоматов.
1. Управляющий автомат с «жесткой» или схемной логикой. В этом методе каждой операции строится набор комбинационных схем. Чтобы изменять алгоритм работы автомата необходимо каждый раз изменять набор комбинационных схем.
2. Управляющий автомат с хранимой в памяти логикой (с запоминаемой или программируемой логикой). Здесь каждой выполняемой в цифровом устройстве операции ставится в соответствие совокупность хранимых в памяти микрокоманд.
Структурная схема автомата с «жесткой» логикой приведена на рис. 2
В состав схемы входят регистр кода операции (часть регистра команд), счетчик тактов, дешифраторы тактов и кода операции, а также блок логических схем и формирователей управляющих сигналов.
От блока синхронизации сигналы поступают на счетчик тактов, на выходе которого в двоичном коде представлены номера тактов от 1 до n. Дешифратор тактов формирует на j-м выходе сигнал при i-м состоянии счетчика тактов (во время i-го такта). Дешифратор кода операции выдает сигнал на j-м выходе, при исполнении j-той команды. Логические схемы и формирователи управляющих сигналов вырабатывают управляющие сигналы для выполнения требуемых в данном такте микроопераций.

Управляющие автоматы с хранимой в памяти логикой используют принцип микропрограммного управления. В данном случае управляющие сигналы записываются в специальную память микропрограмм, построенную на перепрограммируемом или постоянном запоминающих устройствах. Для выбора конкретной управляющей программы в коде операции в определенном виде указывается адрес микропрограммы.
Рассмотрим синтез и работу автоматов Мура и Мили.
Синтез автомата Мура
Под синтезом алгоритма управления понимается одна из основных задач проектирования устройств и систем управления, состоящая в нахождении комплекса логических процедур, приводящих к построению логической схемы. Алгоритм может быть представлен графически в виде блок-схемы или микропрограммного графа.
На рис. 3 показана блок-схема, на рис. 4 — граф микропрограммного автомата в качестве примера реализации данного устройства.
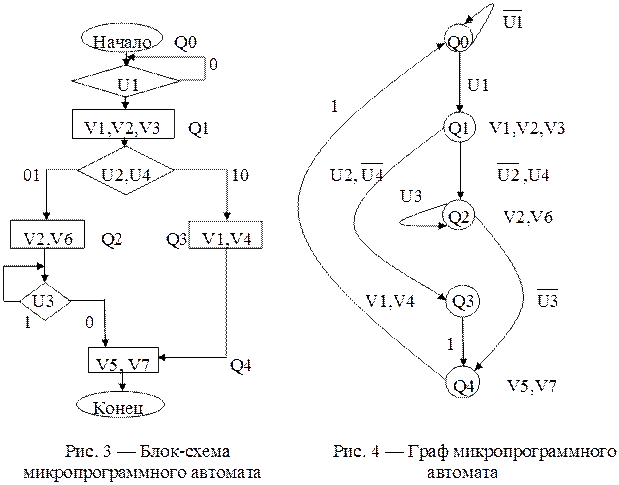
На рисунках обозначены входные сигналы автомата символами U1, U2, U3, выходные сигналы символами V1, V2, V3, V4, V5, V6, V7, внутренние состояния Q0, Q1, Q2, Q3, Q4. Исходное состояние Q0 должно устанавливаться при подаче питающего напряжения и после окончания работы микропрограммы т.е. необходима начальная установка. Рассматриваемый автомат, находится в исходном состоянии до появления входного сигнала U1. После появления сигнала U1 автомат переходит в состояние Q1 и вырабатываются выходные сигналы V1, V2 и V3. В зависимости от сигналов U2 и U4, т.е. при воздействии сигналов 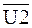 и U4 автомат переходит в состояние Q2, а при сигналах U2 и
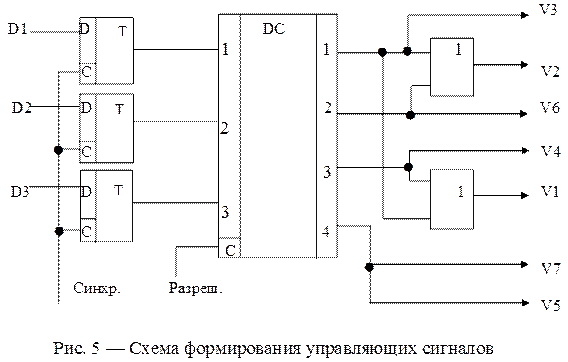
и U4 автомат переходит в состояние Q2, а при сигналах U2 и 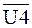 в состояние Q3. Каждому состоянию соответствует определенный набор выходных сигналов: в состоянии Q2 вырабатываются сигналы V2 и V6, при Q3 — V1 и V4 и при Q4 — V5 и V7. Из состояния Q2 в состояние Q4 автомат переходит под воздействием сигнала U3 и переходит в состояние Q4 при воздействии сигнала
в состояние Q3. Каждому состоянию соответствует определенный набор выходных сигналов: в состоянии Q2 вырабатываются сигналы V2 и V6, при Q3 — V1 и V4 и при Q4 — V5 и V7. Из состояния Q2 в состояние Q4 автомат переходит под воздействием сигнала U3 и переходит в состояние Q4 при воздействии сигнала  . Если сигнал U3 присутствует (левая петля U3) автомат не меняет своего состояния и сигналы V2 и V6 продолжают вырабатываться. И если сигнал U3 отсутствует, то происходит переход в состояние Q4. В состояние Q4 происходит переход из состояний Q2 и Q3, из Q2 в Q4 переход по условию, а из Q3 в Q4 — безусловный и происходит переход под воздействием тактового сигнала. Безусловный переход происходит также из состояния Q4 в состояние Q0. Состояния Q0 и Q4 являются одним и тем же состоянием и являются исходным состоянием.
. Если сигнал U3 присутствует (левая петля U3) автомат не меняет своего состояния и сигналы V2 и V6 продолжают вырабатываться. И если сигнал U3 отсутствует, то происходит переход в состояние Q4. В состояние Q4 происходит переход из состояний Q2 и Q3, из Q2 в Q4 переход по условию, а из Q3 в Q4 — безусловный и происходит переход под воздействием тактового сигнала. Безусловный переход происходит также из состояния Q4 в состояние Q0. Состояния Q0 и Q4 являются одним и тем же состоянием и являются исходным состоянием.
Продолжим процесс синтеза автомата Мура. Данный автомат имеет пять состояний с Q0 по Q4. Для запоминания этих состояний схема должна содержать память соответствующей разрядности. Такую память удобно строить на D триггерах. Число триггеров определяется по формуле:
K = log2r
где K — число триггеров;
r — число состояний.
Так как число состояний у автомата равно пяти, то число триггеров равно трем.
В табл. 1 сведем состояния триггеров памяти для хранения состояний автомата.
Таблица 1
| Состояние автомата | С о с т о я н и е т р и г г е р о в | ||
| Триггер 1 | Триггер 2 | Триггер 3 | |
| Q0 | |||
| Q1 | |||
| Q2 | |||
| Q3 | |||
| Q4 |
Теперь можно синтезировать схему для формирования выходных сигналов автомата. По логике схема должна содержать три D-триггера для хранения состояний, дешифратор для выделения состояний и логику формирования выходных сигналов. Логика строится по правилам: если управляющий сигнал V1 формируется при состояниях Q1 и Q3, то можно записать, что V1 = Q1 или Q3, что тоже самое V1 = Q1+Q3, соответственно для других сигналов:
V2=Q1+Q2,
V3=Q1,
V4 = Q3,
V5 = Q4,
V6 = Q2,
V7 = Q4.
Синтезированная схема формирования управляющих сигналов приведена на рис. 5
Для построения логической схемы управления триггерами хранения соответствующих состояний необходимо иметь следующие данные: состояние автомата в зависимости от состояния триггеров, последовательность состояний автомата согласно микропрограммы (рис. 3), условия перехода из предыдущего состояния в последующее. Теперь построим основную таблицу для синтеза автомата Мура.

 Таблица 2
Таблица 2
| Исх. состоя- ния | Исходные состояния триггеров | Сост. триггеров после перехода | Условия перехода | Сигналы на D входах триггеров | ||||||
| Тг1 | Тг2 | Тг3 | Тг1 | Тг2 | Тг3 | D1 | D2 | D3 | ||
| Q0 | 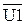 | |||||||||
| Q0 | U1 | |||||||||
| Q1 |  U4 U4 | |||||||||
| Q1 | U2  | |||||||||
| Q2 | 1 ` | U3 | ||||||||
| Q2 |  | |||||||||
| Q3 | ||||||||||
| Q4 |
По порядку слева направо обозначение столбцов следующее: состояние автомата до перехода в другое состояние, состояние триггеров памяти до перехода, состояние триггеров после перехода, условия перехода из исходного состояния в следующее состояние. Если переход условный, и в переходе участвуют несколько сигналов, то записывается конъюнкция этих сигналов, а если переход безусловный, т.е. входные сигналы не участвуют в организации перехода — в данной строке ставится единица. В последних колонках записываются значения сигналов на D входах триггеров. Т.к. с приходом синхронизирующего импульса входной сигнал со входа D переписывается на выход триггера, то колонки «Состояние триггеров после перехода» и «Сигналы на D входах триггеров» совпадают. Первая строка таблицы говорит о том, что автомат остается в исходном состоянии т.к. входной сигнал U1отсутствует. Вторая строка свидетельствует о том, что с приходом сигнала U1 автомат из нулевого состояния перейдет в первое. Аналогично рассуждая заполняется оставшаяся часть таблицы. После разработки таблицы выбираем строки с единичным значением входных сигналов триггеров и записываем функции возбуждения с помощью уравнений. Для входа D1 выбираем шестую и седьмую строки, входа D2 третью, четвертую и пятую строки, а для D3 вторую и четвертую строки. Теперь можно записать дизъюнкцию конъюнкций исходных значений автомата и условия перехода:

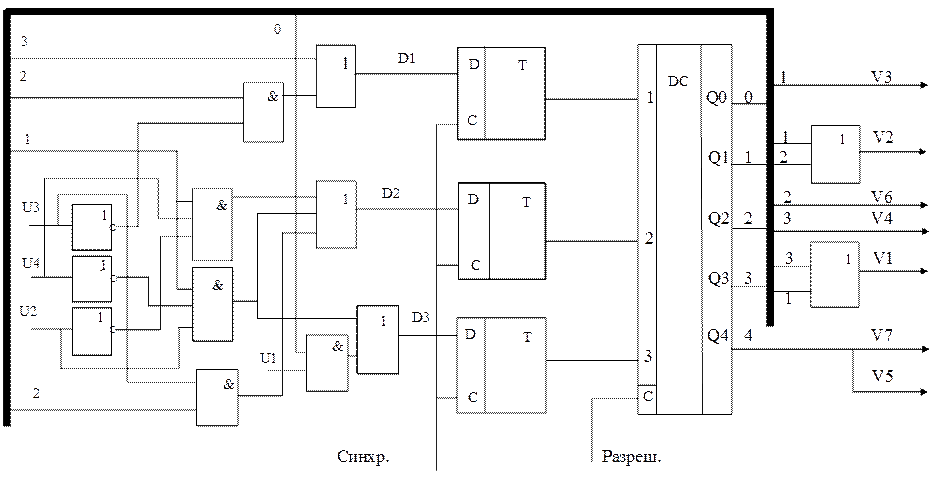
Рис. 6 — Полная схема автомата
D1 = Q2  + Q3,
+ Q3,
D2 = Q1 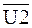 U4 + Q1U2
U4 + Q1U2 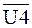 + Q2U3,
+ Q2U3,
D3 = Q0U1 + Q1U2 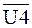 .
.
Перед построением схемы возбуждения полученные выражения D1, D2 и D3 необходимо минимизировать (если в этом есть необходимость). Например (А + 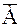 ) = 1 из Булевой алгебры. Теперь построим логическую схему для получения D1, D2 и D3, соединим ее со схемой на рис. 5 и получим полную схему автомата, реализующую алгоритм приведенный на рис. 6.
) = 1 из Булевой алгебры. Теперь построим логическую схему для получения D1, D2 и D3, соединим ее со схемой на рис. 5 и получим полную схему автомата, реализующую алгоритм приведенный на рис. 6.
Синтез автомата Мили
Из выражений для автомата Мура и Мили (раздел 1) видно, что у автомата Муры выходные сигналы зависят только от состояния, а у автомата Мили от состояния и входных сигналов. Для синтеза автомата Мили используем ту же микропрограмму, что и для автомата Мура. Микропрограмма автомата Мили приведена на рис. 7, а граф микропрограммы показан на рис. 8
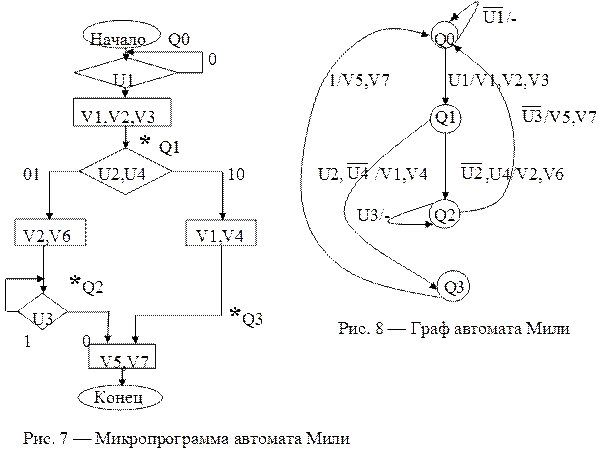
Начальные рассуждения при синтезе автомата Мили такие же как при построении автомата Мура. Есть некоторое отличие в представлении состояний. Как и автомата Мура сигнал U1 является начальным. При появлении сигнала U1 сразу же на выходе формируются выходные сигналы V1,V2 и V3 и в формировании выходных сигналов принимают участие предыдущее состояние автомата Q0 и входной сигнал U1. При поступлении сигнала U1 и при воздействии синхроимпульса, поступающего на синхронизирующий вход триггеров памяти автомат переходит в следующее состояние Q1. Состояние Q1 отмечается звездочкой рядом с дугой, а не напротив блока с сигналами V1, V2 и V3 как у автомата Мура.
После состояния Q1 происходит условный переход в зависимости от сигналов U2 и U4: при сигналах 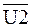 и U4 вырабатываются сигналы V2 и V6 и при воздействия синхроимпульса автомат переходит в состояние Q2, при этом управляющие сигналы не вырабатываются. Если значение входного сигнала U3 станет равным нулю, тогда в этой ветви появятся сигналы V5 и V7, а с приходом синхроимпульса автомат переходит в состояние Q0 (исходное состояние). При U2 и
и U4 вырабатываются сигналы V2 и V6 и при воздействия синхроимпульса автомат переходит в состояние Q2, при этом управляющие сигналы не вырабатываются. Если значение входного сигнала U3 станет равным нулю, тогда в этой ветви появятся сигналы V5 и V7, а с приходом синхроимпульса автомат переходит в состояние Q0 (исходное состояние). При U2 и 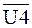 (правая ветвь) вырабатываются сигналы V1, V4 и с приходом синхросигнала автомат переходит в состояние Q3 с выработкой сигнала V5 и V7. Если внимательно посмотреть на рисунок 7, то можно увидеть, что у автомата Мили на одно состояние меньше, чем у автомата Мура. Значит у автомата Мили число состояний равно трем с Q0 по Q3 и для хранения этих состояний достаточно двух триггеров. Кодировка состояний представлена в таблице 3.
(правая ветвь) вырабатываются сигналы V1, V4 и с приходом синхросигнала автомат переходит в состояние Q3 с выработкой сигнала V5 и V7. Если внимательно посмотреть на рисунок 7, то можно увидеть, что у автомата Мили на одно состояние меньше, чем у автомата Мура. Значит у автомата Мили число состояний равно трем с Q0 по Q3 и для хранения этих состояний достаточно двух триггеров. Кодировка состояний представлена в таблице 3.
Таблица 3
| Состояние автомата | Состояние триггеров | |
| Т 1 | Т 2 | |
| Q0 | ||
| Q1 | ||
| Q2 | ||
| Q3 |
Функции выходов в соответствии с ранее приведенными правилами будут иметь вид:
V1 = Q0U1 + Q1U2 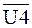 ,
,
V2 = Q0U1 + Q1 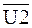 U4,
U4,
V3 = Q0U1,
V4 = Q1U2 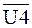 ,
,
V5 = Q2  + Q3,
+ Q3,
V6 = Q1 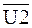 U4,
U4,
V7 = Q2  + Q3.
+ Q3.
Схема формирования сигналов управления для автомата Мили показана на рисунке 9.
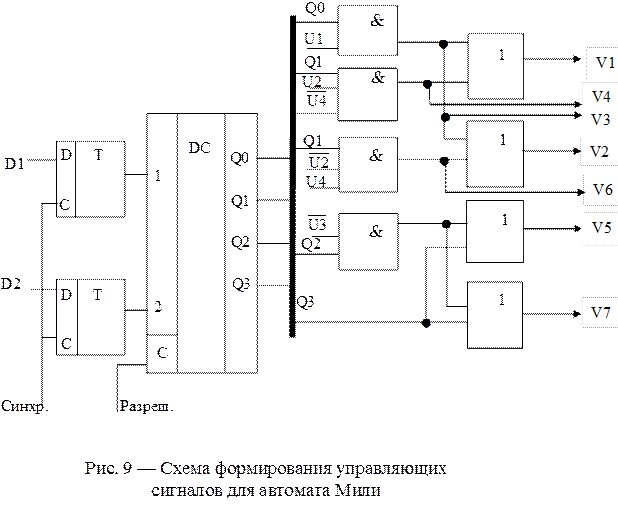
Составим таблицу 4 аналогично таблице 2
Таблица 4
| Исходное состояние автомата | Состояние триггеров до перехода | Состояние триггеров после перехода | Условия перехода | Состояния на D входах триггеров | |||
| Т1 | Т2 | Т1 | Т2 | D1 | D2 | ||
| Q0 | 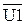 | ||||||
| Q0 | U1 | ||||||
| Q1 | 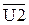 U4 U4 | ||||||
| Q1 | U2  | ||||||
| Q2 | U3 | ||||||
| Q2 | 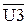 | ||||||
| Q3 |
Используя данные таблицы 4 запишем уравнения для формирования сигналов на D входах триггеров.
D1 = Q1 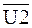 U4 + Q1U2
U4 + Q1U2  + Q2U3,
+ Q2U3,
D2 = Q0U1 + Q1U2  .
.
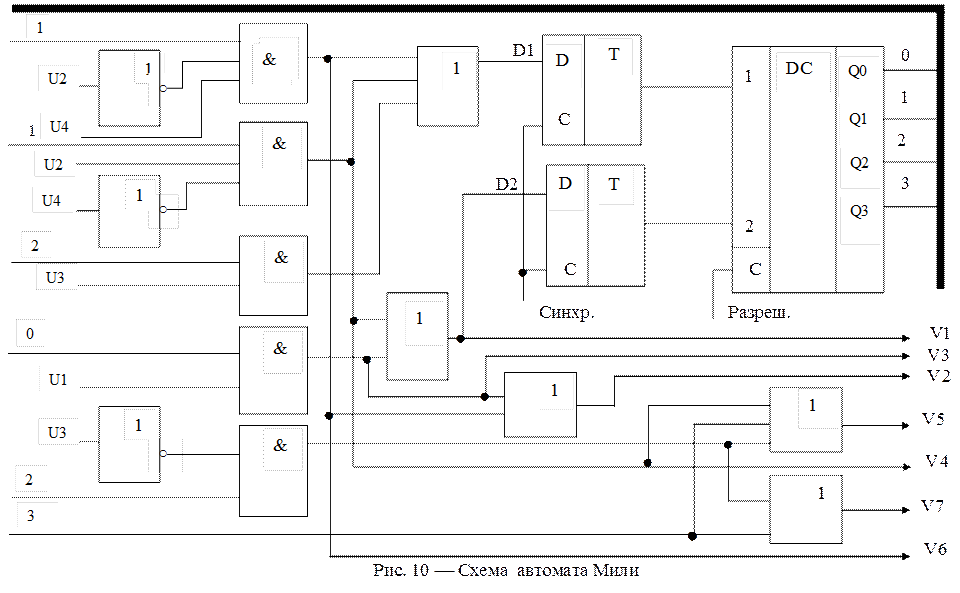
Используя все полученные данные построим схему автомата Мили — рис. 10

Литература
1. Карпов Ю.Г. Теория автоматов. — СПб.: Питер, 2002. — 224 с.: ил.
2. Каган Б.М. Электронные вычислительные машины и системы: Учеб. пособие для вузов. — 3-е изд., перераб. и доп. — М.: Энергоатомиздат, 1991. — 952 с.: ил.
3. Власов А.И., Сулимов Ю.И. Электронные промышленные устройства: Учеб. пособие. — Томск: Изд-во Том. гос. ун-та систем упр. и радиоэлектроники, 2004 — 286 с.
Приложение
Варианты заданий
Вариант 1
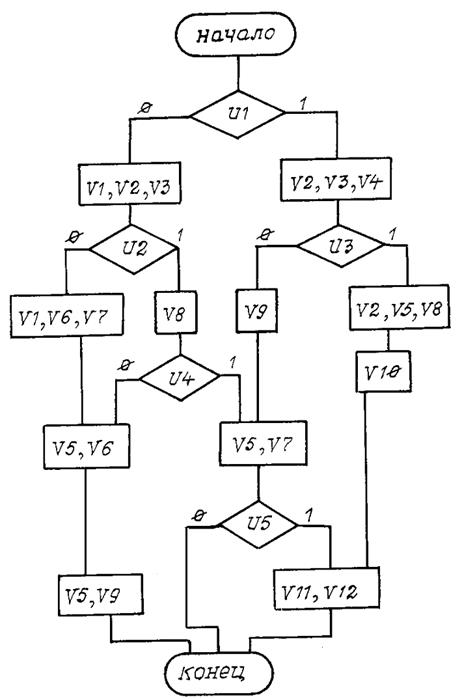
Рис. П1
Вариант 2
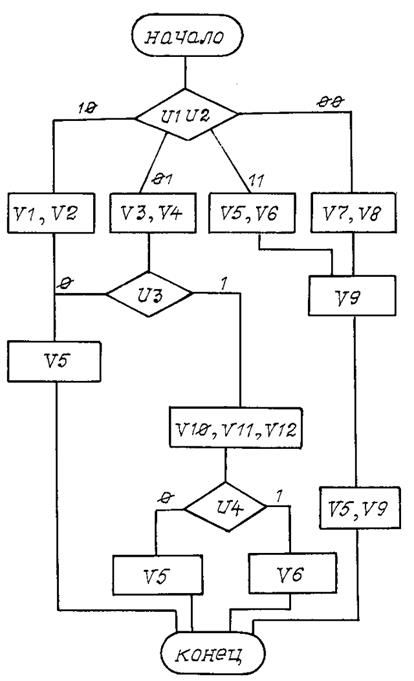
Рис. П2
Вариант 3

Рис. П3
Вариант 4
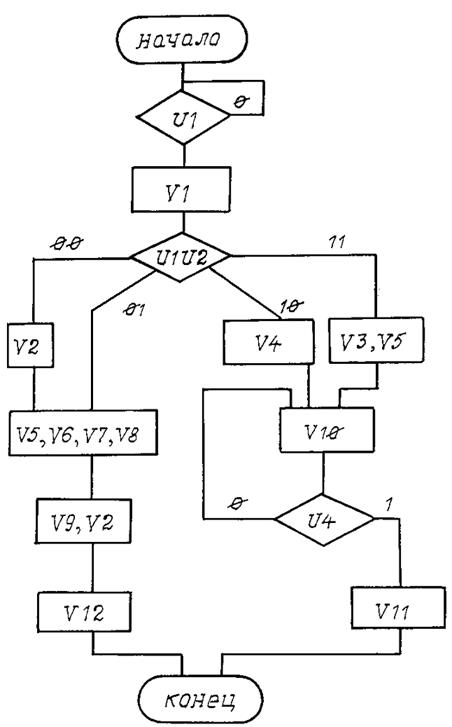
Рис. П4
Вариант 5
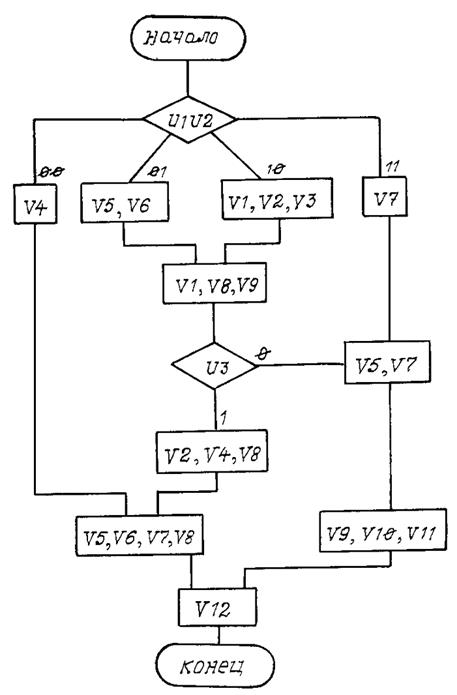
Рис. П5
Вариант 6
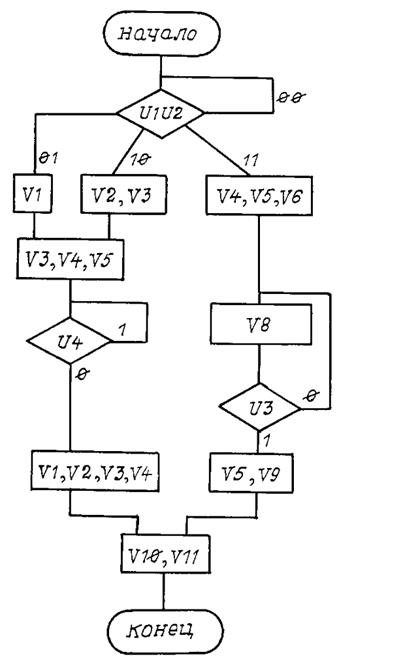
Рис. П6
Вариант 7
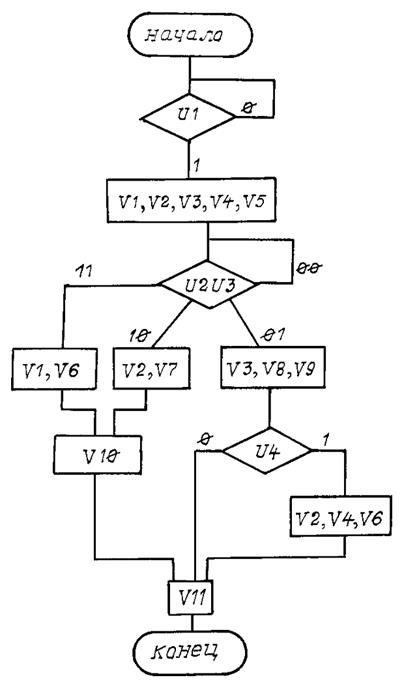
Рис. П7
Вариант 8
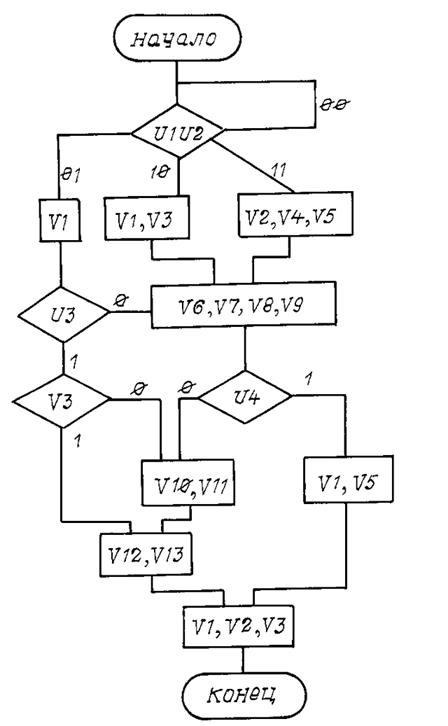
Рис. П8
Вариант 9
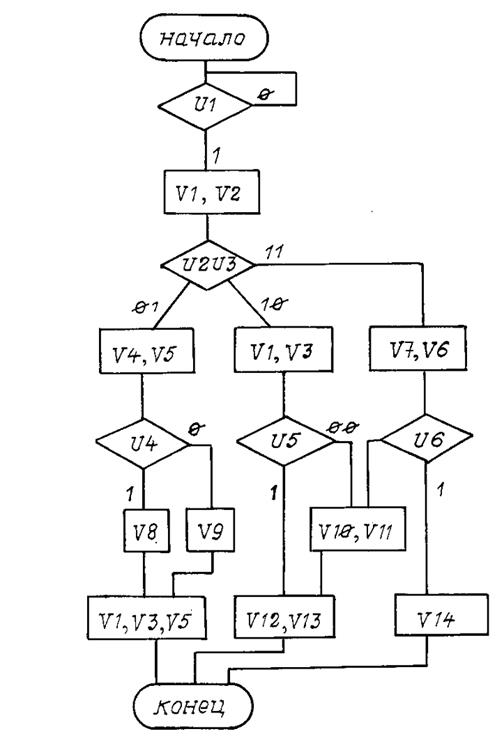
Рис. П9
Вариант 10
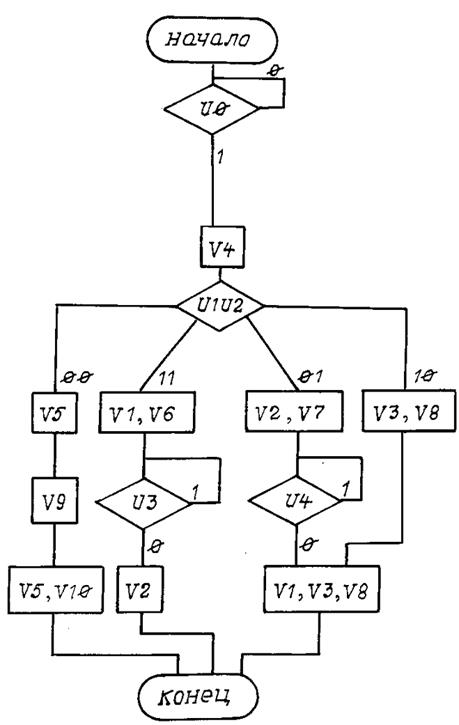
Рис. П10
Вариант 11
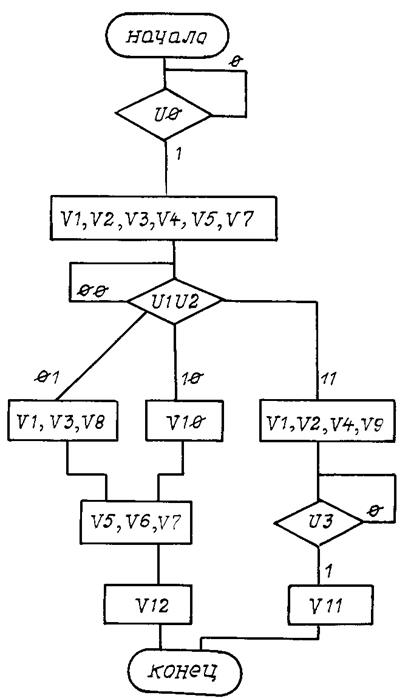
Рис. П11
Вариант 12
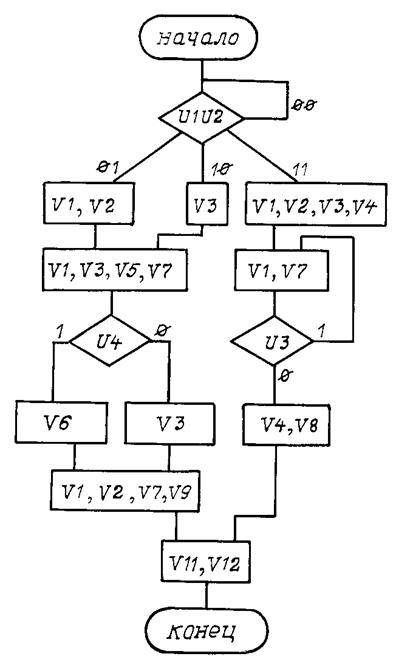
Рис. П12
Вариант 13
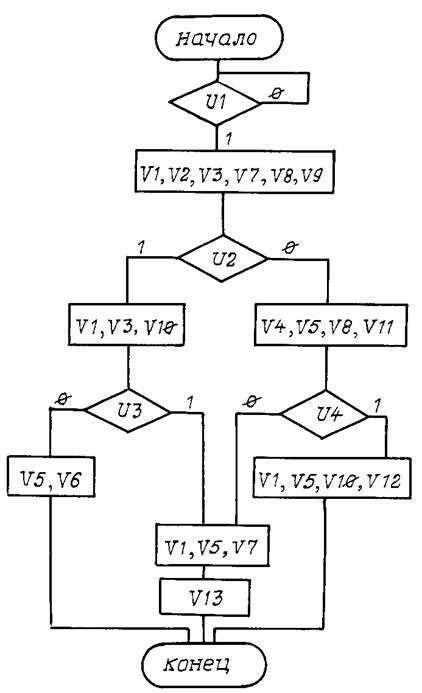
Рис. П13
Вариант 14
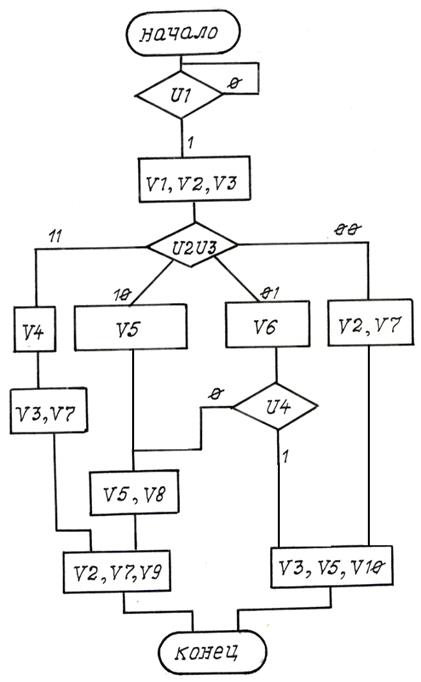
Рис. П14
Вариант 15

Рис. П15
Вариант 16
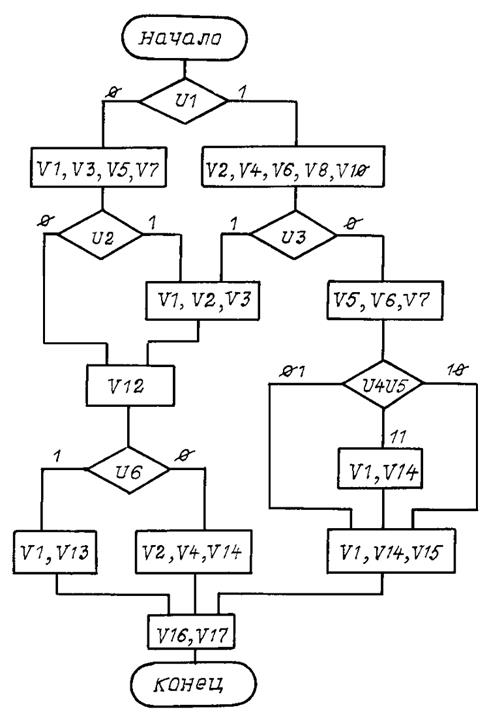
Рис. П16
Вариант 17
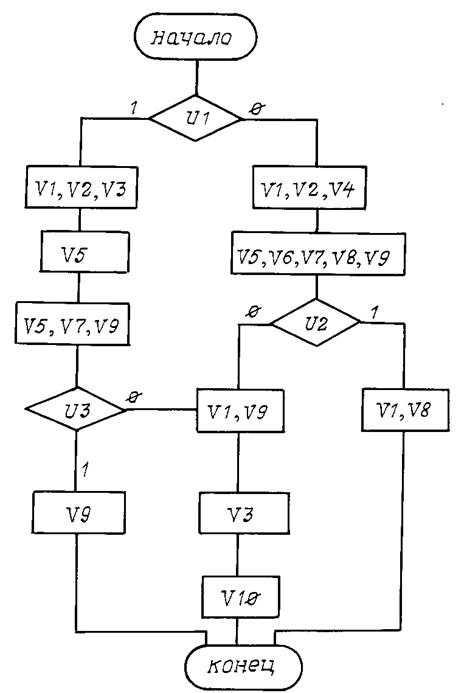
Рис. П17
Вариант 18
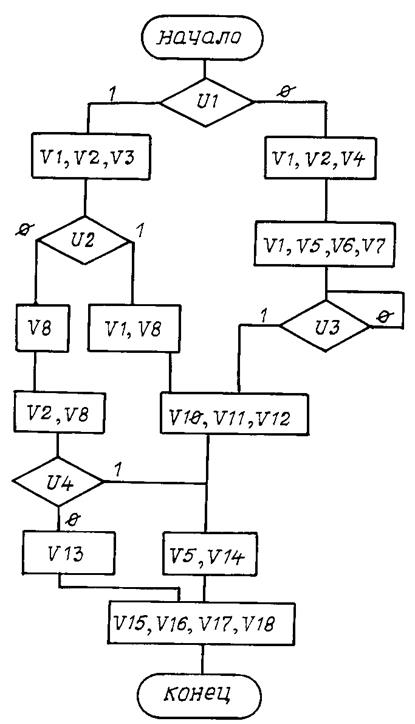
Рис. П18
Вариант 19
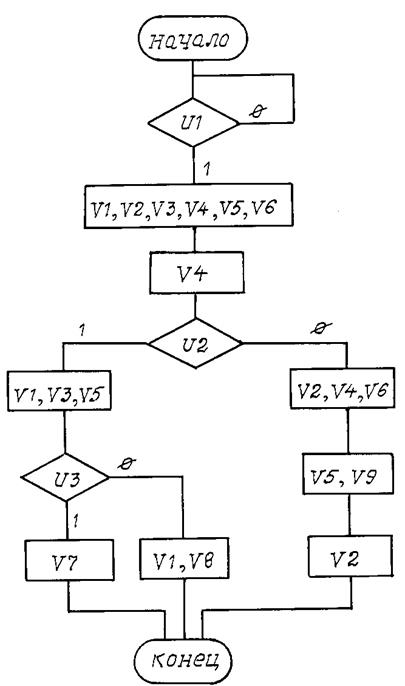
Рис. П19
Вариант 20
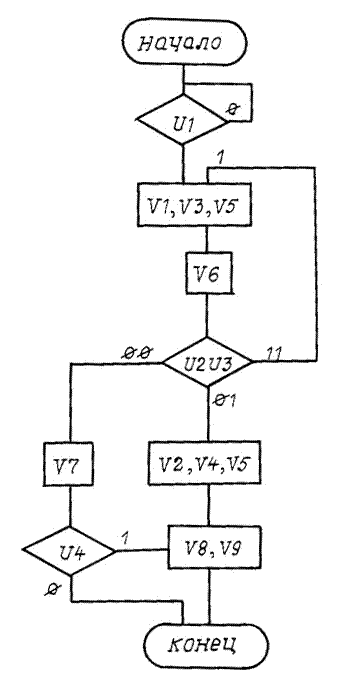
Рис. П20
Вариант 21
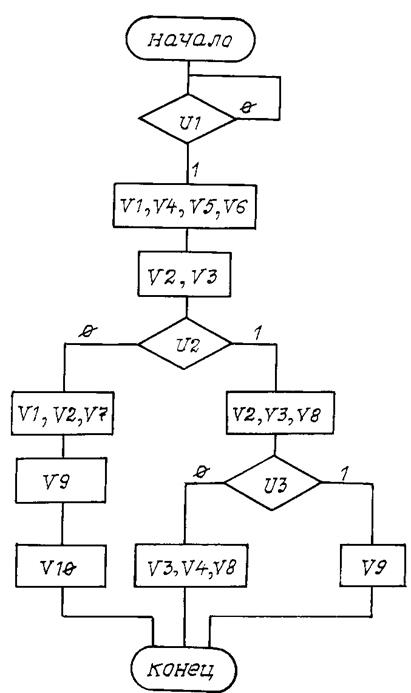
Рис. П21
Вариант 22
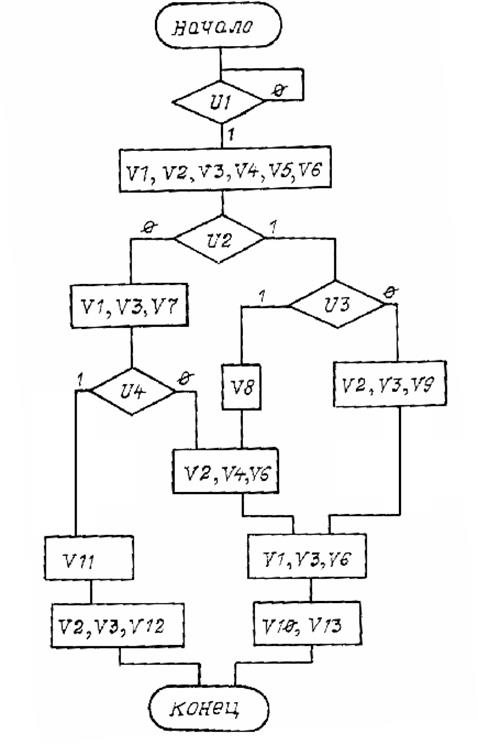
Рис. П22
Вариант 23
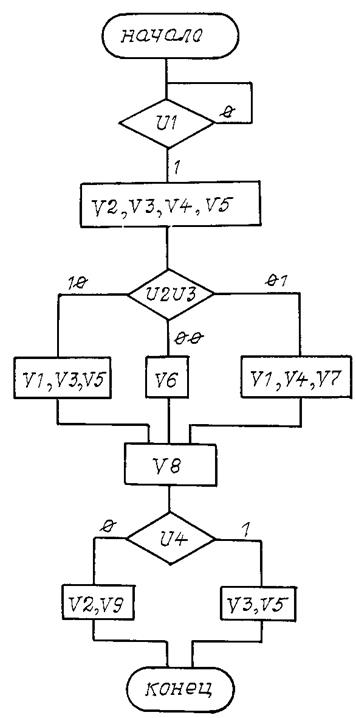
Рис. П23
Вариант 24
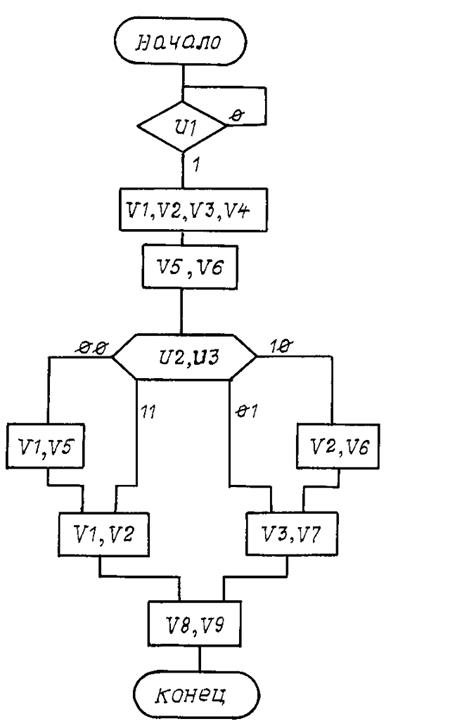
Рис. П24
Вариант 25
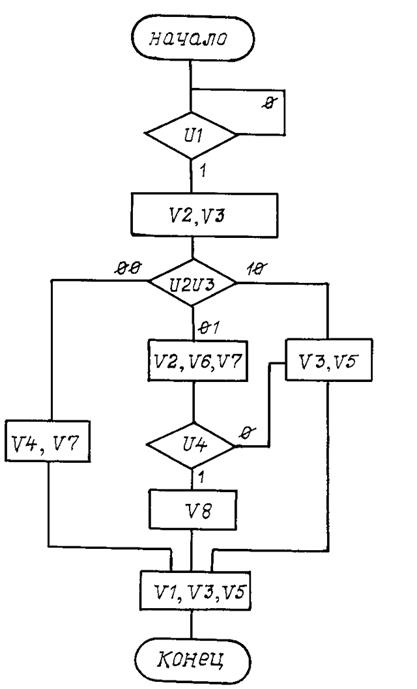
Рис. П25
Вариант 26
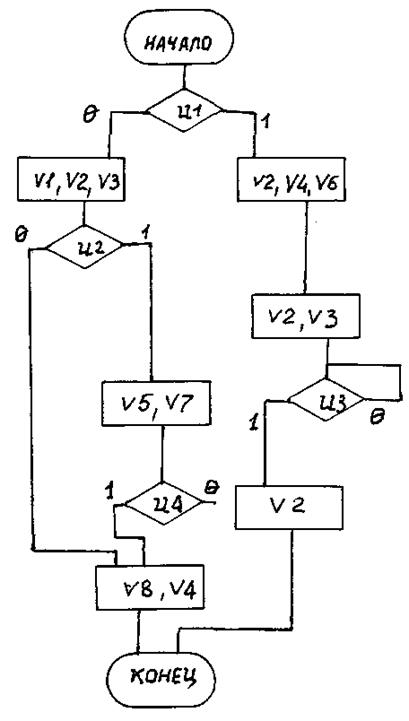
Рис. П26
Вариант 27
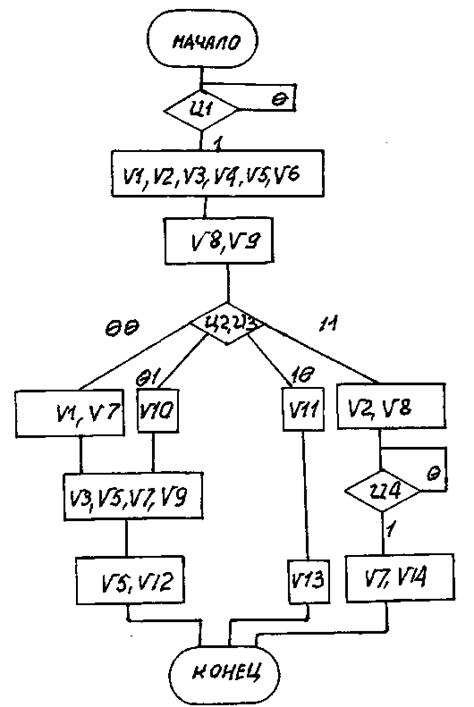
Рис. П27
Вариант 28
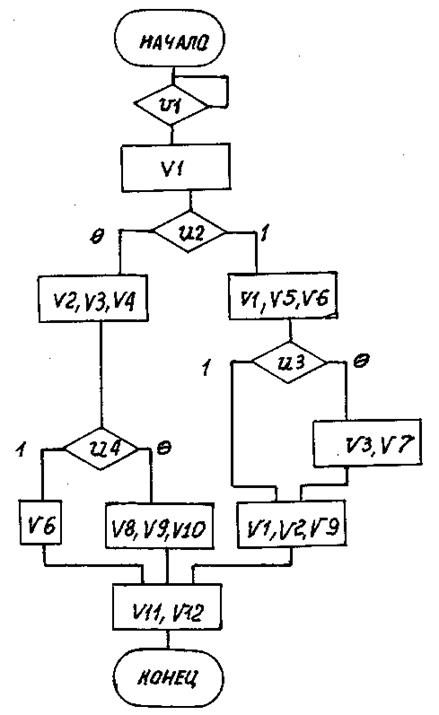
Рис. П28
Вариант 29
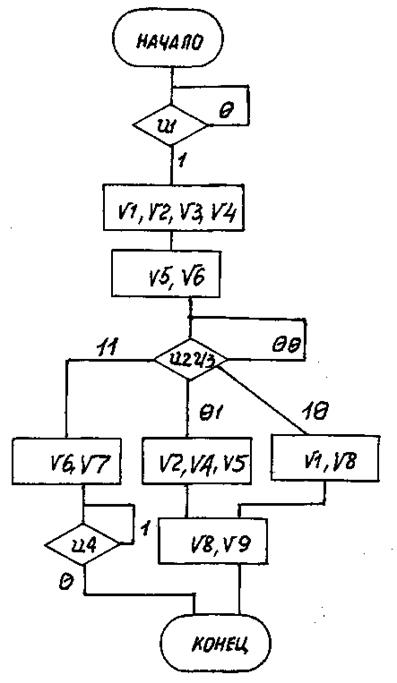
Рис. П29
Вариант 30
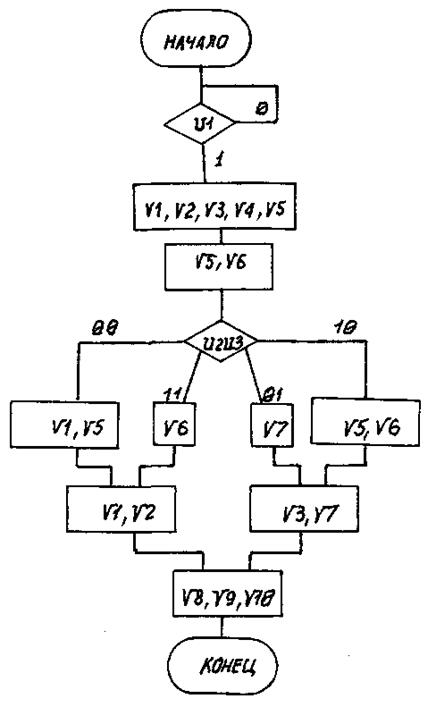
Рис. П30
Вариант 31
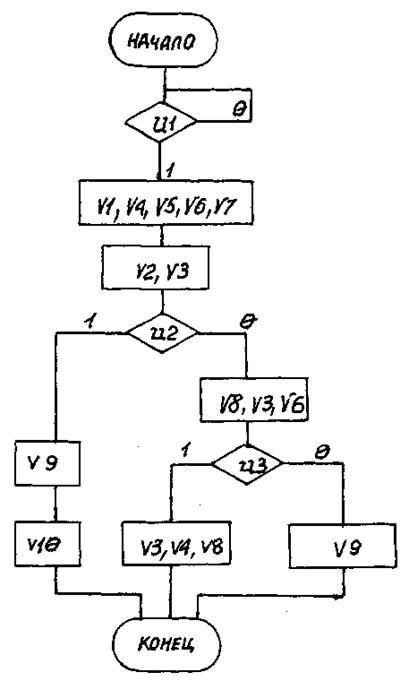
Рис. П31
Вариант 32
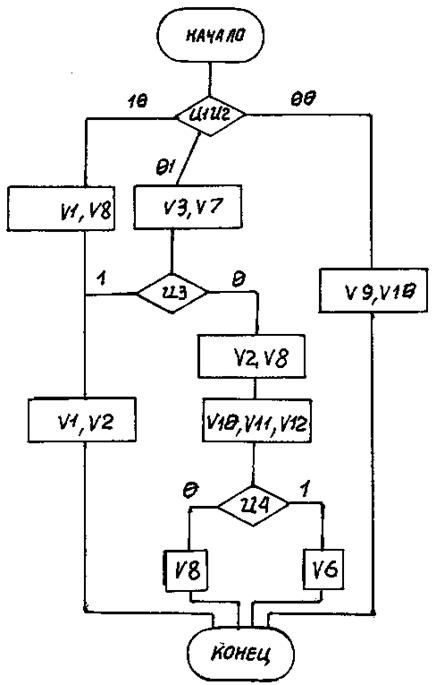
Рис. П32
Вариант 33
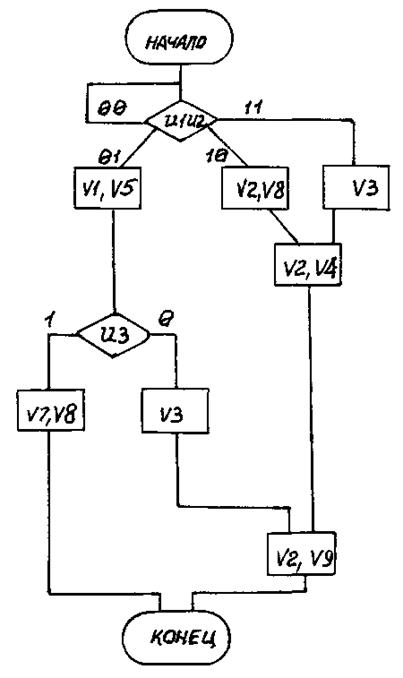
Рис. П33
Вариант 34
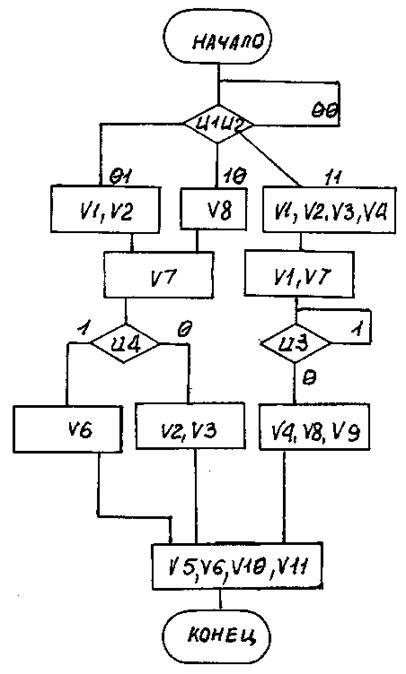
Рис. П34
Вариант 35
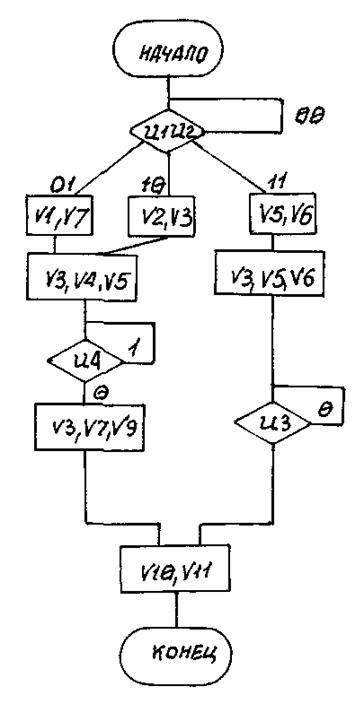
Рис. П35
Вариант 36
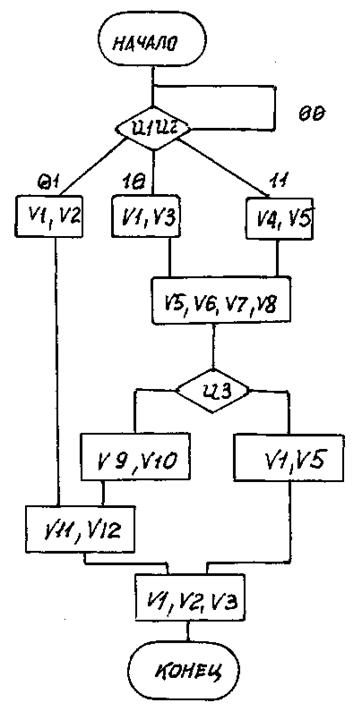
Рис. П36
Вариант 37
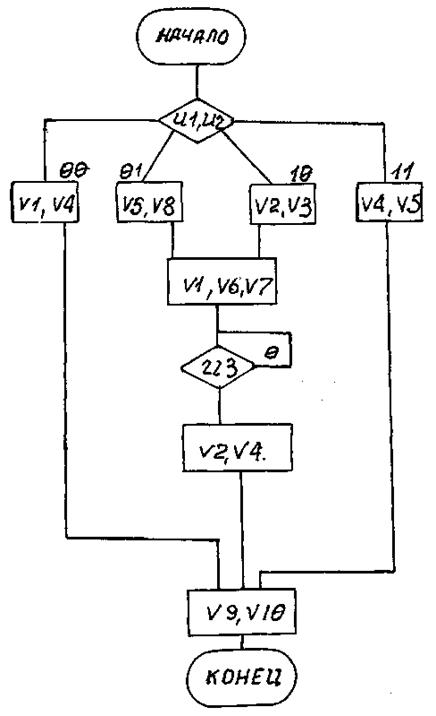
Рис. П37
Вариант 38
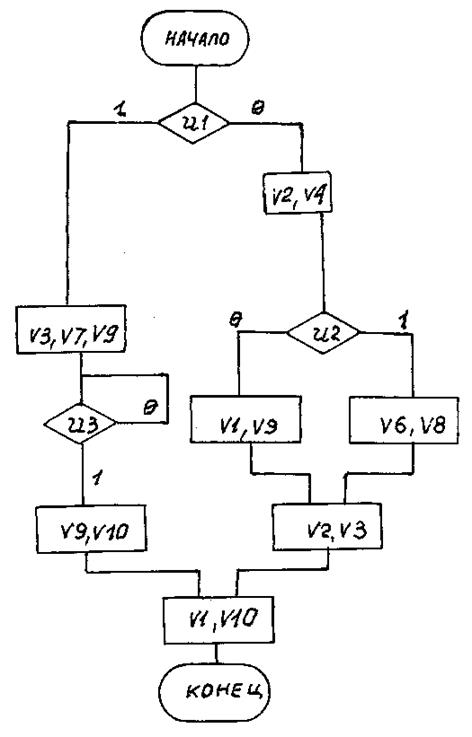
Рис. П38
Вариант 39
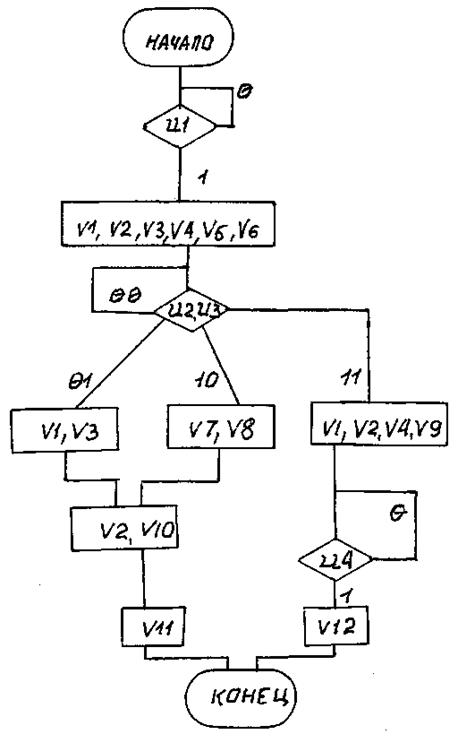
Рис. П39
Вариант 40
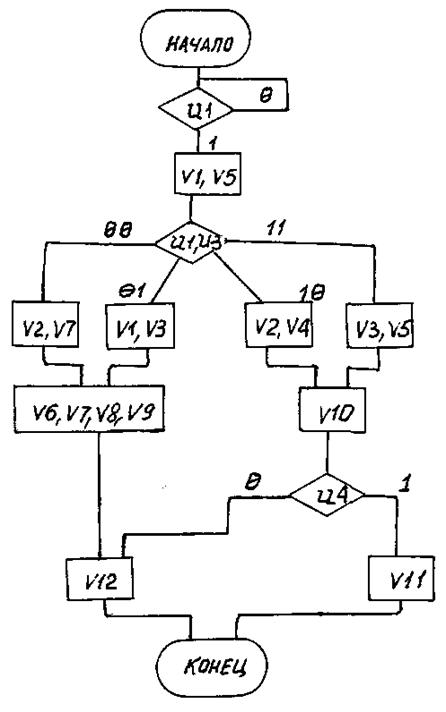
Рис. П40
Вариант 41
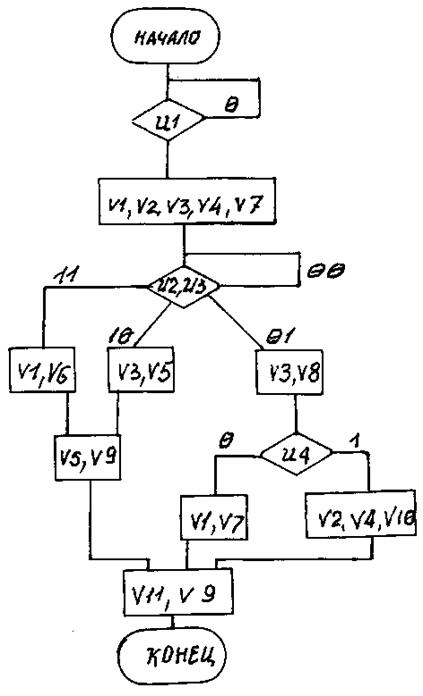
Рис. П41
Вариант 42
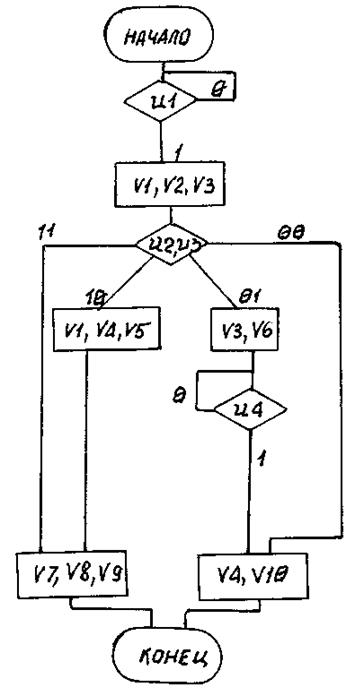
Рис. П42
Вариант 43

Рис. П43
Вариант 44
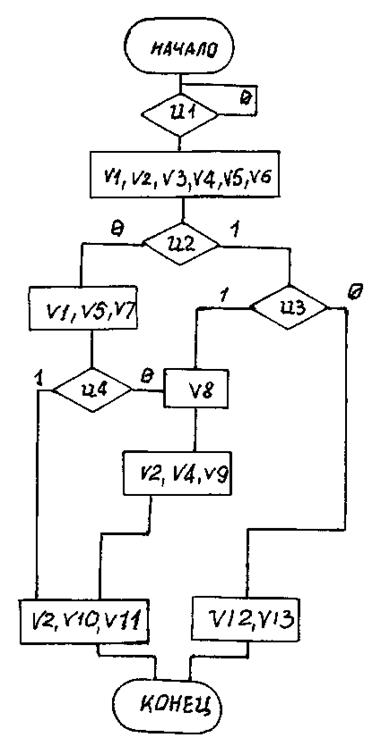
Рис. П44
Вариант 45
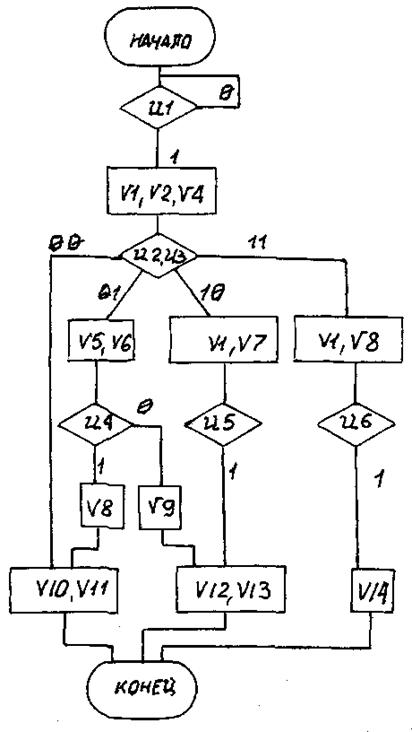
Рис. П45
Вариант 46
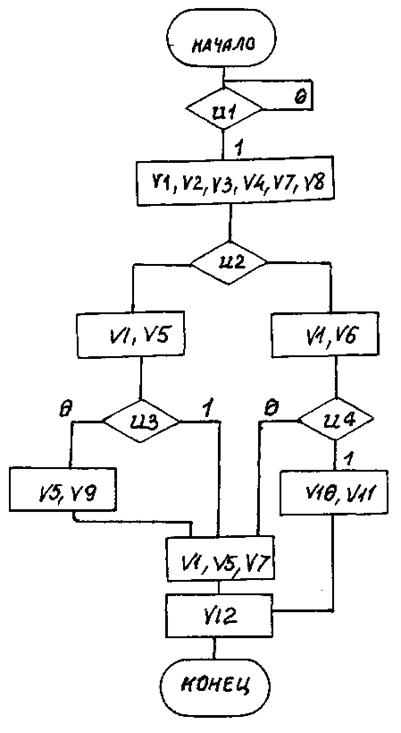
Рис. П46
Вариант 47

Рис. П47
Вариант 48

Рис. П48
Вариант 49
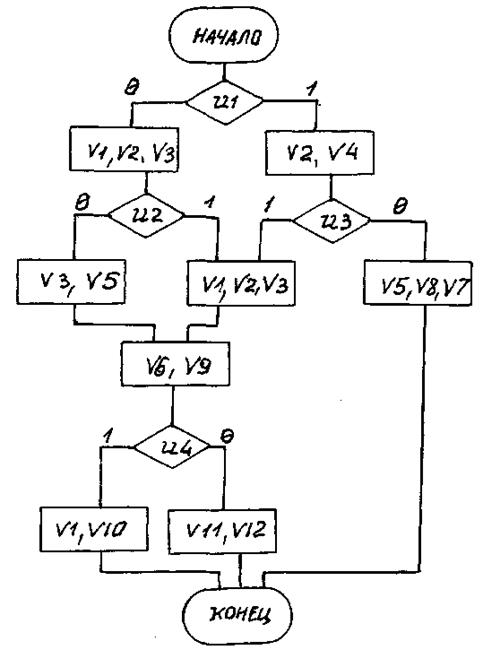
Рис. П49
Вариант 50
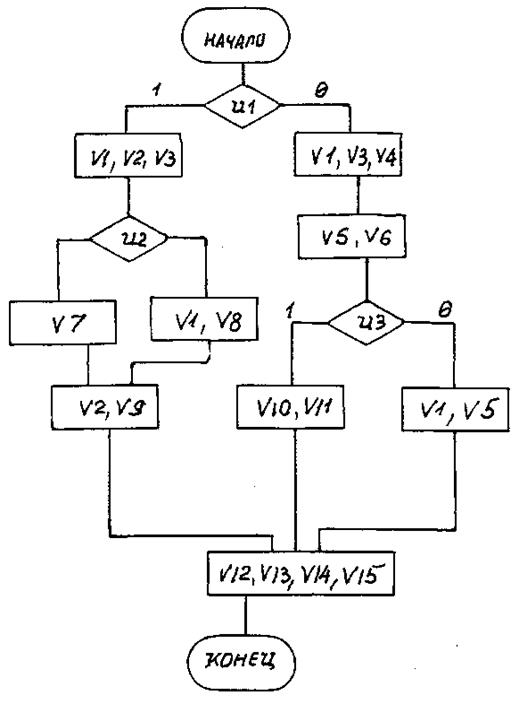
Рис. П50
