Аэродинамическая модель аппарата
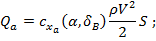
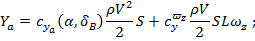
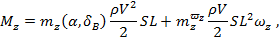
где зависимости аэродинамических коэффициентов от угла атаки α и угла отклонения рулей высоты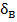 
приведены далее.
Аэродинамические коэффициенты представлены в функции «углов атаки»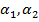 
вида
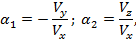
связанных с общепринятыми углами атаки и скольжения α, β соотношениями
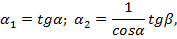
дающими при малых α, β
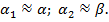
Рекомендуемые приближенные выражения для расчета позиционных аэродинамических коэффициентов, учитывающих перекрестные связи, имеют следующую структуру:
;
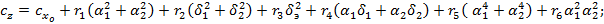
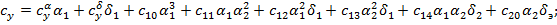
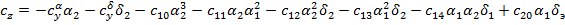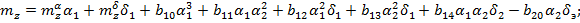
Здесь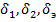 
обозначены соответственно углы отклонения рулей в канале тангажа (горизонтальные рули),в канале курса(вертикальные рули) и углы отклонения элеронов.
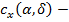коэффициент продольной составляющей аэрогидродинамической силы;
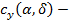коэффициент нормальной составляющей аэрогидродинамической силы;
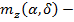коэффициент аэрогидродинамического момента;
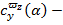коэффициент вращательной производной от нормальной составляющей аэрогидродинамической силы по безразмерный угловой скорости 
;
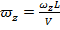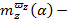коэффициент вращательной производной от аэрогидродинамического момента по безразмерной угловой скорости 
.
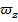Перечисленные характеристики являются функциями угла атаки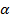 
, а некоторые из них зависят еще и от угла отклонения рулей глубины 
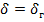(для подводной ступени) или рулей высоты 
(для воздушной ступени).
Аналогичные зависимости справедливы для плоскости Oxz аппарта:
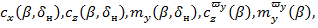где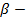 
угол скольжения, а 
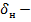угол отклонения рулей направления.
Для осесимметричных аппаратов справедливы соотношения
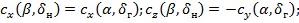
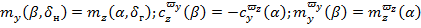
при условии
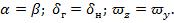
В практическом диапазоне изменения углов атаки (скольжения) коэффициенты вращательных производных принимаются постоянными, а коэффициент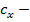 
независимым от угла атаки, но пропорциональным квадрату угла отклонения рулей. Зависимость коэффициентов 
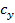и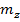 
от углов атаки 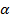рассматривается как кубическая, а от углов 
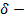как линейная.
Таким образом, для расчетов в плоскости дифферента (тангажа) будут использоваться следующие структуры представления АГДХ:
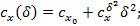
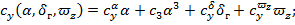
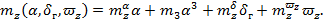
Аналогичная структура используется для коэффициентов , соответствующих плоскости Oyz,
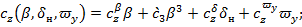
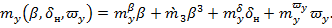
Расчет коэффициентов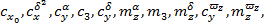 
а также
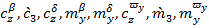производится по существующим полуэмпирическим методикам либо путем аппроксимации данных экспериментальных продувок в аэродинамической трубе или испытаний в гидроканале. В последнем случае требуется совпадение значений производных при 
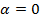и значений коэффициентов, соответствующих балансировочным углам атаки 
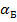, которые определяются из условия 
.
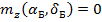При рассмотрении некоторых движений (циркуляция, разгон, торможение) существует необходимость учесть влияние числа Re (V) на коэффициент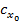 
. Для этого удобно использовать аппроксимацию в виде зависимости 
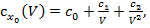где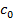 
, 
, 
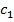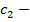постоянные величины.
Пересчет АГДХ на скоростную систему координат производится по формулам
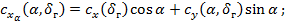
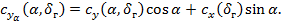
Зависимость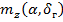 
, а также значения производных 
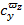и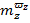 
сохраняются при переходе от связанной к скоростной системе координат. В практическом диапазоне углов атаки (скольжения) можно принять 
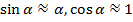, тогда зависимости принимают вид:
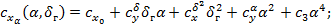
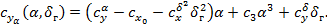
Приведенные выше зависимости, как правило, используются при проектировании подводной ступени, имеющей существенную нелинейность гидродинамических характеристик и не обладающей статической устойчивостью при малых углах атаки.
При развитых несущих поверхностях и статической устойчивости аппарата, что характерно для его воздушной ступени, можно воспользоваться упрощенной структурой представления АДХ в скоростной системе координат:
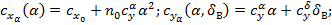
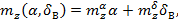
где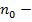 
некоторый поправочный коэффициент,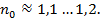 
Текст программы
% - Курсовой проект
% - Федоров Дмитрий, 06-518
%---------------------------
% - Аэродинамическая модель (для КАБ)
% - Литература: "Динамика систем наведения управляемых авиабомб"
% Э.Я.Соловей, А.В.Храпов
clc
% - Необходимые начальные данные: -----------------------------------------
H=1000; % - начальная высота
Vs=100; % - скорость самолета
m=300; % - масса аппарата
dt=0.1; % - шаг
kks=1; % - № конструктивно компановочной схемы
% - Углы: -----------------------------------------------------------------
tets=0; % - угол наклона траектории самолета
tet=tets;
psi=0;
alph=0;
gam=0;
fi=0;
% - Конструктивно компановочная схема: ------------------------------------
switch (kks)
case 1
% -- 1 -- "Бесхвостка (а)" --------------------------------------------
value=[20, 0.75, 0.4, 3.05, 3.99, 0.123, 0.23, 23, 23, 1.5, 2.7, 2.1, 1.9];
case 2
% -- 2 -- "Бесхвостка (б)" --------------------------------------------
value=[20, 0.75, 0.35, 3.05, 5.35, 0.12, 0.26, 30, 30, 2.0, 3.9, 2.4, 2.2];
case 3
% -- 3 -- "Бесхвостка (в)" --------------------------------------------
value=[20, 1.3, 0.58, 4.63, 5.83, 0.15, 0.34, 26, 24, 1.7, 2.8, 2.4, 2.1];
case 4
% -- 4 -- "Утка" ------------------------------------------------------
value=[5, 1.1, 0.3, 2.75, 9, 0.2, 0.73, 6, 5, 1.8, 2.6, 3.5, 3.2];
case 5
% -- 5 -- "Нормальная (а)" --------------------------------------------
value=[20, 0.75, 0.35, 2.6, 10.24, 0.19, 0.42, 30, 28, 4.7, 7.3, 3.0, 2.4];
case 6
% -- 6 -- "Нормальная (б)" --------------------------------------------
value=[20, 1.56, 0.4, 4.96, 25, 0.27, 1.05, 29, 29, 3.0, 5.2, 4.5, 4.2];
end
% -------------------------------------------------------------------------
sigm_max=value(1); % [град]
lmax=value(2); % [м] - максимальный размах основных несущих поверхностей
d=value(3); % [м] - диаметр корпуса
L=value(4); % [м] - длина аппарата
Snp_S=value(5); % Snp - суммарная площадь несущих поверхностей
Snp_Som=value(6); % S - площадь миделя
U=value(7);
alph_pbal_06=value(8); % [град] - балансировачные значения пространственного
alph_pbal_08=value(9); % [град] угла атаки
ny_max_06=value(10); %
ny_max_08=value(11); %
Kmax_06=value(12);
Kmax_08=value(13);
% - Назначение начальных данных: ------------------------------------------
Vgc=0; % !!!!!!!!!!!
S=(pi*d^2)/4;
Snp=Snp_S*S;
g=9.8;
V0=Vs;
tet0=tet;
Xg0=0;
Yg0=Vgc;
[T, a, P, rho] = atmosisa(H);
M0=V0/a;
Cx0=0.22;
Cy0=0.1;
Cx_alph=0.00053^2;
Cy_alph=0.046;
X0=0; % начальная координата X
Y0=H; % начальная координата Y
Z0=0; % начальная координата Z
t0=0; % [сек]
% - Упрощенная аэродинамическая модель: -----------------------------------
i=0;
best=[0,0,0];
for alph=[5:1:30]
i=i+1;
Cx=Cx0+Cx_alph*(alph^2);
Cy=Cy_alph*alph;
V=V0;
t=t0;
X=X0;
Y=Y0;
Z=Z0;
while (Y>0)
[T, a, P, rho] = atmosisa(Y);
q=(rho*V^2);
Xa=Cx*q*Snp;
Ya=Cy*q*Snp;
dV_dt=-Xa/m-g*sin(tet);
dtet_dt=(Ya*cos(gam)/(m*V))-(g*cos(tet))/V;
dpsi_dt=(Ya*sin(gam))/((m*V)*(-cos(tet)));
dX=V*cos(tet)*cos(psi);
dY=V*sin(tet);
dZ=-V*cos(tet)*sin(psi);
V=V+dV_dt*dt;
tet=tet+dtet_dt*dt;
psi=psi+dpsi_dt*dt;
X=X+dX*dt;
Y=Y+dY*dt;
Z=Z+dZ*dt;
t=t+dt;
end
disp(['- Результат расчета по упрощенной модели(при alph=',num2str(alph),'):'])
disp([' Время полета = ',num2str(t),'[сек]'])
disp([' Точка приземления = (X=',num2str(X),', Y=',num2str(Y),', Z=',num2str(Z),')'])
if (X>best(1))
best(1)=X;
best(2)=t;
best(3)=i;
end
end
clc
disp(' ')
disp(' В результате предварительных расчетов было установлено, что при выбранной')
disp(['компановочной схеме (№',num2str(kks),'), наибольшая дальность достигаемая'])
disp(['аппаратом = ',num2str(best(1)),', при условии alph=',num2str((best(3)-1)*1),', время полета составит ',num2str(best(2)),' сек '])
% - Блок расчета аэродинамических сил и моментов: -------------------------
[T, a, P, rho] = atmosisa(H);
V=V0;
t=t0;
X=X0;
Y=Y0;
Z=Z0;
tet=tet0;
omeg_x=0;
omeg_y=0;
omeg_z=0;
Cz=0;
dCx=0;
dCy=0;
dCz=0;
Cy_int=0;
Cz_int=0;
mx=0;
my=0;
mz=0;
dmx=0;
dmy=0;
dmz=0;
mx_int=0;
my_int=0;
mz_int=0;
q=(rho*V^2);
X=-(Cx+dCx)*q*S;
Y=(Cy+dCy+Cy_int)*q*S;
Z=(Cz+dCz+Cz_int)*q*S;
M_x=(mx+dmx+mx_int+(mx^omeg_x)*L*omeg_x/V)*q*S*L;
M_y=(my+dmy+mx_int+(my^omeg_y)*L*omeg_y/V)*q*S*L;
M_z=(mz+dmz+mx_int+(mz^omeg_z)*L*omeg_z/V)*q*S*L;
% - Полная аэродинамическая модель: ---------------------------------------
tet=tets;
V=Vs;
Xg0=0;
Yg0=Vgc;
%{
V=-((cxa*q*S/m)+g*sin(tet));
tet=-g*(cos(tet))/V;
Xg=V*cos(tet)+Wgx(Yg0); % Wgx(Yg0) - составляющая ветра
Yg=V*sin(tet);
Zg=Wgz(Yg0); % Wgz(Yg0) - составляющая ветра
%}