Автоматные отображе- ния. Теорема Клини

Задавать таблицами соответствия «вход -

выход» автоматные отображения чаще

всего нельзя, так как обычно мы имеем дело с последовательностями бесконеч- ной длины. Удобной формой задания автоматных отображений является за- дание с помощью событий.

Пусть X = (X₀ , X₁ , ... X_N-1) алфавит, а
Е - множество всех слов в этом авфави- те. Любое подмножество E_j Í E называ-

ется событие в алфавите Х. Событием, представленным в автомате выходным сигналом Y_j , называется множество всех слов из Е, отображения на которые, индуцируемые автоматом, оканчивают-

ся Y_j .

Алгебра событий в алфавите Х - это множество всех событий в этом ал-

фавите, на котором заданы операции дизъюнкции, произведения и итера-

ции.

Дизъюнкция событий R Ú Q - это собы- тие , состоящее в объединении событий

R и Q.

Пример

R = (X₀ , X₁X₀ )

Q = (X₁ , X₁X₀X₁)

R Ú Q = (X₀ , X₁X₀ , X₁ , X₁X₀X₁)

Произведение событий R×Q - это собы- тие, состоящее из всех слов вида r×q, где rÎR а qÎQ. (К любому слову из R спра-

ва приписывается любое слово из Q). Произведение некоммутативно: R×Q ¹

¹ Q×R.

Пример

R = (X₀ , X₁X₀ )

Q = (X₁ , X₀X₁)

R×Q=(X₀X₁, X₀X₀X₁, X₁X₀X₁, X₁X₀X₀X₁)

Q×R=(X₁X₀, X₀X₁X₀, X₁X₁X₀, X₀X₁X₁X₀)

Итерация события {R} - это событие, состоящее в объединении событий
e Ú R Ú R×R Ú R×R×R Ú ... и т.д. до бес- конечности. (е - пустое слово)

Пример

R = (X₀ , X₁X₀ )

{R} = (e, X₀ , X₁X₀, X₀X₀, X₀X₁X₀, X₁X₀X₁X₀, , X₁X₀X₀, X₀X₀X₀, ...)

В алгебре событий выделим регулярныевыражения:

1. X₀ , X₁ , ... X_N-1 и е -регулярные выражения.

2. Если R и Q - регулярные выражения, то R Ú Q, R× Q и {R} тоже регулярные выражения.

Регулярно выражение из Х (и только такое), ко-торое получается конечным числом правил 1 и 2.

Для указания порядка выполнения опе- раций в алгебре событий используются скобки ().

Одно и то же событие может выражать-

ся разными формулами. Например,
R = X₀X₁ Ú X₀X₂ Ú X₁X₀ Ú X₁X₂
можно представить как
R = X₀(X₁ Ú X₂) Ú X₁(X₀ Ú X₂)

Регулярные выражения можно преобра- зовывать, используя свойства операций, вытекающие из их определения. Например:

RÚQ = QÚR R×{R} = {R}×R

RÚ{R} = {R} {{R}} = {R}

RÚe=R PRÚPQ =Р×(RÚQ)

R×e = e×R = R PQÚRQ = (PÚR)×Q

Те события, для которых существуют регулярные выражения, называются регулярными событиями.

Рассмотрим примеры регулярных событий в алфавите X = (X₀, X₁, X₂).

1. Универсальное событие:
R = { X₀ Ú X₁ Ú X₂ }

2. Событие из всех двухбуквенных слов:
R = (X₀ Ú X₁ Ú X₂)×(X₀ Ú X₁ Ú X₂)

3. Событие из всех слов, заканчивающихся на X₀X₂X₁ :
R = { X₀ Ú X₁ Ú X₂ } ×X₀ ×X₂ ×X₁

4. Событие из всех слов четной длины:
R = { (X₀ Ú X₁ Ú X₂)×(X₀ Ú X₁ Ú X₂)}

5. . . .
R = { X₀ Ú X₁ } ×X₂ ×X₂

События могут быть нерегулярными (естественно, при бесконечной длине).

Покажем это на примере события Т из всех слов алфавита Х длиной n₁,n₂, ... ,

n_i, ... при i = 1,2, ... i, ... где n_i = (i)².

Пусть Т имеет регулярное выражение. Так как Т бесконечное событие, то его выражение содержит итерацию. Найдем внешнюю итерацию, не входящую в другие. Тогда Т может иметь вид Т =

= Р×{T₁}×QÚ... , где P и Q - любые регу- лярные выражения.

Отсюда следует, что в Т входят слова, образованные из P×Q,P×T₁×Q,P×T₁×T₁×Q,...

Длины этих слов образуют арифмети- ческую прогрессию, а числа n₁,n₂, ... ,n_i,

... при n_i = (i)² - не образуют.

\Т - нерегулярное событие.

Что касается регулярных событий, то теорема доказанная Клини утверждает:

класс событий, представимых в ко-

нечных автоматах, совпадает с клас-

сом регулярных событий.

Любое регулярное событие может быть представлено автоматом Мура. Автомат, представляющий событие E_i , распозна-

ет входную последовательность и пере- ходит в состояние, отмеченное y_i , если последний символ входной последова- тельности завершает цепочку символов, образующих слово из E_i .

Каждое состояние автомата должно идентифицировать входные последо- вательности, приводящие в него так, чтобы была возможность однозначно продолжать распознавание входной последовательности как начальной

части слов из E_i .

Если входная последовательность не является словом из E_i , то она может являться начальной частью одного или нескольких слов из E_i .

Пример

E_i = (X₁X₂X₀, {X₀}X₁X₂X₁, ... )

Входная последовательность X₁X₂ мо- жет быть началом 2-х слов из E_i .

Теорема Клини определяет возможнос-

ти автоматов, ограничивая их отобра- жениями конечной длины, либо беско- нечными, включающими фиксирован- ные последовательности конечной дли- ны или периодически повторяющиеся.

Структурные автоматы. Общие положения.

Композиции автоматов.

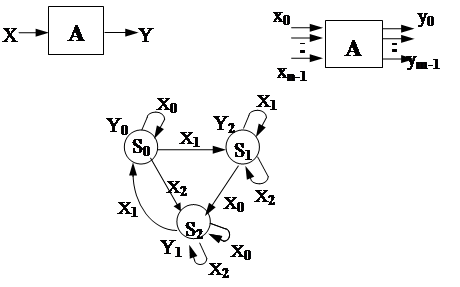
Моделью абстрактного автомата явля-

ется объект с 1 входом и 1 выходом.

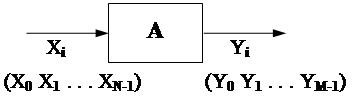Ни вид сигналов, ни внутренняя струк- тура абстрактного автомата не рассмат- риваются.

В структурной теории автоматов обьек- том изучения являются так называемые структурные автоматы и их композиции.

Структурный автомат - это объект, име- ющий совокупность входных и выход- ных каналов (входов и выходов), по ко- торым передаются элементарные сигна- лы, представляющие перерабатываемые автоматом символы.

y0

.

.

ym-1

xn-1

.

.

.

.

x0

А

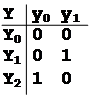
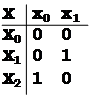
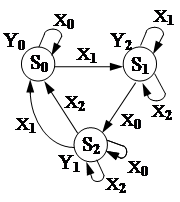
Элементарные сигналы отображают структурный алфавит автомата. В нас- тоящее время это чаще всего двоичный алфавит.

Наборы символов структурного алфа- вита однозначно задают (кодируют) символы алфавитов абстрактного автомата.

Кодируя символы абстрактного автома- та, можно перейти от описания поведе- ния абстрактного автомата к описанию структурного. (Возможен и обратный переход.)

В примере структурный алфавит

для всех символов двоичный:

x₀ = (0;1) , x₁ = (0;1)

y₀ = (0;1) , y₁ = (0;1)

Композиция структурных автоматов

состоит в том, что для совокупности

автоматов производится отождествле-

ние (соединение) входов и выходов

отдельных автоматов. Некоторые вхо-

ды и выходы при этом отмечаются как

внешние.

Автоматы, образующие композицию, работают в некоторой системе тактнос- ти.

Выделение тактов и пауз между ними
на полуоси времени означает разбиение времени на периоды.

Период такта - время от начала i-го до начала (i+1) -го такта (i-ый период).

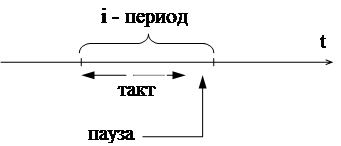В структурной теории авиоматов поня-

тие такта детализируется, т.к. в ней, в

частности, рассматривается задача пос-

троения физических моделей автоматов

и способы интерпретации систем

тактности.

Для автомата существует интервал

времени в периоде t, когда значения

X неизменны и в соответствии с

функциями выходов и переходов оп-

ределяют значения Y и S. Это время

будем называть

входным микротактом t¹.

Интервал времени в периоде t, когда

значения Y неизменны и соответствуют значениям функции выходов, будем на-

зывать выходным микротактом t⁰.

В композиции автоматов соединение

выхода автомата A_i со входом автомата

A_j возможно только в случае, если 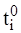со-

вместим с 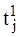, то-есть, если любой момент времени из 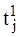принадлежит .

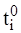Наиболее употребимы следующие

варианты организации тактности:

1.Композиции автоматов с единой (общей для всех автоматов) системой такт-ности.

Для такой композиции существует единое (общее) разбиение полуоси времени на периоды тактов для всех автоматов композиции.

2. Композиции автоматов с различными системами тактов.

В таких композициях автоматы

могут быть разбиты на под-

множества авто матов, в каждом

из которых использу ется своя

единая система тактности.

При этом можно выделить два основ-

ных вида композиций:

а) композиции с несопрягаемыми системами тактов;

б) композиции с сопрягаемыми системами тактов;