Метод статистического моделирования
Для начала введем в рассмотрение логическую структурную функцию сети F(x), где логический вектор х=(х1,х2,...,хn) характеризует работоспособность элементов сети (здесь n равно количеству элементов сети или сумме общего числа ребер и узлов в графе). Пусть хi=1 означает, что i-й элемент работоспособен, а хi=0 - i-й элемент отказал. Функция F(x) выбрана так, что равна единице, когда сеть работоспособна. Следует отметить, что сеть считается неработоспособной, если отказала связь между какой либо парой узлов.
Идея метода статистического моделирования заключается в генерировании логических переменных хi с заданной вероятностью pi возникновения единицы:
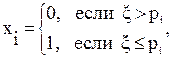 (3)
(3)
где 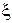 - случайная величина, равномерно распределенная в интервале [0,1]. Такие логические переменные подставляются в логическую структурную функцию моделируемой сети. Процесс вычисления повторяется N0 раз, при этом подсчитывается количество N единичных значений функции. Отношение N/N0 является статистической оценкой Pc вероятности безотказной работы.
- случайная величина, равномерно распределенная в интервале [0,1]. Такие логические переменные подставляются в логическую структурную функцию моделируемой сети. Процесс вычисления повторяется N0 раз, при этом подсчитывается количество N единичных значений функции. Отношение N/N0 является статистической оценкой Pc вероятности безотказной работы.
Величина N0 определяет точность получаемого значения Pc: чем больше число испытаний N0, тем меньше погрешность вычислений. Погрешность получаемого значения величины Pc определяется следующим образом:
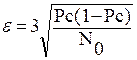 . (4)
. (4)
Из формулы (4) видно, что для увеличения точности результата на порядок необходимо увеличить количество испытаний на два порядка.
 Основной недостаток метода заключается в необходимости nN0 кратного генерирования случайной величины
Основной недостаток метода заключается в необходимости nN0 кратного генерирования случайной величины 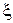 , т.е. в увеличении объема испытаний при повышении требуемой точности результата.
, т.е. в увеличении объема испытаний при повышении требуемой точности результата.
Пример 1
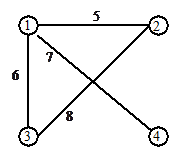
Рассмотрим сеть, заданную графом на рис. 19.
 Пусть наработка на отказ равна T1=100000 ч. (для узлов) и T2=50000 ч. (для ребер), а рассматриваемый период времени равен t=10000 ч.
Пусть наработка на отказ равна T1=100000 ч. (для узлов) и T2=50000 ч. (для ребер), а рассматриваемый период времени равен t=10000 ч.
Тогда вероятность безотказной работы для каждого узла и ребра графа будет соответственно равна:
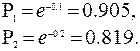
Выделим в графе все пути между всеми парами вершин (табл. 3) и составим логическую структурную функцию сети:
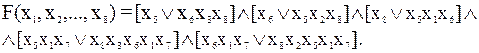
 В табл. 3 в столбце «пути» указаны через запятую все возможные пути перехода из i-й вершины в j-ю. Каждый путь состоит из номера транзитного узла (выделено жирным шрифтом) и стоимости линии связи.
В табл. 3 в столбце «пути» указаны через запятую все возможные пути перехода из i-й вершины в j-ю. Каждый путь состоит из номера транзитного узла (выделено жирным шрифтом) и стоимости линии связи.
Данная функция принимает значение, равное 1, когда нет нарушения связи между какой-либо парой узлов. В противном случае она принимает значение, равное 0.
Примем количество испытаний равное N0=10000, тогда нам необходимо генерировать случайную величину 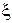 - 80000 раз.
- 80000 раз.
В результате моделирования получиливероность безотказной работы сети равную, Pc=0.6649.Погрешность полученного результата будет равна: