Методы наименьших квадратов Форсайта

Рассмотренные методы позволяют аппроксимировать функции, заданные экспериментальными данными, с помощью интерполяционных многочленов. На практике интерполяционные формулы применяются в тех случаях, когда ошибки в данных можно не учитывать и число N точек Xj является малым. При больших N эти формулы становятся громозкими, а также возникают трудности, связанные с неустойчивостью интерполяционного процесса отрезка [a,b].

В реальных задачах ошибки в экспериментальных данных необходимо учитывать. Если зависимости между параметрами являются достаточно гладкими, то даже при больших N часто нет необходимости выбирать для аппроксимации полиномы, имеющие высокую степень n. В этом случае при аппроксимации функций можно использовать метод наименьших квадратов (МНК).

Предположим, что функция Y=f(X) задана на отрезке [a,b] экспериментальными значениями:

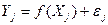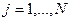, , (2.12)

где

ej - некоррелированные случайные величины, имеющие

нулевое математическое ожидание и дисперсию s² . При аппроксимации функции Y=f(X) алгебраическим полиномом (2.12) с помощью МНК, по экспериментальным данным необходимо оценить коэффициенты a_k полинома таким образом, чтобы сумма квадратов была минимальной

N

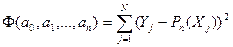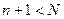, , (2.13)

Алгебраический полином (2.12) является частным случаем общей линейной модели

,

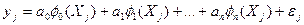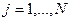
Оценивание коэффициентов общей линейной модели сводится к решению

системы нормальных уравнений 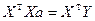, которая для приближения (2.12) имеет вид:

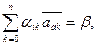
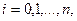(2.14)

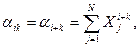
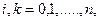(2.15)

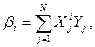
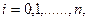(2.16)

где

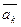- оценки коэффициентов .

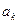Решение системы (2.14)существует если определитель D_n+1 ¹ 0

Однако при практической реализации МНК на ЭВМ может оказаться, что определитель D_n+1 системы (2.14) даже при сравнительно малых n близок к нулю, что может привести к грубым ошибкам при решении задач.

Анализ кривых

3.1 Кривая n=3

Так выгладят исходные данные для кри вой n=3

X	Y(X)
	0,28
	0,3
	0,36
	0,47
	0,57
	0,68
	0,72
	0,74
	0,75

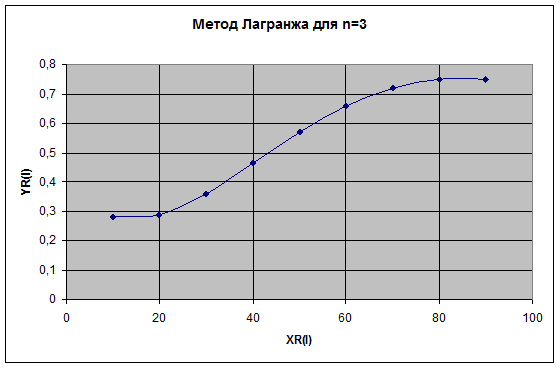
3.1.1 Алгебраический полином Лагранжа для n=3

№	XR(I)	YR(I)
		0,28
		0,286797
		0,36
		0,463672
		0,57
		0,659297
		0,72
		0,748672
		0,75

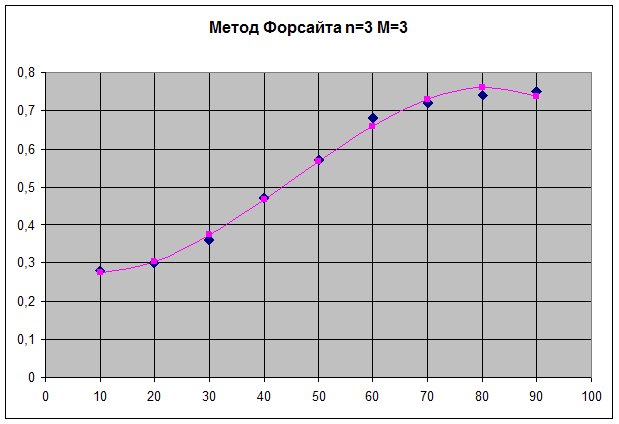
Метод наименьших квадратов Форсайта

Для n=3 M=3

№	X(I)	Y(I)	YR(I)
		0,28	0,2741
		0,3	0,3041
		0,36	0,3732
		0,47	0,4657
		0,57	0,5661
		0,68	0,6591
		0,72	0,7291
		0,74	0,7606
		0,75	0,738

Коэффициенты полинома:

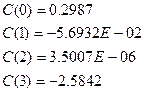
Остаточная дисперсия:

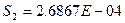
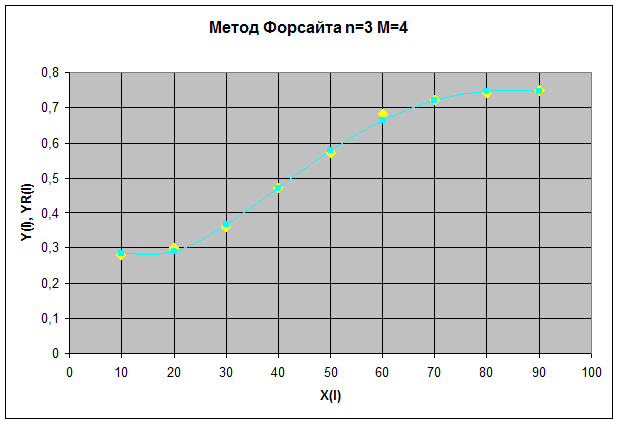
Для n=3 M=4

№	X(I)	Y(I)	YR(I)
		0,28	0,2833
		0,3	0,2904
		0,36	0,366
		0,47	0,4715
		0,57	0,578
		0,68	0,665
		0,72	0,7219
		0,74	0,7468
		0,75	0,7471

Коэффициенты полинома:

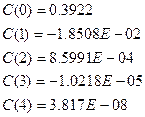
Остаточная дисперсия:

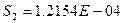
Для n=3 M=5

№	X(I)	Y(I)	YR(I)
		0,28	0,2801
		0,3	0,2991
		0,36	0,3628
		0,47	0,4644
		0,57	0,5779
		0,68	0,6721
		0,72	0,7251
		0,74	0,7381
		0,75	0,7503

Коэффициенты полинома:

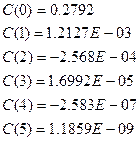
Остаточная дисперсия:

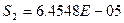
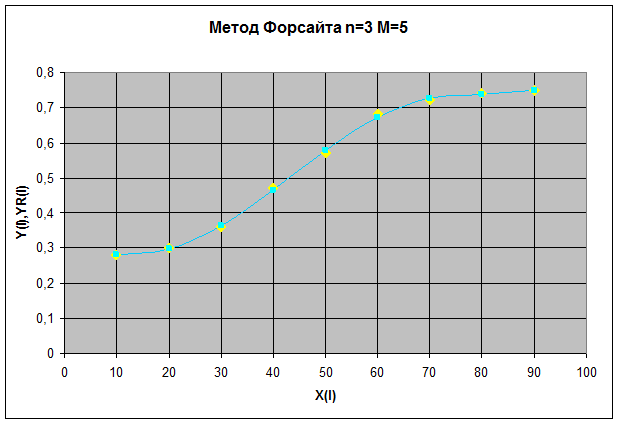
3.1.3 Интерполяционный полином Ньютона для n=3

№	XR(I)	YR(I)
		0,28
		0,286797
		0,36
		0,463672
		0,570001
		0,659299
		0,720004
		0,748679
		0,750012

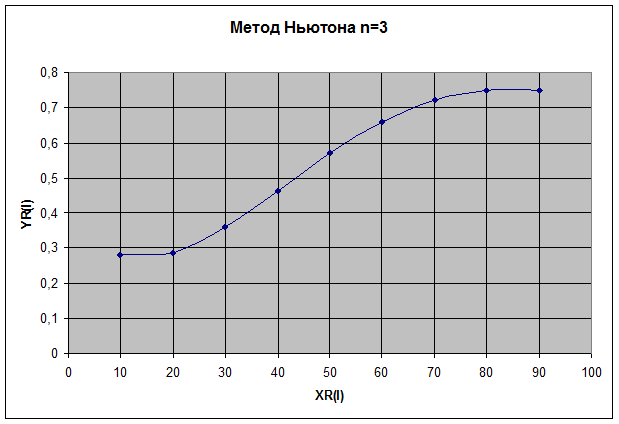
3.2 Кривая n=6

Исходные данные для кривой n=6:

X	Y(X)
	0,08
	0,09
	0,12
	0,18
	0,22
	0,29
	0,31
	0,33
	0,36

3.2.1 Алгебраический полином Лагранжа для n=6

№	XR(I)	YR(I)
		0,08
		0,0866
		0,12
		0,1678
		0,22
		0,2691
		0,31
		0,3403
		0,36

Метод наименьших квадратов Форсайта

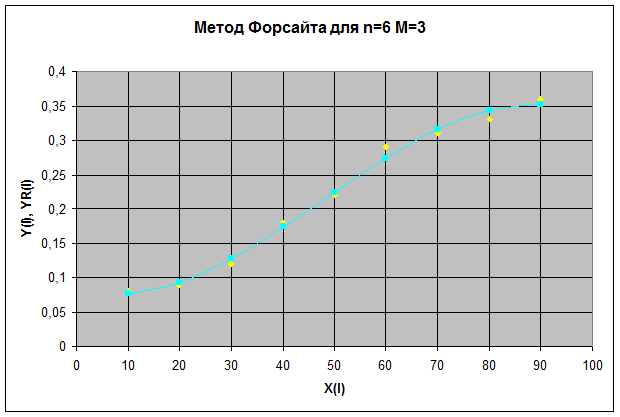
Для n=6 М=3

№	X(I)	Y(I)	YR(I)
		0,08	0,0762
		0,09	0,0934
		0,12	0,128
		0,18	0,1736
		0,22	0,2241
		0,29	0,2734
		0,31	0,3153
		0,33	0,3437
		0,36	0,3523

Остаточная дисперсия:

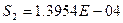
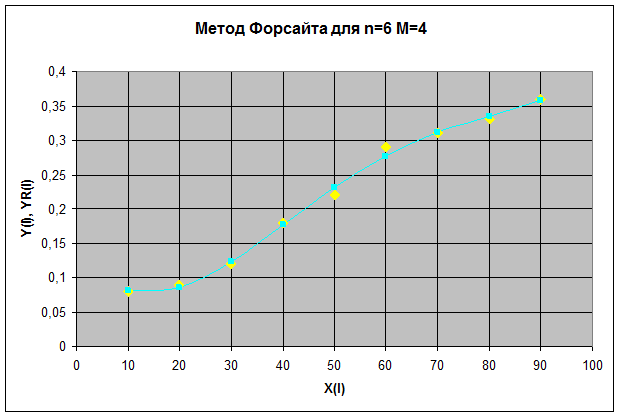
Для n=6 М=4

№	X(I)	Y(I)	YR(I)
		0,08	0,0818
		0,09	0,085
		0,12	0,1236
		0,18	0,1772
		0,22	0,2313
		0,29	0,277
		0,31	0,3109
		0,33	0,3353
		0,36	0,3579

Остаточная диспер сия:

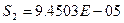
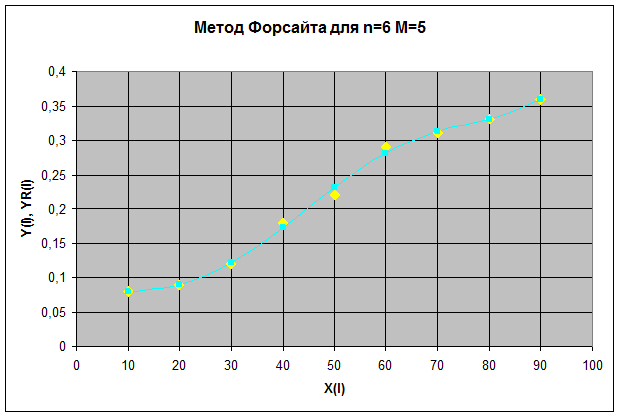
Для n=6 М=5

№	X(I)	Y(I)	YR(I)
		0,08	0,0798
		0,09	0,0905
		0,12	0,1216
		0,18	0,1728
		0,22	0,2313
		0,29	0,2814
		0,31	0,3129
		0,33	0,3299
		0,36	0,3599

Остаточн ая дисперсия:

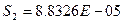
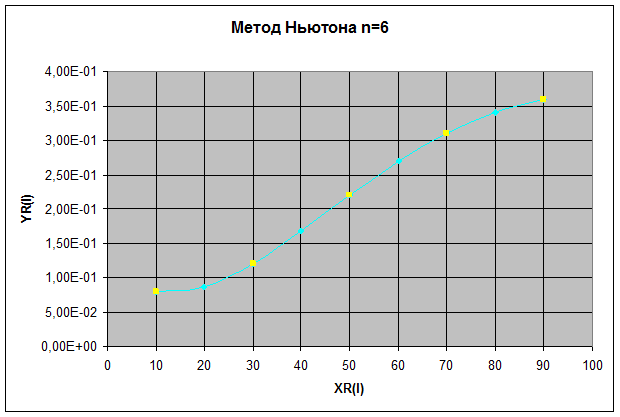
3.2.3 Интерполяционный полином Ньютона для n=6

№	XR(I)	YR(I)
		8,00E-02
		8,66E-02
		0,12
		0,1678
		0,22
		0,2691
		0,310001
		0,3403
		0,360004