Вычисление функций двух переменных

Примерами объектов подобного вида второго порядка являются эллипсоид, гиперболоид, параболоид, конус второго порядка и многие другие. Рассмотрим построение эллипсоида, под которым понимается поверхность, определяемая в системе декартовых прямоугольных координат следующим уравнением:

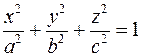(2.1)

Такое уравнение описывает эллипсоид, представляющий собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии.

Для построения эллипсоида в Excel каноническое уравнение (2.1) необходимо решить относительно переменной z(представить в виде функции z=f(x, у):

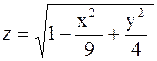
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х=[–3; 3], у=[–2; 2] с шагом ∆х =0,5 для обеих переменных. Введем значения переменной хв столбец А,для чего в ячейку А1 вводим символ х, а в ячейку А2 вводится первое значение аргумента (–3). В ячейку A3 вводится второе значение аргумента - левая граница диапазона плюс шаг построения (–2,5).Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).

Значения переменной увводим в строку 1, для чего в ячейку В1 вводится первое значение переменной у= -2. В ячейку С1 вводится второе значение переменной у=-1,5 в соответствии с заданным шагом переменной у. Затем, выделив блок ячеек В1:С1, автозаполнением вводим все остальные значения аргумента у (за правый нижний угол блока протягиваем до ячейки J1).

Далее вводим значения функции z в соответствии с уравнением (4.1). Для этого табличный курсор необходимо поместить в ячейку В2 и на панели инструментов Стандартная нажать кнопку Вставка > Функции f_x. В появившемся диалоговом окне Мастер функций шаг 1 из 2 в поле Категория выбираем Математические. Справа в поле Функция выбираем функцию Корень,нажимаем кнопку ОК и появляется диалоговое окно Корень. В рабочее поле вводим подкоренное выражение: 1- $А2^2/9-В$1^2/4, обратите внимание, что символы $ предназначены для фиксации адреса столбца А - переменной х истроки 1 - переменной у. Нажимаем кнопку ОК. В ячейке В2 появляется #ЧИСЛО! (при х=–3 и у=–2 точек рассматриваемого эллипсоида не существует). Теперь необходимо скопировать функцию из ячейки В2, для чего автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего (протягиванием вниз) - в диапазон ВЗ:J14. В результате должна быть получена следующая таблица точек эллипсоида.

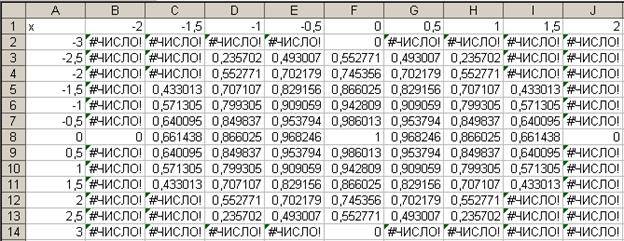
Рис.2.40. Вычисление функции Z

Для построения диаграммы на панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы - Поверхность, и вид - Проволочная (прозрачная) поверхность, после чего нажимаем кнопку Далее в диалоговом окне.

В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных B2:J14.

Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах. Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей, для чего щелкните в нем указателем мыши и введите диапазон подписей оси х-А2: A14.

Вводим значения подписей оси у, для чего в рабочем поле Ряд указываем первую запись Ряд 1 и в рабочее поле Имя, активизировав его указателем мыши, вводим первое значение переменной у: -2. Затем в поле Ряд указываем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: –1,5. Повторяем таким образом до последней записи - Ряд 9 и после появления требуемых записей нажимаем кнопку Далее.

В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Эллипсоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z. Далее следует нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграммаэллипсоида (рис.2.41).

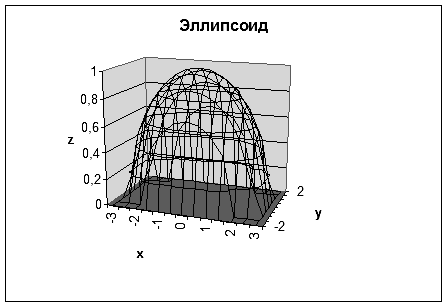
Рис.2.41. Построение эллипсоида

2.8.5. Решение нелинейного уравнения

Решение уравнений средствами Excel является одним из полезных прикладных применений для инженерных задач. Пусть задано следующее квадратное уравнение: 2х² + 3х – 9 = 0, для определения корней которого необходимо выполнить следующее. Решение уравнения будем формировать в одной из ячеек листа Excel, например в В1, в которую введем искомое значение корня х=0. Исходное уравнение запишем в виде формулы в ячейку В2 (рис.2.42). Для получения решения уравнения вызовем средство Excel Подбор параметра, которое является частью блока задач, иногда называемым инструментом анализа«что-если». Под данным анализом понимают процесс изменения значений ячеек и последующий анализ влияния данных изменений на результат вычисления формулы.

Вызов средства Подбор параметра осуществляется из меню Сервис (рис.2.42).

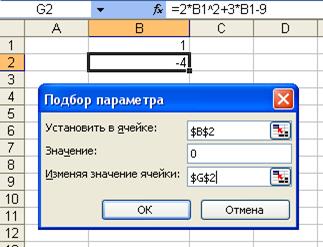
Рис.2.42. Окно Подбор параметра

Для подбора определяемого параметра Excel в одной конкретной ячейке изменяет значение (в нашем примере это ячейка В1) до тех пор, пока формула, зависимая от этой ячейки, не возвращает требуемый результат, то есть 0 для рассматриваемого примера (рис.2.43).

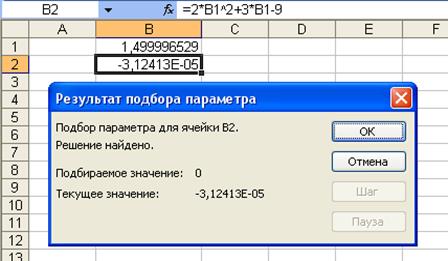
Рис.2.43. Решение уравнения методом подбора результата

В результате решения уравнения Excel сформировал вместо точного результата х=1,5 приближенный результат х=1,499996529, что связано с использованием интерактивных приближенных методов вычислительной математики, полученная погрешность <0,00001. В качестве начального значения в ячейке В1 можно ввести и другое, например 0. Попробуйте самостоятельно рассмотреть и другие варианты.

2.8.6. Решение системы уравнений

Рассмотрим в качестве примера решение системы нелинейных уравнений с двумя неизвестными в ограниченных пределах изменения переменной Х, что часто требуется в экономических задачах:

У=Х² +2;

Z=3/Х +2.

Решением системы уравнений будет являться точка пересечения двух функций У=F(X) и Z=F(X), а точность определяется выбранным шагом дискретизации переменной Х, переменная Х задана в интервале Х=(0,1-2) с шагом ∆Х=0,1 (рис.2.44).

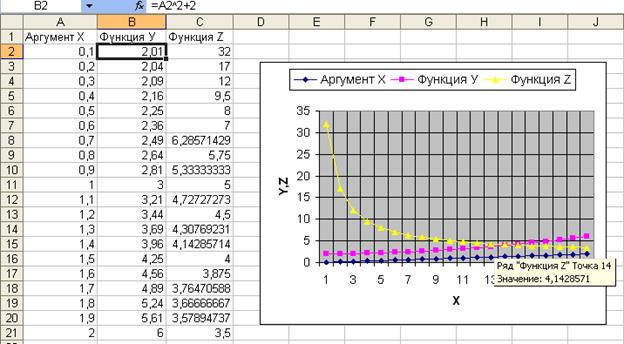
Рис.2.44. Решение системы уравнений

Для построения данных функций в столбце А заданы значения переменной Х, в ячейках В2:В21введены формулы для вычисления функции У= Х² +2, а в ячейках С2:С21 - формулы для вычисления функции Z=3/Х +2. Решением системы уравнений является значение Х= 1,44 на пересечении графиков функций У и Z. Как видно из графиков, более точное решение можно получить при использовании шага ∆Х=0,05.

2.8.7. Численное интегрирование функций

Вначале остановимся кратко на понятии определенный интеграл. Пусть на отрезке [a, b] задана функция y =f(х), и отрезок [a, b] разбит на n элементарных отрезков в точках х₀., х₁,..., х_n.: а = х₀<х₁<х₂<...<х_п = b.

На каждом отрезке разбиения [x_i-1., x_i] выбрана некоторая точка ζ_i и положено, что ∆x_i = x_i - x_i-1, где i = 1, 2, ..., п. Тогда сумму вида:

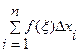
называют интегральной суммой функции y =f(х) на [a, b]. Данная интегральная сумма определяется как способом разбиения отрезка [a, b], так и выбором точек ζ₁, ζ₂,... ζ_n = 0 на каждом из отрезков разбиения ∆x_i = x_i – x_i-1, i = 1, 2, ..., n. Обозначим через max ∆x_i максимальную из длин отрезков [x_i-1, x_i], где i = 1, 2, ..., n.

Тогда определенным интегралом от функции y =f(х) на [a, b] называют предел интегральной суммы при стремлении max x_i, к нулю, если он существует, конечен и не зависит от способа выбора точек х₁, х₂,. и точек ζ₁ ζ₂. Определенный интеграл обозначается как:

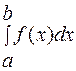
а f(x) называют интегрируемой в пределах [a, b], то есть:

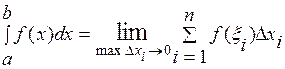
Число а называют нижним пределом определенного интеграла, число b - его верхним пределом.

Геометрический смысл определенного интеграла заключается в следующем. Если функция y =f(х) неотрицательна на отрезке [a, b], где а < b, то 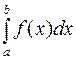численно равен площади S под кривой у =f(x) на [a, b] .

Действительно, отдельное слагаемое интегральной суммы (1) равно площади S_i прямоугольника со сторонами ∆x_i и f(x.) (согласно определению значение определенного интеграла не зависит от способа выбора точек ζ₁, ζ₂,...), где i= 1, 2,... n (рис. 4.45). Поэтому вся интегральная сумма (1) равна площади S_i = S_i+S₂+...+S_n под ломаной, образованной на каждом из отрезков [x_i-1, x_i] прямыми, параллельными оси абсцисс. При стремлении max ∆x_i к нулю ломаная неограниченно приближается к исходной кривой, а площадь под ломаной переходит в площадь под кривой S_i = S.

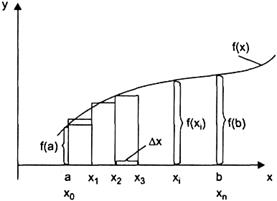
Рис. 2.45. Графическая интерпретация определенного интеграла

В экономических приложениях определенный интеграл может выражать, например, объем произведенной продукции (и) при известной функции производительности труда f(t):

.

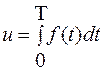Обычно для нахождения определенного интеграла используется формула Ньютона-Лейбница:

.

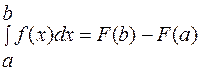Однако применение формулы (3) на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае усложнения подынтегральной функции. Поэтому в приложениях используют так называемые численные методы, позволяющие найти приближенное значение искомого интеграла с требуемой точностью. Этот подход оказывается особенно предпочтительным при использовании компьютеров для нахождения интегралов.

Существует значительное количество численных методов вычисления интегралов. Они основаны на разных способах нахождения площади под кривой f(х):

как суммы элементарных трапеций - метод трапеций:

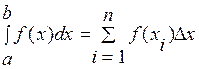
,как суммы элементарных прямоугольников - метод прямоугольников:

.

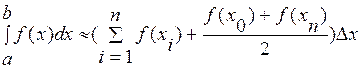Существуют также метод Симпсона и ряд других.

Формула метода прямоугольников (4) получается, если отрезок интегрирования [a, b] разбить на п равных частей длиной:

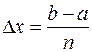
На каждом из отрезков разбиения [x_i-1, x_i] участок кривой у=f(x) заменяется отрезком прямой, параллельным оси абсцисс. Тогда:

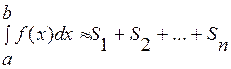
,где S₁, S₂,..., S_n - площади прямоугольников на каждом из отрезков разбиения. Отдельное слагаемое S_i; равно площади прямоугольника со сторонами ∆x и f(x), где i = 1, 2,..., n. Метод прямоугольников является простейшим, но и наименее точным. Более точно определенный интеграл может быть вычислен по формуле трапеций . В этом случае, в отличие от метода прямоугольников, на каждом из отрезков разбиения [x_i-1, x_i] участок кривой y=f(x) заменяется хордами, стягивающими концевые точки. Тогда, отдельное слагаемое интегральной суммы S_i, равно площади трапеции с основаниями f(x_i) и f(x_i-1) и высотой Ах, где i = 1, 2,..., n, то есть:

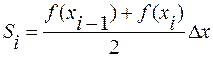
Складывая площади элементарных трапеций и приводя подобные члены, получаем формулу (5). Погрешность ∆ вычисления определенного интеграла по формуле трапеций S(n):

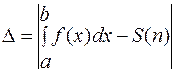
может быть оценена из выражения:

,

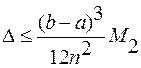где М₂ - максимальное значение модуля второй производной f"(x) подынтегральной функции y=f(х) на [a, b].

Рассмотрим пример вычисления интегралов по методу прямоугольников и методу трапеций. Пусть требуется вычислить интеграл с шагом ∆х=0,1:

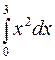
Аналитически данный интеграл может быть вычислен просто:

.

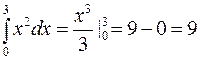Метод прямоугольников. Для нахождения определенного интеграла данным методом необходимо ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в диапазоне х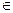[0; 3] с заданным шагом ∆ x=0,1.

1.Составляем таблицу данных х и f(х). Пусть столбец А будет хранить значения х, а второй столбец В – значения функции f(x). Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 - слово Функция, в ячейку А2 вводится первое значение аргумента - левая граница диапазона (0), а в ячейку A3 вводится второе значение аргумента - левая граница диапазона плюс шаг построения (0,1). Затем, выделив ячейки А2:АЗ, автозаполнением формируем все значения аргумента (за правый нижний угол блока А2:А3 курсор протягиваем до ячейки А32, до значения х=3).

2.Затем вводим значения подынтегральной функции, в ячейку В2 необходимо записать ее уравнение. Для этого табличный курсор необходимо установить в ячейку В2, ввести формулу =А2^2 и нажимаем Enter. В ячейке В2 появляется 0. Далее необходимо автозаполнением скопировать функцию из ячейки В2 в диапазон В2:В32 и в результате должна быть получена таблица данных для нахождения интеграла.

3.Теперь в ячейке ВЗЗ может быть найдено приближенное значение интеграла, для чего в ячейку ВЗЗ вводим формулу =0,1*, затем вызываем Мастер функций. В поле Функция выбираем функцию Сумм и нажимаем кнопку ОК. В рабочее поле диалогового окнаСУММ мышью определяем диапазон суммирования ВЗ:В32, заполняя поле Число1 и нажимаем кнопку ОК. В ячейке ВЗЗ появляется приближенное значение искомого интеграла (9,455). На рис.4.46. приведен фрагмент таблицы для вычисления интеграла.

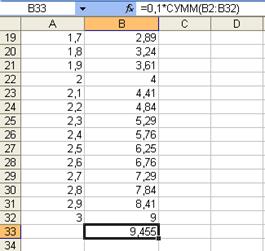
Рис.2.46.Вычисление интеграла

Сравнивая полученное значение с истинным значением вычисления интеграла - 9 можно отметить, что ошибка метода прямоугольников довольно значительна - 0,455.

Метод трапеций.Для нахождения определенного интеграла методом трапеций, как и в случае использования метода прямоугольников, значения подынтегральной функции f(х) должны быть введены в рабочую таблицу в диапазоне х 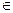[0; 3) с заданным шагом ∆ х=0,1. Поэтому этапы 1-3 полностью аналогичны этапам предыдущего решения. Поскольку таблица данных для нахождения интеграла уже введена, обсудим только этап 3. В ячейке В34 нужно вычислить приближенное значение интеграла по методу трапеций. Для этого в ячейку В34 вводим формулу =0,1*((В2 + В32)/2, затем вызываем Мастер функций. В рабочем поле диалогового окна Сумм определяем диапазон суммирования ВЗ:В31 и нажимаем кнопку ОК. В результате в ячейке В34 формируется приближенное значение искомого интеграла (9,005). Сравнивая полученное значение интеграла с истинным, можно отметить, что ошибка вычисления методом трапеций является вполне приемлемой - 0,005.

2.8.8. Решение дифференциальных уравнений

Использование дифференциальные уравнений находит широкое применение для компьютерного моделирования динамических процессов в автоматизированных системах управления, в механике, других математических моделях. Практическое применение в различных областях науки и техники находят как обыкновенные дифференциальные уравнения, так и уравнения в частных производных. Ниже будет рассмотрен пример решения обыкновенных дифференциальных уравнений с заданными начальными условиями, то есть для таких уравнений значения функции и ее производных до n-1 порядка являются известными при Х=0. Для обыкновенных дифференциальных уравнений,как правило, решается задача Коши, то есть задаются уравнения вида y¢=f (x,y) с начальными условиями x_0, y₀ при x₀ ≤ x ≤ x_кон.

Численное решение таких уравнений заключается в разбиении интервала х точками x_i с шагом h для i=1,2,…n и нахождении значений y_i по формуле y_i = y_i-1 + ∆y_i, где ∆y_i - приращение переменной у на каждом шаге.

Формула данного приращения определяется выбранным численным методом, Для метода Эйлера ∆y_{i =} h∙f(x_i,y_i), а в инженерных методах (Рунге-Кутта и других) она записывается более сложным образом. При этом уравнение 2-го и более высоких порядков предварительно должны быть сведены к нормальной системе обыкновенных дифференциальных уравнений 1-го порядка. Так уравнение y''=xy' +y² с начальными условиями x₀ =0, y₀ =3, y' =1 преобразуется к системе двух уравнений 1-го порядка:

y1' =y2, y2' =xy2 + y1²

с начальными условиями y1₀ = 3, y2₀ = 1.

Один из вариантов решения этой системы обыкновенных дифференциальных уравнений на интервале (0, 1) с шагом 0, 1 методом Эйлера приведен на рис.2.47.

Рис.2.47. Решение дифференциального уравнения

В столбце А создан диапазон изменения аргумента х от 0 до 1 с шагом 0, 1. Столбец В содержит вычисленные по формуле Эйлера значения Y1(=B2 + 0,1*C2), столбец С – значения Y2 (=C2 + 0,1*(A2*C2+B2^2)).

Графики изменения функций Y1(х) и Y2(х) представлены на диаграмме.

2.8.9. Финансовые вычисления в Excel

Для выполнения различных финансовых вычислений Excel содержит группу финансовых функций, реализуемых с помощью Мастера функций. Они включают такие функции как: вычисление амортизации активов, ставку доходности по вкладу, вычисление процентов за определенный инвестиционный период и многие другие. Ниже рассмотрим примеры реализации некоторых финансовых функций.