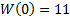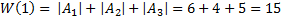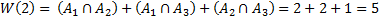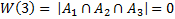Принцип включения-исключения
Этот метод (просеивания) известен еще с работ Бернулли. Решето Эратосфена – разновидность принципа включения-исключения.
Рассмотрим некоторое множество A1 как универсальное множество. Это множество обладает рядом свойств:
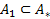 , которое обладает свойством
, которое обладает свойством 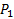
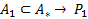
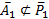 (Дополнение не обладает свойством
(Дополнение не обладает свойством 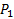 , а обладает свойством
, а обладает свойством 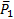 )
)
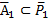
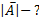
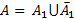
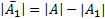 (1)
(1)
Наряду с 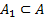 рассмотрим подмножество
рассмотрим подмножество 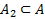 , которое обладает свойством
, которое обладает свойством 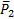
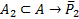
Требуется найти число подмножеств не обладающих ни 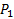 ни
ни 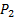 , то есть
, то есть 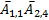 их объединения
их объединения 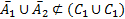
Если взять все элементы множества A и удалить все не обладающие ни 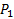 ни
ни 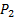 , то получим нужное нам свойство включения-исключения:
, то получим нужное нам свойство включения-исключения:
Найдем число элементов полученного множества (2) с помощью диаграмм Эйлера-Венна
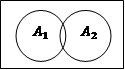 |
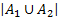 =
= 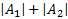 -
- 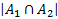
Поставим (3) во (2):
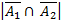 =
= 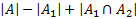
Формулу (4) можно распространить на любое число аналогично. Свойств, то есть можно считать, что:
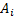
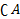 ,
, 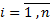 , причем, все элементы =
, причем, все элементы = 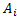 обладают свойством
обладают свойством 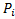 , а
, а 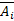 не обладают таким свойством, так как не существует взаимо-однозначных соответствий между элементами множества и подмножества, то есть они близки или похожи.
не обладают таким свойством, так как не существует взаимо-однозначных соответствий между элементами множества и подмножества, то есть они близки или похожи.
Раздел математики Фунтеры и категории.
Для уравнения (4) характерно следующее выражение:
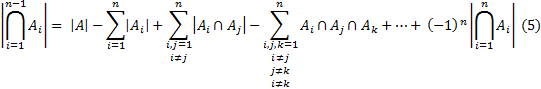
1)Множество 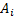 не обладает свойством
не обладает свойством 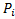 (
( 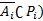
2) 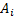 обладает свойством
обладает свойством 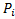 (
( 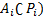 хотя бы одним
хотя бы одним
3) Здесь в (5) сумму ров. осущ. По всем сочетаниям без повторения, a представляет собой число элементов, обладающих по крайней мере 2-мя свойствами
4) По крайней мере 3-мя свойствами
5) Подмножество обладает всеми свойствами
Предположим для доказательства справедливости следующее соотношение:
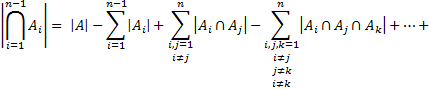
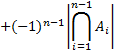
(6)
Считаем, что все элементы обладают 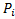 , и каждому члену выражения (6) добавим
, и каждому члену выражения (6) добавим 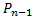 , тогда получим следующее выражение:
, тогда получим следующее выражение:
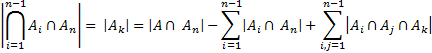
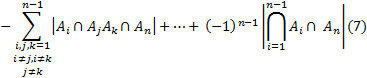
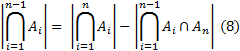
Требуется получить или найти число элементов, не обладающих ни одним из указанных свойств, но обладает свойством 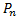
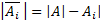 ?
?
В выражение (8) подставим (6) и (7) и получим после объединения и преобразования выражение (5).
Таким образом в итоге, предположив справедливость выражения (5) согласно принципу математической индукции она справедлива.
Пример: часто ставится задача найти число элементов A, обладающих k-заданным свойством.
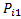 ,
, 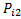 …
… 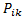 и не обладающее n-k свойствами
и не обладающее n-k свойствами 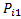 ,
, 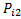 …
… 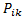
Сначала записываем формулу включения-исключения и проверяем ее на справедливость. Для этого каждому члену, полученного подмножества добавляем пересечение с многочленами 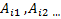 и получаем:
и получаем:
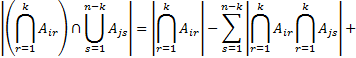
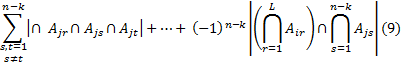
Пример: подмножество A= 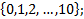
Свойства:
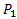 :
: 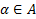 ,
, 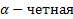
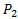 :
: 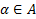 ,
, 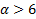
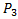 :
: 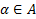
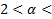 8
8
Найти 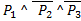 , т.е.
, т.е.
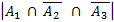 =
= 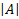 -
- 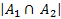 -(
-( 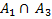 )+
)+ 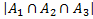 =
=
(0;6)
=6-2- 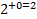
Формула (9) позволяет определить число элементов Aс заданными свойствами.
В некоторых случаях ставится задача найти число.
Это число обозначает W(k). Для этого введем сведущее обозначение :
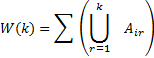
Т.е. здесь записано число элементов, обладающих k-
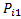 ,
, 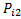 …
… 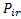
Произведем суммирование по всем k-сочетаниям без повторений из заданных n-подмножеств, тогда:
W(k)
W(0)= 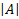
Исходя из (9) можно доказать, что W(k) есть число элементов, обладающих в точности k-свойствами и равными
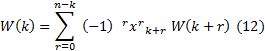
Если мы хотим найти число элементов, не обладающих некоторыми свойствами, мы можем прибавить r=0, при этом получим
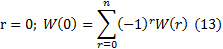
Пример: