Определение оптимального запаса поставки

Запасы играют как положительную, так и отрицательную роль в деятельности логистической системы. Положительная роль заключается в том, что они обеспечивают непрерывность процессов производства и сбыта продукции, являясь своеобразным буфером, сглаживающим непредвиденные колебания спроса, нарушение сроков поставки ресурсов, повышают надежность логистического менеджмента.

Негативной стороной создания запасов является то, что в них иммобилизуются значительные финансовые средства, которые могли бы быть использованы предприятиями на другие цели, например, инвестиции в новые технологии, исследования рынка, улучшение экономических показателей деятельности предприятия. Исходя из этого, возникает проблема обеспечения непрерывности логистических и технологических процессов при минимальном уровне затрат, связанных с формированием и управлением различными видами запасов в логистической системе.

Один из методов эффективного управления запасами – определение оптимальных партий поставок груза, который позволяет оптимизировать расходы на транспортировку, хранение груза, а также избежать избытка или недостатка груза на складе.

Оптимальный размер партии поставки q определяется по критерию минимума затрат на транспортировку продукции и хранение запасов.

Величина суммарных затрат рассчитывается по формуле (3.1):

С=С_mp+C_xp (3.1)

где С_mp – затраты на транспортировку за расчетный период (год), у.е.;

C_xp – затраты на хранение запаса за расчетный период (год), у.е.

Величина С_mp – определяется по формуле:

С_mp=n*c_mp (3.2)

где n – количество партий, доставляемых за расчетный период,

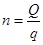(3.3)

c_mp – тариф на перевозку одной партии, у.е./партия.

Затраты на хранение определяются по формуле:

C_xp=q_cp*c_xp (3.4)

где q_cp – средняя величина запаса (в тоннах), которая определяется из предложения, что новая партия завозится после того, как предыдущая полностью израсходована.

В этом случае средняя величина рассчитывается по следующей формуле:

q_cp=q/2 (3.5)

Подставив выражения С_mp и С_mp в формулу (3.1), получим:

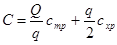(3.6)

Функция общих затрат С имеет минимум в точке, где ее первая производная по q равна нулю, т.е.

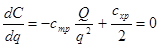(3.7)

Решив уравнение (3.7) относительно q получим оптимальный размер партии поставки:

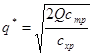(3.8)

В качестве размеров годового объема потребления продукции принимаем данные, полученные в результате прогнозирования методом скользящего среднего: Q=26,87 тыс. т/год; тариф на перевозку одной партии С_mp=100 y.e./т; расходы, связанные с хранением запаса С_хр=15 y.e./т. Подставив заданные значения, получим:

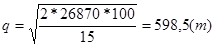
При этом общие затраты составят:

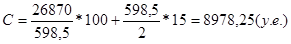
Решение данной задачи графическим способом заключается в построении графиков зависимости С_mp(q), C_xp(q) и C(q), предварительно выполнив необходимые расчеты по определению С_mp, С_хр и С.

Определим значение С_mp, С_хр и С при изменение q в пределах от 300 до 700 с шагом 100. Результаты расчетов занесем в таблицу 3.1.

Таблица 3.1.

Значение С_mp, С_хр и С

Размер партии,q
Затраты,y.e
Сmp
Схр
С

По данным табл.3.1 построены графики зависимости затрат (транспортных, складских и суммарных) от размера партии (Рисунок 3.1).

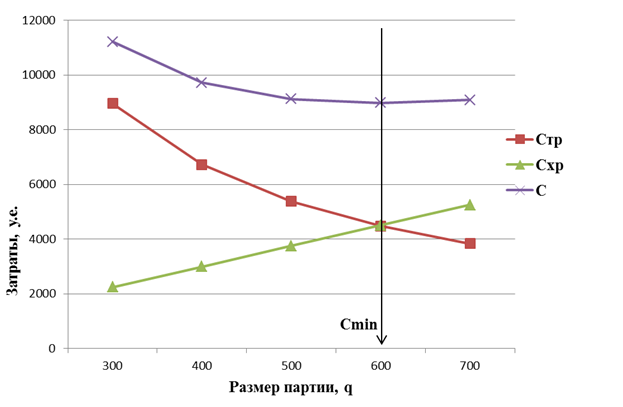
Рисунок 3.1 Зависимость затрат от размера партии

Анализ графиков на Рисунок 3.1 показывает, что затраты на транспортировку уменьшаются с увеличением размера партии, что связано с уменьшением количества рейсов. Затраты, связанные с хранением, возрастают прямо пропорционально размеру партии.

График суммарных затрат имеет минимум при значении q приблизительно равном 599 т, которое и является оптимальным значением размера партии поставки. Соответствующие минимальные суммарные затраты составляют 8110 y.e.

Произведем расчет оптимального размера партии в условиях дефицита при величине расходов, связанных с дефицитом С_деф=10 y.e./т.

В условиях дефицита значение q^*, рассчитанное по формуле (3.8) корректируется на коэффициент k, учитывающий расходы, связанные с дефицитом.

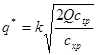(3.9)

Коэффициент k рассчитывают по формуле:

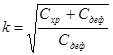(3.10)

С_деф – величина расходов, связанных с дефицитом;

принимаем С_деф=10y.e./т

Подставив значения, получим:

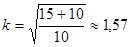
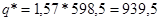т

Из этого следует, что в условиях возможного дефицита размер оптимального значения партии при заданных данных необходимо увеличить на 57%.