Основные теоретические положения булевой алгебры
Работа цифровых электронных схем подчиняется законам булевой алгебры (алгебры логики). Решение логических задач осуществляется с помощью логических элементов, базирующихся на математическом аппарате булевой алгебры, разработанной английским математиком Джорджем Булем (1815-1864), в которой все переменные величины (и аргументы, и функции) могут принимать только два логических значения: «1» (логическая единица) и «0» (логический ноль).
Понятия "1" и "0" являются условными, символизирующими состояния, например, релейного устройства: "включено", "выключено", высказывания «истинные» или «ложные». Как отмечалось, в цифровых электронных устройствах применяют сигналы двух уровней напряжения: низкого и высокого.
Логика называется положительной, если высокий потенциал отображает единицу, а низкий, – ноль. Если наоборот, высокий потенциал отображает ноль, а низкий, – единицу, то логика называется отрицательной. Данное правило называют логическим соглашением. Далее будет использоваться способ кодирования, называемый соглашением положительной логики.
В общем случае логическое устройство может иметь n входов и m выходов. Рассматривая входные сигналы х1, х2, ..., хn в качестве аргументов, можно соответствующие выходные сигналы представлять в виде функций уi=f(х0, х1, x2, ..., хn) с помощью элементарных операций алгебры логики.
Функции алгебры логики (ФАЛ), иногда называемые переключательными функциями, представляют в нескольких формах:
• в алгебраической (в виде математического выражения);
• в виде таблиц истинности или комбинационных таблиц;
• в виде временных диаграмм;
• встречается также абстрактный вид записи функций алгебры логики.
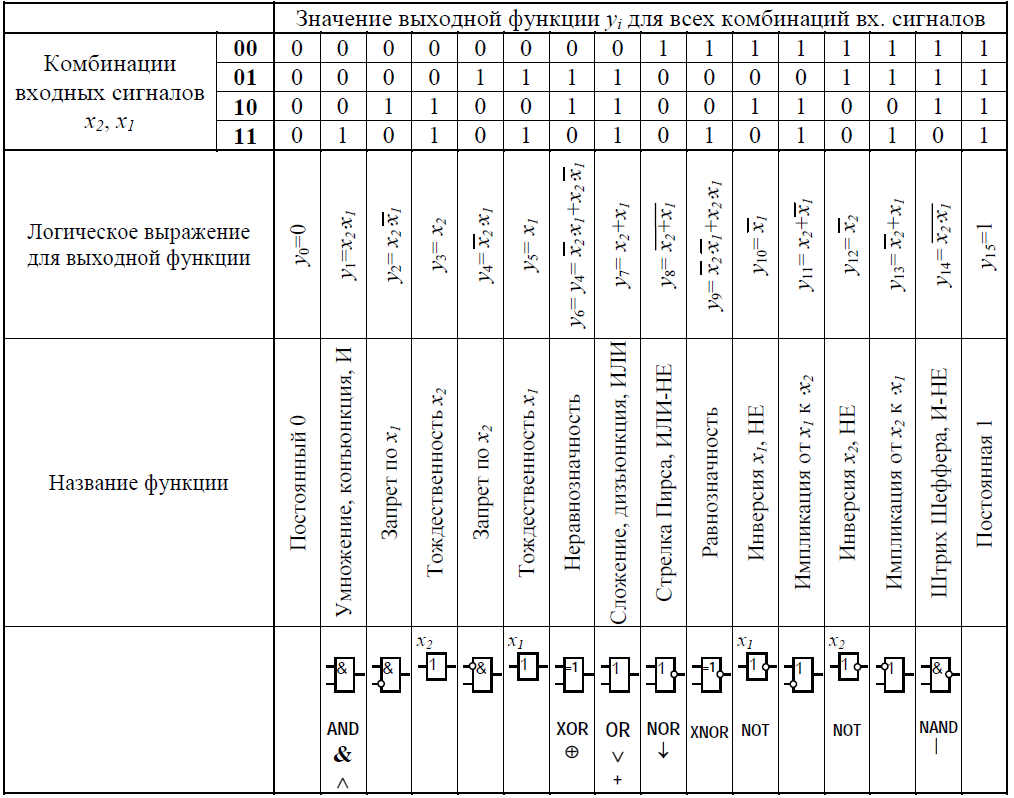
Для цифрового устройства с двумя входными переменными х1 и х2 возможно четыре варианта комбинаций аргументов (входных слов): 00, 01, 10 и 11 и шестнадцать различных выходных функций fi, (табл. 1).
Название и обозначение функции f, в какой-то мере отображает особенности выполнения логических операций. Нулевая f0 и единичная f15 функции тривиальны, функции f3, f5, f10 и f12 не зависят от одного из аргументов: f3=х2, f5=х1, f10=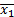 
и f12= 
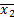. И только оставшиеся 10 функций являются функциями двух переменных.
Отметим, что многие функции имеют несколько названий. Например, логическая операция неравнозначности для функции f6 имеет название «исключающее ИЛИ», «сложение по модулю 2»; функция f7 имеет название логическое «сложение», «дизъюнкция», «ИЛИ». Для обозначения операций логических функций используются специальные символы. Например, в качестве знака операции ИЛИ-НЕ используется символ "↓" (стрелка Пирса), условное обозначение функции f8=х1↓х2; для операции И-НЕ принят символ "/" (штрих Шеффера), обозначение функции f14=х1/х2; для операции неравнозначности — символ ⊕ (сложения по модулю 2), обозначение функции f6=х1 ⊕ х2 и т. д.
Таблица 1 - Перечень всевозможных функций для логического устройства с двумя входами и одним выходом
