Отражение региональных связей в статических моделях. Статический межрегиональный МОБ (модель Мозеса-Ченери)
1. Территория РБ представляется из m регионов;
r – регион-производитель (поставщик); s – регион-потребитель (получатель) r,s = 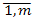 ; n – количество функционирующих в регионах отраслей; i – отрасль производитель; j – отрасль-потребитель i,j =
; n – количество функционирующих в регионах отраслей; i – отрасль производитель; j – отрасль-потребитель i,j = 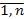
2. Межрегиональные и межотраслевые структурные взаимосвязи по производству, распределению и потреблению продукции отраслей в горизонтальном срезе (1-й и 2-й квадранты) представляются системой уравнений:
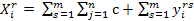 , r,s =
, r,s = 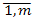 , i,j =
, i,j = 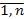
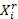 - объем производства продукции (валовая продукция) отрасли в регионе r;
- объем производства продукции (валовая продукция) отрасли в регионе r;
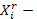 объем продукции i-й отрасли, поставляемой из региона r в регион s для производства продукции j-й отрасли;
объем продукции i-й отрасли, поставляемой из региона r в регион s для производства продукции j-й отрасли;
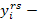 объем продукции i-й отрасли, поставляемой из региона r в регион s для конечного использования.
объем продукции i-й отрасли, поставляемой из региона r в регион s для конечного использования.
Основное предположение: региональная структура потребления продукции устойчива.
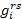 – доля продукции i-й отрасли, произведенной регионом r, в производственном и непроизводственном потреблении региона s:
– доля продукции i-й отрасли, произведенной регионом r, в производственном и непроизводственном потреблении региона s: 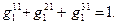
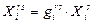
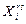 - произведенная в регионе r продукция i-й отрасли и отправленная в регион s для производственного и непроизводственного потребления.
- произведенная в регионе r продукция i-й отрасли и отправленная в регион s для производственного и непроизводственного потребления.
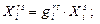
где 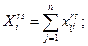
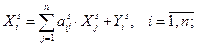
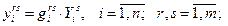
С учетом вышеизложенных формул получится модель межрегионального МОБа:
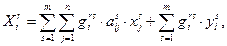
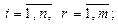
В матричной записи выглядит так: 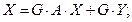
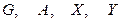 - блочные матрицы. Из этого следует
- блочные матрицы. Из этого следует 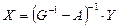
Модель динамического МОБа для замкнутого производства как система линейных однородных дифференциальных уравнений. Алгоритм численного решения динамической модели МОБа для замкнутой экономической системы. Экономическая интерпретация аналитического решения.
Замкнулая си-ма – эк.с-ма, в которой все отрасли являются производящими, вся произведенная продукция потребляется этими же производящими отраслями. В замкнутой модели объем затрат каждого сектора равен объему произведенной.
1. Простейшая динамическая модель МОБа с постоянными коэффициентами выглядит так:
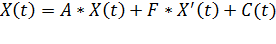 , (1)
, (1)
где X(t) = [Xj(t)] - вектор - столбец объемов производства в году t (t=0,1,2,…,T), (j=1,2,…,n);
X’(t) = [X’j(t)] - вектор – столбец абсолютных приростов производства в году t (вектор – столбец производных функций);
C(t) = [Cj(t)] - вектор – столбец потребления (включая непроизводственное потребление) в году t;
A=(aij)- матрица коэффициентов прямых материальных затрат;
F=(fij)- матрица коэффициентов капиталоемкости приростов производства.
2. Неоднородная система дифференциальных уравнений (1) эквивалентна системе: 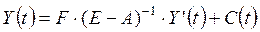 , (2)
, (2)
где 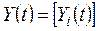 - вектор – столбец конечного использования продукции отраслей в году t, (t=0,1,2,…,T), (i=1,2,…,n);
- вектор – столбец конечного использования продукции отраслей в году t, (t=0,1,2,…,T), (i=1,2,…,n); 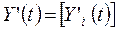 - вектор – столбец абсолютных приростов конечной продукции по отраслям.
- вектор – столбец абсолютных приростов конечной продукции по отраслям.
3.Матрица А продуктивна или неразложима, матрица F невырожденна 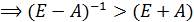 ,
, 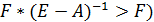 (поэлементно).
(поэлементно).
4. Решения системы (2) при 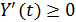 в силу неотрицательности матриц
в силу неотрицательности матриц 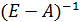 и
и 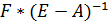 гарантируют, что
гарантируют, что 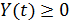 ,
, 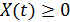 ,
, 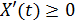 .
.
5. Динамическая модель замкнутой производственно-экономической с-мы, представляющей собой линейную однородную систему дифференциальных уравнений выглядит так (в матричной записи): 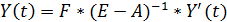 (3)
(3)
Решение с-мы (3) характеризует предельные технологические возможности развития производства при заданных матрицах А и F, когда все ресурсы ВВП направляются на расширенное воспроизводство.
6.Общее решение системы (3) имеет следующий аналитический вид: 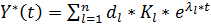 (4)
(4)
Параметры аналитического решения (4) 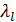 ,
, 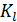 ,
, 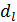 получаются в следующей последовательности:
получаются в следующей последовательности:
a) 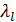 - корни характеристического уравнения n-го порядка:
- корни характеристического уравнения n-го порядка: 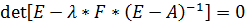 (5)
(5)
б) 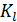 - соответствующие
- соответствующие 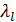 собственные векторы матрицы
собственные векторы матрицы 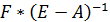 ,
, 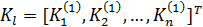 , и являются решениями (бесконечными) алгебраической системы однородных уравнений:
, и являются решениями (бесконечными) алгебраической системы однородных уравнений: 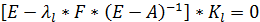 (6)
(6)
где, 0 (“нуль”) – нулевой вектор – столбец размерности n×1;
в) 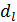 - постоянные, определяемые из системы уравнений:
- постоянные, определяемые из системы уравнений: 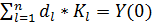 (7)
(7)
где Y(0) – вектор–столбец конечного использования продукции отраслей в базисном году.
В общем случае решение (7) содержит несколько отличных от нуля компонент 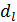 . Поэтому, единственная траектория системы (3), выходящая из начальной точки Y(0), представляет собой комбинацию экспонент, растущих с различными темпами.
. Поэтому, единственная траектория системы (3), выходящая из начальной точки Y(0), представляет собой комбинацию экспонент, растущих с различными темпами.
7. Пусть 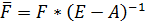 ,
, 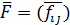 . Для матрицы
. Для матрицы 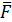 существует теорема Перрона:
существует теорема Перрона:
а) матрица 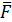 имеет положительное собственное число
имеет положительное собственное число 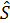 , которое превосходит модули всех остальных собственных чисел;
, которое превосходит модули всех остальных собственных чисел;
б) для 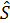 , называемого корнем Фробениуса – Перрона, выполняется условие:
, называемого корнем Фробениуса – Перрона, выполняется условие: 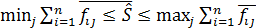 .
.
в) собственному числу 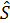 отвечает единственный собственный вектор
отвечает единственный собственный вектор 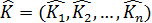 , все координаты которого строго положительны и удовлетворяют условию:
, все координаты которого строго положительны и удовлетворяют условию:
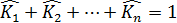 .
.
8. Так как 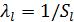 ,
, 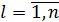 ,
, 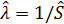 - соответствует вектор
- соответствует вектор 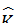 .
.
9. Значение 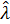 в межотраслевой динамической модели находит объяснение технологического темпа прироста ВВП, а вектор
в межотраслевой динамической модели находит объяснение технологического темпа прироста ВВП, а вектор 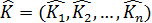 - отраслевой структуры ВВП.
- отраслевой структуры ВВП.
| Конечное использование капитальных вложений (инвестиц) | ||||
| У’ | Валовой выпуск | |||
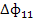 | 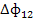 | 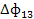 | У1’ | X1 |
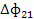 | 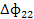 | 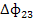 | У2’ | X2 |
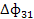 | 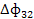 | 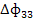 | У3’ | X3 |
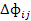 – поставка инвестиционных товаров из i-отрасли в j-ю (в сфере услуг =0).
– поставка инвестиционных товаров из i-отрасли в j-ю (в сфере услуг =0).
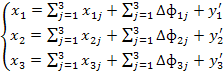 (1)
(1)
Чтобы использовать МОБ для прогноза, вводят понятие приростной фондоемкости – объем инвест. продукта i-отрасли, кот. необходима для обеспечения прироста производства j-й отрасли на единицу.
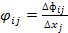 , i,j=
, i,j= 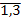 . (2)
. (2)
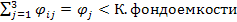 (если есть технологич. изменения, если нет, то величины равны).
(если есть технологич. изменения, если нет, то величины равны).
(1) с учетом (2):
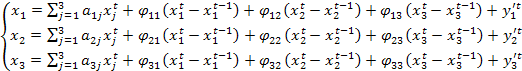
Можно реализовать след. сценарий:
Конечный спрос без кап вложений 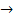 валовой выпуск + структура инвестиций.
валовой выпуск + структура инвестиций.
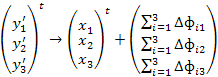
Допущения модели:
1) Прирост производства 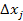 обеспечивается полностью за счет кап вложений в эту отрасль.
обеспечивается полностью за счет кап вложений в эту отрасль.
2) Прирост производства за период (t,t-1) обусловлен вложениями этого же периода. Если существует лаг, то используют модель Неймана.
Система уравнений, каждое из которых выражает требование баланса в разрезе каждой отрасли между производимым количеством продукции за период времени (t, t-1) и совокупной потребностью в этой продукции в периоде времени (t). В дин.модели произв-е капвложения выделяются из состава конечной продукции, исследуется их структура и влияние на рост объема производства: 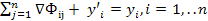 . Модель отчетного МОБ перепишется в виде:
. Модель отчетного МОБ перепишется в виде: 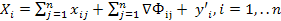 . В отличие от потоков промеж.затрат потоки капитальных вложений связаны не со всей величиной выпуска продукции, а обусловлены приростом продукции, причем в базовой модели предполагается, что прирост продукции текущего периода обусловлен вложениями этого же периода, т.е.
. В отличие от потоков промеж.затрат потоки капитальных вложений связаны не со всей величиной выпуска продукции, а обусловлены приростом продукции, причем в базовой модели предполагается, что прирост продукции текущего периода обусловлен вложениями этого же периода, т.е. 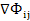 =
= 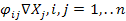 . Коэффициент
. Коэффициент 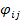 называется коэффициент вложений или коэффициент приростной фондоемкости и показывает какое количество продукции i -й отрасли должно быть вложено в j -ю отрасль для увеличения производственной мощности j -й отрасли на единицу. Коэффициент рассчитывается по формуле:
называется коэффициент вложений или коэффициент приростной фондоемкости и показывает какое количество продукции i -й отрасли должно быть вложено в j -ю отрасль для увеличения производственной мощности j -й отрасли на единицу. Коэффициент рассчитывается по формуле: 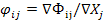 .Прогнозная динамическая модель МОБ запишется в виде:
.Прогнозная динамическая модель МОБ запишется в виде: 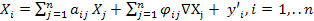 . или
. или 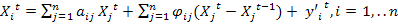 . После преобразования:
. После преобразования: 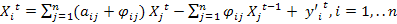 .
.
Модель позволяет реализовать сценарий: 
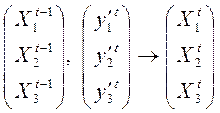
Предположения модели: 1. полная загрузка производственных мощностей и прирост производства 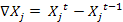 осуществляется за счет капвложений
осуществляется за счет капвложений 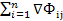 ; 2.прирост производства за период (t, t-1) обусловлен вложениями этого же периода; 3. величина капвложений пропорциональна приросту продукции.
; 2.прирост производства за период (t, t-1) обусловлен вложениями этого же периода; 3. величина капвложений пропорциональна приросту продукции.
