Дисперсия в ступенчатых одномодовых волокнах

Как указывалось ранее, в многомодовых ступенчатых волокнах межмодовая дисперсия налагает серьезные ограничения на информационную пропуск­ную способность. Однако ее можно исключить, если спроектировать волокно так, чтобы в нем могла распространяться только одна мода НЕ₁₁.

Условие одномодовости волокна

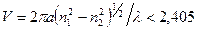(2.51)

и может быть достигнуто увеличением рабочей длины волокна, уменьшением диаметра сердцевины либо уменьшением разности показателей преломления между сердцевиной и оболочкой.

Таким образом, в одномодовых ОВ распространяется только одна мода и уширение импульсов определяется хроматической дисперсией, состоящей из материальной и волноводной дисперсий.

Для оценки хроматической дисперсии в одномодовых ОВ введем не­большую коррекцию, т. е. представим параметр материальной дисперсии Y_м следующим образом:

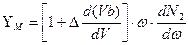. (2.52)

По аналогии введем также параметры волноводной Y_В и материальной Y_Д дисперсий:

,

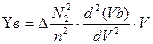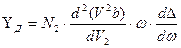. (2.53) и (2.54)

Тогда дисперсия

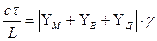, (2.55)

где .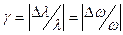

Чтобы оценить значение волноводной дисперсии Y_В в (2.53), необходимо знать значение

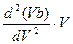моды НЕ₁₁нормализованная характеристика b₁₁которой представлена на рис. 2.20.

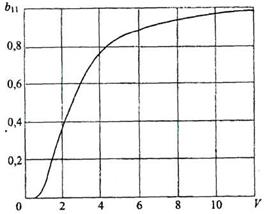
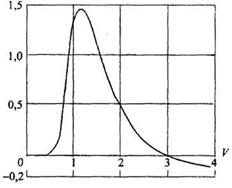
Рис. 2.20. Зависимость b от V моды НЕ₁₁для ступенчатого ОВ

Используя зависимость (рис. 2.20), можно определить значения 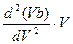моды НЕ₁₁ для ступенчатого ОВ (рис. 2.21).

Для b(V) при 1,5 < V < 2,4 используется приближение вида

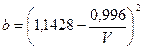, (2.56)

после дифференцирования которого, получаем

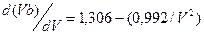, (2.57)

откуда

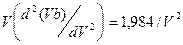(2.58)

и окончательно получаем

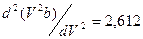(2.59)

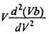Чтобы определить относительные величины всех слагаемых в (2.53), рас­смотрим в качестве примера одномодовое волокно, оболочка которого изготов­лена из чистого кварца, а сердцевина из кварца, легированного германием.

Рис. 2.21. Зависимость 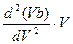от V моды НЕ₁₁ для ступенчатого ОВ

Исследуем их поведение на четырех длинах волн: 0,85; 1,27; 1,35 и 1,55 мкм в предположении, что волокно спроектировано таким образом, что на каждой длине волны ∆ = 0,005, a V=0,2. Предположим также, что на каждой длине волны имеются лазерные источники излучения с относительной шири­ной спектральной линии γ= 0,003. Для получения ∆ = 0,005 потребуется кон­центрация примеси германия около 4,5%.

При V =2 получаем следующие значения величин, определяемых форму­лами (2.57)-(2.59):

; ; .

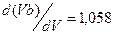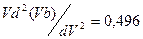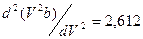Таблица 2.6

Параметры волокна на различных длинах волн

λ, мкм	2а, мкм (при V=2)	n2	N2	N22 / n2	Yм	Yω	Yd	Yобщ	γ	τ/L= Yобщ∙ γ/c, пс/км
0,85 1,27 1,35 1,55	3,72 5,58 5,94 6,83	1,453 1,448 1,447 1,444	1,466 1,462 1,462 1,462	1,48 1,48 1,48 1,48	0,0215 0,00015 -0,0028 -0,0100	0,0037 0,0037 0,0037 0,0037	0,0008 -0,0008 -0,0001 -0,008	0,026 0,003 -0,0001 -0,008	0,003 0,003 0,003 0,003

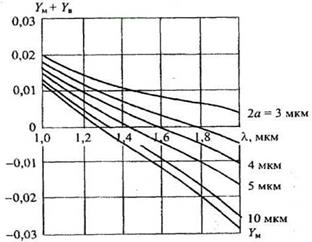
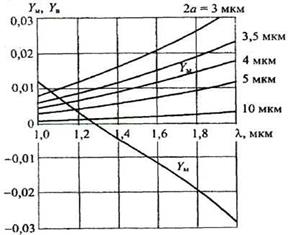
Рис. 2.22. Сочетание материальной и волноводной дисперсий в одномодовом волокне

Результаты расчета дисперсионных параметров представлены в табл. 2.6.

Видно, что длине волны 0,85 мкм параметр Y_мпреобладает над всеми другими слагаемыми в (2.55). Однако, как было показано ранее, с увеличением длины волны значение Y_м уменьшается до нуля, а затем изменяет знак на длине волны порядка 1,28 мкм. На более длинных волнах волноводная и материаль­ная дисперсии будут компенсировать друг друга. На практике это означает, что для одномодового волокна минимум общей дисперсии сдвигается в сторону более длинных волн, в нашем примере к 1,35 мкм.

Степень этого смещения зависит от величины Y_B, а следовательно, от кон­струкции волокна.

С учетом (2.58) находим

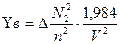, (2.60)

где 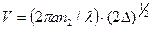. (2.61)

Окончательно

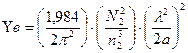. (2.62)

Таким образом, если надо увеличить волноводную дисперсию, необходи­мо уменьшить значение V для волокна на рабочей длине волны, а это требует уменьшения диаметра сердцевины. Чтобы довести общую дисперсию до нуля на длине волны 1,55 мкм, соответствующей минимуму потерь, необходимо иметь параметр Y_B = 0,0116. В таком случае требуемое значение величины Vd²(Vb)/dV ² =0,0116/(0,0050∙48)= 1,57.

Из рис. 2.21 видно, что она больше своего максимального значения и, следовательно, требуемое условие может быть удовлетворено только при уве­личении ∆ и уменьшении а. При уменьшении значения V до 1,5, нужно увеличить значение ∆ до 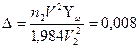и уменьшить диаметр сердцевины .

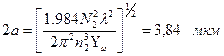На рис. 2.22 показано, как можно сдвинуть дисперсионный минимум в сторону длинных волн путем уменьшения диаметра сердцевины, а значит, и нормализованной частоты V:кривые построены для Y_м и Y_B no формулам (2.52) и (2.62) соответственно.

Рассмотренные эффекты подтверждают факт создания одномодовых ОВ, в которых минимум дисперсии совпадает с минимумом потерь в области 1,55 мкм.