Анализ характеристик программных модулей с помощью управляющего графа

Для количественной оценки сложности программных модулей используется графовая модель, представляющая собой направленный граф с циклами, вершинами которого являются линейные участки программы, а дугами - управляющие связи между линейными участками. Анализируя такой граф, можно обнаружить неисполняемые участки программы, получить все циклы (явные, заданные операторами цикла, и неявные, построенные с помощью условных операторов), обнаружить входы «сбоку» в структурированные конструкции (например, вход в тело цикла, минуя заголовок), наличие нескольких входов и выходов из процедур, отступления от стандартов программирования и т.д., что существенно важно при анализе технологической безопасности программ и, в частности, при определении критичных путей их выполнения.

Количественная оценка сложности программы при помощи управляющего графа вычисляется [Лип0] как сумма V=e-n+2p, где e – число дуг, n - число вершин, p - число связных компонент графа. Оценкой сложности можно пользоваться и при проектировании программ: если сложность превосходит некоторое критическое значение, то программу целесообразно разбить на более мелкие модули для упрощения ее понимания и отладки. В качестве критической сложности обычно принимают значение 10 единиц.

Основные алгоритмы, используемые на данном этапе, связаны с преобразованием управляющего графа, его анализом и построением возможных путей реализации программы. При этом преобразование графа основывается на понятии структурного дерева программы, вершинам которого соответствуют структурированные конструкции программы (условные операторы, циклы и последовательные операторы), вершины управляющего графа и неструктурируемые конструкции.

Неструктурируемой конструкцией графа называется его компонент, не содержащий других конструкций с одним входом и одним выходом и не принадлежащий множеству структурированных конструкций.

Вычисление управляющего графа обычно осуществляется при трансляции программы, но, к сожалению, большинство компиляторов не выдает его программисту в качестве результата своей работы.

При использовании ассемблеров управляющий граф легко может быть восстановлен по машинному коду [Лип0],а для языков высокого уровня необходимо создавать нетривиальные программы, сканирующие исходный текст и выделяющие управляющие конструкции языка.

Однако при разработке методики определения критических путей управляющих программ с позиции обеспечения технологической безопасности можно сделать допущение, что управляющий граф программы известен.

Алгоритм построения структурного дерева программы (алгоритм А) сводится к реализации следующей конструкции. Построение структурного дерева программы осуществляется параллельно со сверткой управляющего графа, когда выделенная конструкция заменяется одной вершиной. Для краткости управляющий граф на очередном этапе свертки будем называть графом программы. Таким образом, граф программы будет последовательно преобразовываться в G₀,G₁,..., где G₀ - исходный управляющий граф последовательности - граф, состоящий из одной вершины.

Алгоритм А

А₁. В структурном дереве образуются вершины простейшего типа, которым соответствуют вершины исходного управляющего графа.

А₂. В графе программы ищется структурированная конструкция. Если такой нет, то выполняется переход к шагу А₄.

А₃. В дереве образуется вершина структурированной конструкции. Эта конструкция сворачивается в вершину, тип которой указывается. Выполняется переход к шагу А₂.

А₄. Если в графе осталась только одна вершина, то работа алгоритма заканчивается.

А₅. В графе выделяется неструктурируемая конструкция и в структурном дереве образуется вершина соответствующего типа. Конструкция в графе сворачивается, после чего выполняется переход к шагу А₂.

Построение структурного дерева выполняется от элементов, представляющих вершины управляющего графа, к элементу, представляющему всю программу целиком. Используя понятие структурного дерева программы, можно рассчитать существенную сложность программы EV: 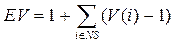S(V(i)-1), где NS - множество вершин неструктурируемого типа в структурном дереве; V(i) - топологическая сложность конструкции, соответствующей i-й вершине дерева.

Вычисление V(i) производится на шаге А₅ алгоритма по формуле V(i)=e(i)-n(i)+2, где e(i) - количество дуг, а n(i) - количество вершин рассматриваемой конструкции.

Таким образом, построение структурного дерева программы при реализации алгоритма А позволяет получить численные оценки сложности, которые в дальнейшем используются при определении критических путей, требующих наиболее тщательного обследования с позиций технологической безопасности программ.