Пример выполнения задания «Оптимизационные задачи в MS Excel»
Средство анализа Поиск решения применяется для подбора оптимального решения при заданных ограничениях. Формулировка задач, решаемых при помощи этого средства обычно представляет собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Обычно при помощи надстройки Поиск решения решаются следующие задачи:
¾ Ассортимент продукции (максимизация выпуска товаров при ограничениях на сырье для производства этих товаров).
¾ Составление штатного расписания для достижения наилучших результатов при наименьших расходах.
¾ Планирование перевозок (минимизация затрат на транспортировку товаров при условии удовлетворения потребностей потребителей).
¾ Составление смеси (получение заданного качества смеси при наименьших расходах)
Все эти задачи обладают следующими свойствами:
1. Наличие единственной цели.
2. Наличие ограничений, выражающихся, как правило, в виде неравенств.
3. Наличие набора входных значений-переменных, непосредственно или косвенно влияющих на ограничения и на оптимизируемые величины.
Правильная формулировка ограничений является самой ответственной частью при создании модели для поиска решения, например:
1. Если в модели в наличии несколько периодов времени, величина материального ресурса на начало следующего периода должна равняться величине этого ресурса на конец предыдущего периода.
2. В модели поставок величина запаса на начало периода плюс количество полученного должна равняться величине запаса на конец периода плюс количество отправленного.
3. Некоторые величины в модели по своему физическому смыслу не могут быть отрицательными либо дробными.
Ограничения имеют тот же синтаксис, что и логические формулы. Но, если в найденном решении логические формулы будут выполнены точно, то ограничения – с некоторой возможной погрешностью. Величина этой погрешности задается параметром Относительная погрешность и по умолчанию равна 0,000001.
Пример. Компания имеет два склада, на которых хранится товар, и три магазина, где этот товар реализуется. Задача заключается в строгом выполнении плана, который компания получает каждый день. В качестве транспортного средства компания использует автомобиль, который не позволяет перевозить всю партию за раз. Составить с учетом выдаваемого компании плана такой маршрут движения, чтобы на выполнение всего задания уходило минимум времени и сил.
Составление математической модели.
Сначала необходимо проделать подготовительную работу, а именно - определить тарифы на каждом участке будущего оптимального плана перевозок. Поскольку компания заинтересована в том, чтобы делать свою работу максимально быстро, то в качестве тарифов в данной задаче выступает время, потраченное на перевозку единицы товара из n-го склада в m-ую контору. При помощи карты Минска, с учетом времени на заправку автомобиля, компания оценила среднее время перевозки товара из каждого склада в каждый магазин. В результате была составлена таблица с исходными данными (табл.2.5).
Таблица 2.5
Время на перевозку
| Склад\Магазин | Магазин №1 | Магазин №2 | Магазин №3 | Есть на складах |
| Склад №1 | ||||
| Склад №2 | ||||
| Потребность | 47/50 |
Данная транспортная задача относится к типу задач с неправильным балансом (47<>50). Далее задачу необходимо формализировать, т.е. записать в виде уравнений (формул). Пусть X – количество единиц товара, перевозимых из каждого склада в каждый магазин. Тогда X11 - количество единиц товара, перевозимых из первого склада в первый магазин, X12 - количество единиц товара, перевозимых из первого склада во второй магазин, и т.д. Поскольку задача с неправильным балансом, то необходимо ввести также фиктивный магазин. Все переменные представлены ниже (табл. 2.6).
Таблица 2.6
Количество перевозимых товаров
| Склад\Магазин | Магазин №1 | Магазин №2 | Магазин №3 | Фиктивный | Есть на складах |
| Склад №1 | X11 | X12 | X13 | X14 | |
| Склад №2 | X21 | X22 | X23 | X24 | |
| Потребность | 50/50 |
Теперь все готово для составления системы уравнений и целевой функции, определяющей время выполнения плана перевозок и направленной на минимум. По смыслу ясно, что количество единиц товара, привезенных с каждого склада в магазин, в сумме должно равняться потребности этого магазина. Т.е.
X11+ X21=15
X12+ X22=12
X13+ X23=20
X14+ X24=3
Аналогично получаем следующие условия:
X11+X12+X13+X14=20
X21+X22+X23+X24=30
Целевая функция определяет время выполнения намеченного плана транспортировки товара. Поэтому:
E=5* X11 + 20* X12 + 8* X13 + 10* X21 + 15* X22 + 12* X23 → min
Тарифы на доставку товара в виртуальный магазин принимаются равными нулю, поэтому слагаемое (0*X14+0*X24) в записи формулы для целевой функции можно опустить.
Выбор метода решения.
Итак, в ячейки строки с целевой функцией запишем коэффициенты перед переменными, входящими в целевую функцию. Так же поступим и cо всеми ограничениями в виде равенств (в столбце "L" записывается правая часть уравнений). В столбце с решением "J" в каждую ячейку введем формулу вида: =СУММПРОИЗВ(Bn:Gn;B2:G2), где n изменяется от 3 до 9. Затем открываем окно диалога «Поиск решения» и записываем все ограничения (рис. 2.6).
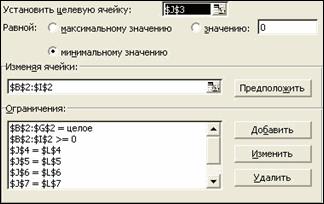
Рис. 2.6. Окно диалога «Поиск решения»
Нажимаем на кнопку "Выполнить".
Оптимальный план перевозок груза выглядит следующим образом: с первого склада нужно переправить 15 ед. груза в первый магазин и 5 ед. груза в третий магазин, а со второго - 12 ед. груза во второй и 15 ед. груза в третий магазин. На все это компания будет тратить 475 минут (7 часов и 55 минут). Это оптимальный вариант.
