Подготовка данных для программы W_TKЗ включает составление схемы замещения, расчет параметров элементов и подготовку файлов исходных данных
Схема замещения для расчета симметричных КЗ приведена на рисунке 4.1.
В расчетную схему введены все источники, все связи между ними и элементы, по которым нужно определить токи коротких замыканий. Если в расчетной схеме имеются замкнутые контуры, то токи коротких замыканий нужно рассчитывать и для схемы с разомкнутым контуром, так как при этом через некоторые аппараты и токопроводы могут протекать наибольшие токи коротких замыканий.
Схема замещения, представленная на рис 4.1, отличается от схемы для расчета нормальных режимов только наличием сопротивлений и ЭДС источников (узлы 8, 9). ЭДС источников определяются программой, а сопротивления должны быть заданы в качестве исходных данных.
Рисунок 4.1 Схема замещения для расчета симметричных КЗ
Сопротивление источника в узле 7 (электростанция А). На электростанции А установлены блоки генератор-трансформатор, поэтому нужно определить эквивалентное сопротивление блока:
Сопротивление источника в узле 8 (система) определяется по заданному току КЗ в узле 8 со стороны системы Iкз = 21 кА , Uн = 110 кВ
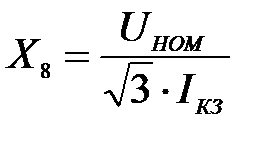=3,02 Ом
Определение сопротивления генераторов для узла «7»
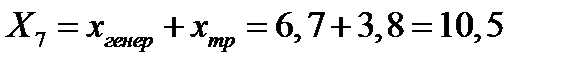Ом
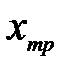-из таблицы 1.4
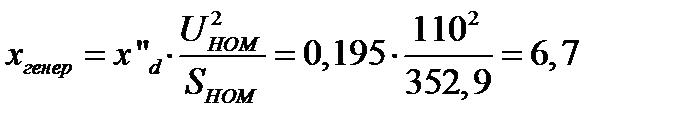Ом
где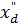 
-из таблицы 1.3
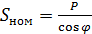=352,9 МВА.
где P–мощность генератора из таблицы 1.3,
- из таблицы 1.3.
Все данные, необходимые для подготовки файла исходных данных для расчета трехфазных КЗ приведены в таблицах 4.1 и 4.2. От данных для расчета нормальных режимов они отличаются только тем, что добавлены сопротивления источников, а мощности генераторов взяты по результатам расчетов нормальных режимов (таблицы 3.3 и 3.4).
Таблица 4.1 - Исходные данные расчета трехфазных КЗ в максимальном режиме
| Число узлов | ||||||||||||||
| Число ветвей | ||||||||||||||
| Информация об узлах | ||||||||||||||
| N | VNOM | PN | QN | PG | QG | RG | XG | |||||||
| 110,00 110,00 110,00 110,00 110,00 110,00 110,00 110,00 110,00 110,00 | 10,33 13,11 20,19 12,87 15,93 0,00 0,00 0,00 0,00 17,77 | 4,03 5,28 10,24 6,18 7,09 0,00 0,00 0,00 0,00 7,65 | 0,00 0,00 0,00 0,00 0,00 0,00 73,86 0,00 0,00 | 0,00 0,00 0,00 0,00 0,00 0,00 11,65 24,16 0,00 0,00 | 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 | 0,00 0,00 0,00 0,00 0,00 0,00 10,5 3,02 0,00 0,00 | ||||||||
| Информация о ветвях | ||||||||||||||
| i | j | r | x | g | b | kt | ||||||||
| 2,33 | 7,85 | 0,00 | 54,49 | 0,00 | ||||||||||
| 3,83 | 12,92 | 0,00 | 89,64 | 0,00 | ||||||||||
| 3,3 | 11,15 | 0,00 | 77,33 | 0,00 | ||||||||||
| 3,83 | 12,92 | 0,00 | 89,64 | 0,00 | ||||||||||
| 3,9 | 13,18 | 0,00 | 91,41 | 0,00 | ||||||||||
| 3,38 | 11,4 | 0,00 | 79,1 | 0,00 | ||||||||||
| 4,1 | 13,68 | 0,00 | 94,92 | 0,00 | ||||||||||
| 1,35 | 4,56 | 0,00 | 31,64 | 0,00 | ||||||||||
| 0,68 | 2,28 | 0,00 | 15,82 | 0,00 | ||||||||||
| 0,68 | 2,28 | 0,00 | 15,82 | 0,00 | ||||||||||
| 2,19 | 43,35 | 0,00 | 16,94 | 0,00 | ||||||||||
Таблица 4.2 Исходные данные расчета трехфазных КЗ в минимальном режиме.
| Число узлов | ||||||||
| Число ветвей | ||||||||
| Информация об узлах | ||||||||
| N | VNOM | PN | QN | PG | QG | RG | XG | |
| 110,00 110,00 110,00 110,00 110,00 110,00 110,00 110,00 110,00 110,00 | 3,1 3,94 6,05 3,86 7,96 0,00 0,00 0,00 0,00 8,89 | 0,25 2,8 2,07 0,95 2,72 0,00 0,00 0,00 0,00 3,4 | 0,00 0,00 0,00 0,00 0,00 0,00 11,9 20,1 0,00 0,00 | 0,00 0,00 0,00 0,00 0,00 0,00 4,49 0,19 0,00 0,00 | 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 | 0,00 0,00 0,00 0,00 0,00 0,00 10,5 3,02 0,00 0,00 | ||
АЛГОРИТМ РАСЧЕТА АВАРИЙНЫХ РЕЖИМОВ
ПРИ ТРЕХФАЗНЫХ КЗ
В основу алгоритма, реализованного в программе , положены следующие обычно принимаемые допущения: сохранение симметрии системы, отказ от учета качаний и АРВ генераторов, отказ от учета насыщения магнитных систем элементов сети, приближенный учет нагрузок. В зависимости от стадии переходного процесса, нагрузку можно представить либо некоторым постоянным сопротивлением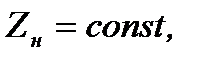 
либо постоянной ЭДС 
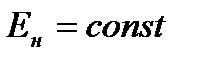за сопротивлением 
;
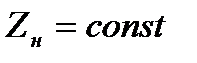При принятых допущениях все элементы электрической сети становятся линейными, поэтому в качестве математической модели сети можно использовать узловые уравнения в форме баланса токов:
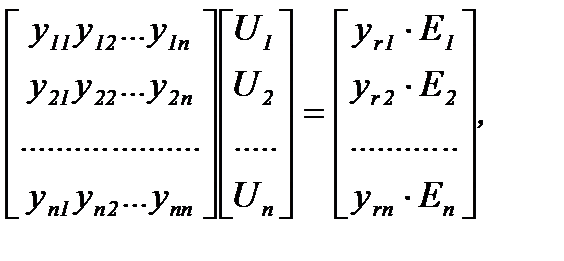(4.1)
где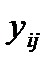 
, 
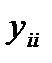- собственные и взаимные проводимости узлов, элементы матрицы узловых проводимостей [y]; 
.
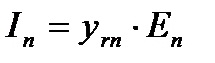Вектор-столбец заданных величин содержит в строках, соответствующих нагрузочным узлам, нули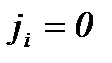 
, а в строках, соответствующих узлам с генераторами, 
.
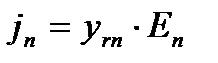При трехфазном коротком замыкании в одном из узлов сети напряжение соответствующего узла становится равным нулю, количество неизвестных и уравнений (4.1) уменьшается на единицу. Система из (n-2) линейных узловых уравнений:
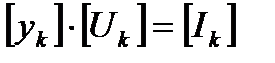, (4.2)
решение которой дает значения неизвестных напряжений в узлах сети при коротких замыканиях, является математической моделью электрической сети в аварийном режиме при принятых упрощениях. Уравнения (4.2), соответствующие коротким замыканиям в различных узлах сети, получаются из (4.1) вычеркиванием столбца и строки из матрицы, соответствующих узлу короткого замыкания:
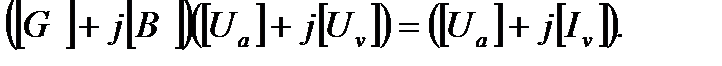(4.3)
Выполнив перемножение матриц в левой части, получим систему 2(n-2) уравнений с вещественными коэффициентами относительно активных и реактивных составляющих узловых напряжений:
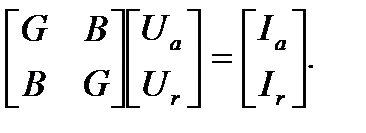(4.4)
В программе W_ТКЗ узловые уравнения (4.4) формируются в виде:
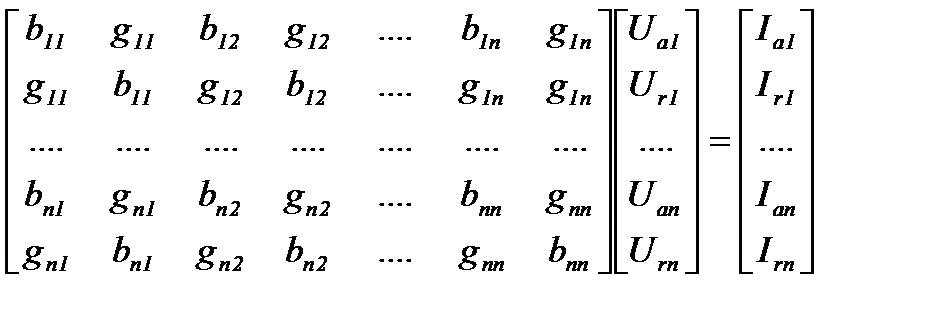, (4.5)
т.е. попарно для активных и реактивных составляющих токов каждого узла. При этом элементами матрицы являются блоки второго порядка 2х2, и для решения узловых уравнений с матрицей, состоящей из унифицированных блоков, применяется та же процедура, что и на шаге расчета нормального режима.