Метод равномерного симплекса
2.1 Описание алгоритма
Суть метода заключается в исследовании целевой функции в вершинах некого "образца", построенного в пространстве вокруг "базовой" точки. Вершина, давшая наибольшее значение целевой функции отображается относительно двух других вершин и таким образом становится новой базовой точкой, вокруг которой строится новый образец и снова выполняется поиск. В случае двух переменных симплексом является равносторонний треугольник, в трёхмерном пространстве - тетраэдр.
Работа алгоритма начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой точке. Затем определяется вершина с максимальным значением целевой функции и проектируется через центр тяжести оставшихся вершин в новую точку.
Процедура продолжается до тех пор, пока не будет накрыта точка минимума. В этом случае можно пользоваться следующими правилами:
1) Если вершина с максимальным значением целевой функции построена на предыдущем шаге, то отбрасывается вершина со следующим по величине значением целевой функции.
2) Если вокруг одной из вершин начинается циклическое движение, то необходимо уменьшить размеры симплекса.
Поиск заканчивается тогда, когда размеры симплекса или разность значений целевой функции становятся достаточно малыми.
При заданной начальной точке  и масштабном множителе
и масштабном множителе 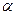 , координаты остальных
, координаты остальных  вершин симплекса в
вершин симплекса в  - мерном пространстве вычисляются по формуле:
- мерном пространстве вычисляются по формуле:
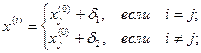
Приращения 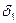 и
и  определяется по формулам:
определяется по формулам:

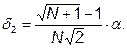
Величина 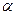 выбирается исследователем, исходя из характеристики решаемой задачи. При
выбирается исследователем, исходя из характеристики решаемой задачи. При 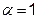 ребро симплекса имеет единичную длину.
ребро симплекса имеет единичную длину.
Вычисление центра тяжести:
Если 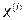 - точка, подлежащая отражению, то координаты центра тяжести определяются по формуле:
- точка, подлежащая отражению, то координаты центра тяжести определяются по формуле:
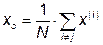
Координаты новой вершины удовлетворяют уравнению:
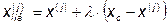
Для того чтобы симплекс обладал свойством регулярности, отображение должно быть симметричным, т.е. 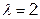
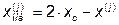
Если некоторая вершина симплекса не исключается на протяжении нескольких итераций, то необходимо уменьшить размер симплекса и построить новый симплекс, выбрав в качестве базовой точку с минимальным значением целевой функции.
2.2 Нахождение минимума целевой функции методом равномерного симплекса
Исходные данные:

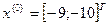 - начальная точка
- начальная точка
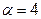 - масштабный множитель
- масштабный множитель
Минимизируем целевую функцию до первого уменьшения размера симплекса
Пусть масштабный множитель - 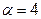
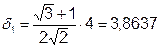
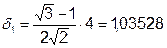
1-я итерация:
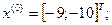
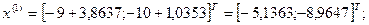
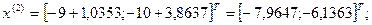
 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
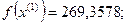

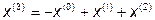
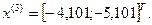
2-я итерация:
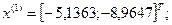
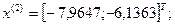
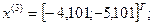
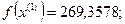
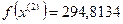 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
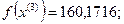
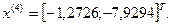
3-я итерация:
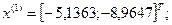
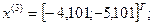
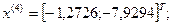
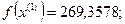 - максимально, следовательно, заменяем
- максимально, следовательно, заменяем
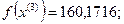
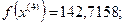
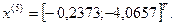
4-я итерация:
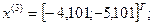
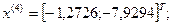
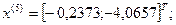
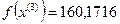 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
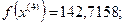
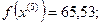
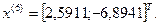
5-я итерация:
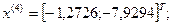
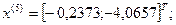
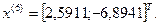
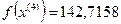 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
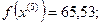
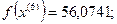
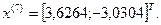
6-я итерация:
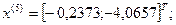
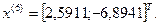
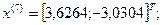
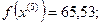 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
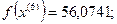
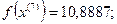
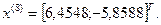
7-я итерация:
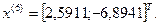
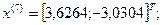
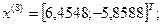
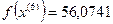 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
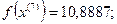
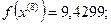
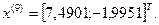
8-я итерация:
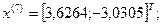
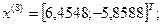

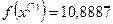 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
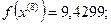
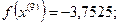
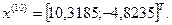
9-я итерация:
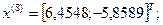

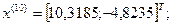
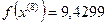 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
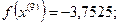
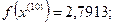
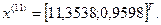
10-я итерация:

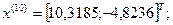
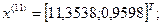
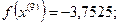
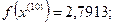
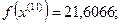
Так как наибольшее значение целевой функции соответствует 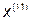 , которое получено на предыдущей итерации, отбрасываем
, которое получено на предыдущей итерации, отбрасываем 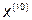 .
.
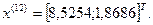
11-я итерация:

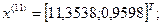
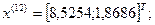
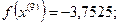
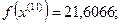
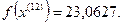
Так как наибольшее значение целевой функции соответствует 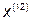 , которое получено на предыдущей итерации, отбрасываем
, которое получено на предыдущей итерации, отбрасываем 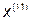 .
.
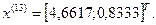
12-я итерация:

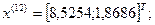
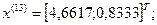
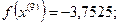
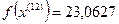 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
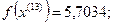

13-я итерация:

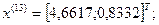
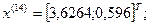
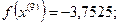
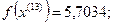
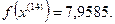
Так как наибольшее значение целевой функции соответствует  , которое получено на предыдущей итерации, отбрасываем
, которое получено на предыдущей итерации, отбрасываем 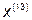 .
.
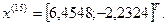
14-я итерация:

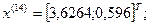
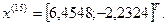
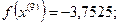
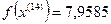 - максимально, следовательно, заменяем;
- максимально, следовательно, заменяем;
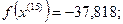
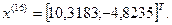
Симплекс сделал один оборот в области расположения точки 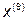 , то есть точку
, то есть точку 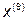 при заданных условиях можно считать точкой минимума целевой функции
при заданных условиях можно считать точкой минимума целевой функции  (для получения более точного решения необходимо уменьшить размер симплекса).
(для получения более точного решения необходимо уменьшить размер симплекса).
Таким образом, точка 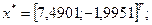 - точка минимума, значение функции в которой
- точка минимума, значение функции в которой 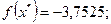 .
.
 Рисунок 2. Графическое пояснение метода равномерного симплекса
Рисунок 2. Графическое пояснение метода равномерного симплекса
Метод Хука-Дживса
3.1 Описание алгоритма
Процедура Хука-Дживса представляет собой комбинацию "исследующего" поиска с циклическим изменением переменных и ускоряющего поиска по найденному образцу. Исследующий поиск ориентирован на выявление направления вдоль "оврагов". Полученная в результате исследующего поиска информация используется затем в процессе поиска по образцу при движении по "оврагам".
Исследующий поиск.Для проведения исследующего поиска необходимо задать величину шага, которая может быть различна для разных координатных направлений, и изменяться в процессе поиска. Поиск начинается в некоторой исходной точке. Делается пробный шаг вдоль одного из координатных направлений. Если значение целевой функции в пробной точке меньше, чем в исходной, то шаг считается удачным. В противном случае возвращаются в исходную точку и делают шаг в противоположном направлении. После перебора всех  координат исследующий поиск заканчивается. Полученную в результате исследующего поиска точку называют базовой.
координат исследующий поиск заканчивается. Полученную в результате исследующего поиска точку называют базовой.
Поиск по образцу.Поиск по образцу в заключается в реализации единственного шага из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка определяется по формуле:
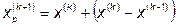
Как только движение по образцу не приводит к уменьшению целевой функции, точка  фиксируется в качестве временной базовой точки и выполняется исследующий поиск. При уменьшении значения целевой функции эта точка рассматривается как базовая точка. Если же исследующий поиск не дал результата, необходимо вернуться в предыдущую точку и провести исследующий поиск заново. Если такой поиск не приводит к успеху, то необходимо уменьшить величину шага. Поиск завершается, когда величина шага приращения становится достаточно малой.
фиксируется в качестве временной базовой точки и выполняется исследующий поиск. При уменьшении значения целевой функции эта точка рассматривается как базовая точка. Если же исследующий поиск не дал результата, необходимо вернуться в предыдущую точку и провести исследующий поиск заново. Если такой поиск не приводит к успеху, то необходимо уменьшить величину шага. Поиск завершается, когда величина шага приращения становится достаточно малой.
3.2 Алгоритм метода
Шаг 1. Задать:
1. Начальную точку  ;
;
2. Приращение 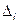 ,
, 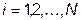 ;
;
3. Коэффициент уменьшения шага 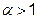 ;
;
4. Параметр окончания поиска 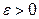 .
.
Шаг 2. Произвести исследующий поиск.
Шаг 3. Поиск удачный:
Да:
перейти к шагу 5;
Нет:
продолжить.
Шаг 4. Проверка на окончание поиска: 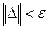 ?
?
Да:
прекратить поиск;
Нет:
уменьшить приращение по формуле: 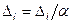 ,
, 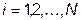 ;
;
Перейти к шагу 2.
Шаг 5. Провести поиск по образцу: 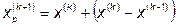
Шаг 6. Провести исследующий поиск, используя  в качестве базовой точки:
в качестве базовой точки: 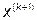 - полученная в результате точка
- полученная в результате точка
Шаг 7. Выполняется ли условие 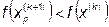 ?
?
Да:
продолжить 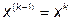 ;
; 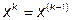 ;
;
перейти к шагу 5;
Нет:
перейти к шагу 4.
3.3 Нахождение минимума целевой функции методом Хука-Дживса.
Исходные данные:

 - начальная точка;
- начальная точка;
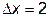 - векторная величина приращения;
- векторная величина приращения;
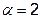 - коэффициент уменьшения шага.
- коэффициент уменьшения шага.
Минимизируем значение целевой функции до первого сокращения шага поиска
1. 

Исследующий поиск вокруг базовой точки  :
:
фиксируя 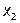 , даём приращение переменной
, даём приращение переменной  :
:
 ;
; 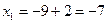 ;
; 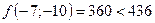 - поиск удачен;
- поиск удачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 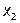 :
:
 ;
;  ;
; 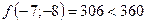 - поиск удачен;
- поиск удачен;
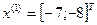
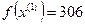
Так как поиск удачен, то переходим к поиску по образцу:
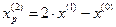
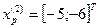
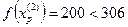
2. Исследующий поиск вокруг точки 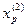 :
:
фиксируя 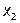 , даём приращение переменной
, даём приращение переменной  :
:
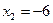 ;
; 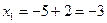 ;
; 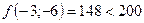 - поиск удачен;
- поиск удачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 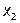 :
:
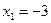 ;
; 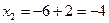 ;
; 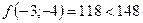 - поиск удачен;
- поиск удачен;
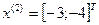
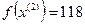
Так как поиск удачен, то переходим к поиску по образцу:
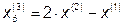
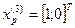
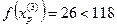
3. Исследующий поиск вокруг точки  :
:
фиксируя 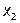 , даём приращение переменной
, даём приращение переменной  :
:
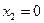 ;
; 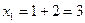 ;
; 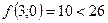 - поиск удачен;
- поиск удачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 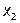 :
:
 ;
; 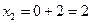 ;
; 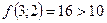 - поиск неудачен;
- поиск неудачен;
 ;
; 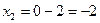 ;
; 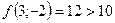 - поиск неудачен;
- поиск неудачен;

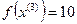
Так как поиск удачен, то переходим к поиску по образцу:
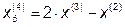
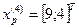
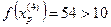
4.
Исследующий поиск вокруг базовой точки 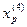 :
:
фиксируя 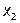 , даём приращение переменной
, даём приращение переменной  :
:
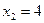 ;
; 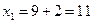 ;
; 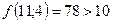 - поиск неудачен;
- поиск неудачен;
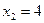 ;
; 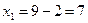 ;
; 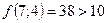 - поиск неудачен;
- поиск неудачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 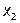 :
:
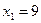 ;
; 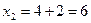 ;
; 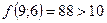 - поиск неудачен;
- поиск неудачен;
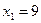 ;
; 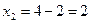 ;
; 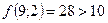 - поиск неудачен;
- поиск неудачен;
В результате исследующего поиска не было достигнуто уменьшение значения целевой функции, то есть значение шага (векторной величины приращения) уменьшить в 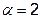 раз, до величины
раз, до величины 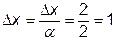 , затем необходимо произвести исследующий поиск вокруг точки
, затем необходимо произвести исследующий поиск вокруг точки 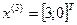 , используя новое значение приращения
, используя новое значение приращения 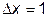 .
.
5. 
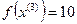
Исследующий поиск вокруг базовой точки 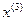 :
:
фиксируя 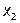 , даём приращение переменной
, даём приращение переменной  :
:
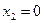 ;
; 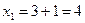 ;
; 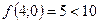 - поиск удачен;
- поиск удачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 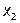 :
:
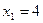 ;
; 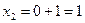 ;
; 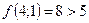 - поиск неудачен;
- поиск неудачен;
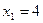 ;
; 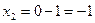 ;
;  - поиск удачен;
- поиск удачен;
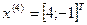
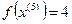
Так как поиск удачен, то переходим к поиску по образцу:
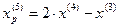
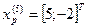
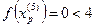
6.
Исследующий поиск вокруг точки 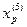 :
:
фиксируя 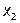 , даём приращение переменной
, даём приращение переменной  :
:
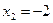 ;
; 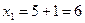 ;
; 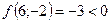 - поиск удачен;
- поиск удачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 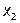 :
:
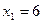 ;
; 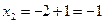 ;
; 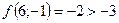 - поиск неудачен;
- поиск неудачен;
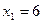 ;
; 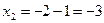 ;
; 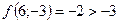 - поиск неудачен;
- поиск неудачен;
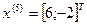
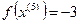
Так как поиск удачен, то переходим к поиску по образцу:
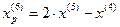
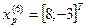
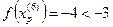
7.
Исследующий поиск вокруг точки 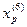 :
:
фиксируя 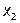 , даём приращение переменной
, даём приращение переменной  :
:
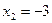 ;
; 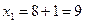 ;
;  - поиск неудачен;
- поиск неудачен;
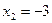 ;
; 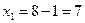 ;
;  - поиск неудачен;
- поиск неудачен;
фиксируя  , даём приращение переменной
, даём приращение переменной 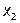 :
:
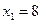 ;
; 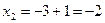 ;
; 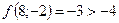 - поиск неудачен;
- поиск неудачен;
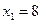 ;
; 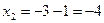 ;
; 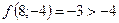 - поиск неудачен;
- поиск неудачен;
В результате исследующего поиска не было достигнуто уменьшение значения целевой функции, то есть значение шага (векторной величины приращения) уменьшить в 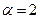 раз, до величины
раз, до величины 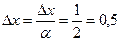 , затем необходимо произвести исследующий поиск вокруг точки
, затем необходимо произвести исследующий поиск вокруг точки 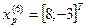 , используя новое значение приращения
, используя новое значение приращения 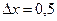 .
.
Итерации продолжаются, пока величина шага не укажет на окончание поиска в окрестности точки минимума.

Рисунок 3. Графическое пояснение метода Хука-Дживса
