Спектральный анализ непериодических сигналов

Свойства непериодического сигнала в частотной области характеризует функция спектральной плотности 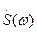, имеющая смысл комплексной амплитуды гармоники, приходящийся на 1Гц в бесконечно узкой полосе частот, содержащей рассматриваемую частоту ω. Функция 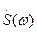имеет размерность

[единица напряжения (тока)/единица частоты]

и при известной функции s(t) может быть найдена с помощью прямого преобразования Фурье

(5.1)

Выражение (5.1) можно использовать при исследовании сигналов, функция s(t) которых удовлетворяет условию абсолютной интегрируемости (5.2).

(5.2)

После получения функции 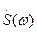, которая обычно является комплексной, с целью более наглядного представления спектральных характеристик сигнала строят графики зависимостей S(ω)=│ 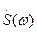│ (амплитудный спектр), а в некоторых случаях

и ψ(ω)=arg[ 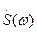]-фазовый спектр.

Поскольку отдельные составляющие в спектре непериодического сигнала смещены на бесконечно малую величину dω, спектр непериодического сигнала называют сплошным.

По известной спектральной функции 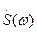можно найти (восстановить) временную зависимость с помощью обратного преобразования Фурье

(5.3)

При решении задач по спектральному анализу непериодических сигналов бывает полезно использовать ряд свойств преобразований Фурье. И в частности:

- свойство линейности: если сигналу s₁(t) отвечает спектральная плотность 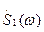, сигналу s₂(t) - спектральная плотность 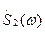ω), то сигнал s(t)=s₁(t)±s₂(t) будет иметь спектральную плотность = ± ,

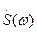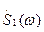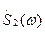- свойство запаздывания: если сигнал s(t) имеет спектральную функцию 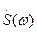. то сигнал s₁(t), отличающийся от s(t) только смещением во времени s₁(t)=s(t-τ), имеет спектральную функцию 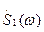= 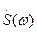e^-iωτ. При этом амплитудные спектры сигналов s(t) и s₁(t) совпадут, а их фазовые спектры будут отличаться на ωτ.

Например, трапецеидальный импульс (рис.5.26) можно представить в виде суммы четырех линейно изменяющихся напряжений (рис.5.27)

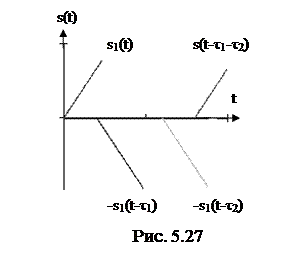
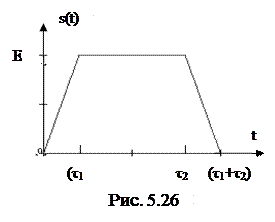
Тогда достаточно найти спектральную плотность сигнала s₁(t) функцию .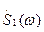

. При этом спектральная плотность сигнала s(t) - функция 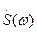запишется так

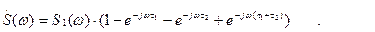
Для нахождения модуля полученной выше функции 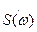полезно вынести из скобки общий множитель .

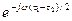2.2. Расчет частотных характеристик электрических цепей, содержащих операционные усилители

Идеальным операционным усилителем (ОУ) называется идеальный источник напряжения, управляемый напряжением (ИНУН), с бесконечно большим коэффициентом усиления k → ∞. Входные токи ОУ равны нулю. Выходное сопротивление идеального операционного усилителя также равно нулю.

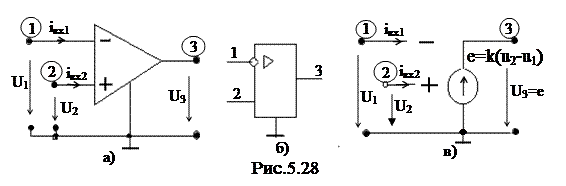На рис. 5.28 показано условное графическое изображение идеального (а), реального (б) ОУ и схема замещения идеального усилителя(в).

Усилитель имеет две пары входных полюсов (1 – 0) и (2 – 0) и выходные полюса (3 – 0). Особенность ОУ состоит в том, что выходное напряжение U₃ пропорционально разности напряжений на входных зажимах U_1, U₂, а входные токи I_1вх1 и I_вх2 равны нулю.

U₃ =k∙(U₂ – U₁); I_1вх1 = 0; I_вх2 = 0, (5.4)

где k – коэффициент усиления.

Уравнения (7) называют основными уравнениями ОУ.

Схема замещения идеального ОУ (рис. 5.28 в) представлена идеальным управляемым источником напряжения e = ƒ(U₁, U₂) = k·(U₂ – U₁). Если соединить между собой входные зажимы (2 – 0), т.е. U₂ = 0, то, как следует из выражений (5.4), ОУ ведет себя как инвертирующий усилитель т.е U₃ = –k∙U₁ – выходное напряжение отличается от входного по фазе на 180⁰. При соединении между собой зажимов (1 – 0) т.е. U₁ = 0, ОУ ведет себя как неинвертирующий усилитель U₃ = k·U₂. В связи с этим, зажимы (1 – 0) называются инвертирующим входом, а зажимы (2 – 0) – неинвертирующим входом. На графических изображениях ОУ инвертирующий вход обозначен знаком «–» или кружком, неинвертирующий «+»

При анализе схем, содержащих ОУ, следует учитывать основное свойство ОУ, вытекающее из (4):

– при конечном значении выходного напряжения U_вых = U₃ и бесконечно большом коэффициенте усиления k разность (U_вх2 – U_вх1) должна стремится к нулю, т.е. зажимы 1 и 2 должны иметь одинаковый потенциал φ_вх1 = φ_вх2 = U_вх1 = U_вх2. Это допущение, а также учет того, что входные токи ОУ равны нулю и выходное сопротивление также равно нулю, позволяют существенно упростить анализ цепей с ОУ.

В некоторых случаях один из входов ОУ бывает соединен с базисным узлом, например U₂ = 0. Тогда U₁ = U₂ = 0.

Расчет цепей с ОУ можно проводить любым методом анализа, однако результаты расчета с учетом сформулированного свойства ОУ получаются проще при использовании метода узловых напряжений. Методика составления системы уравнений для цепи, содержащей идеальный ОУ, методом узловых напряжений при этом может быть такой.

1. Подключить к входу цепи источник сигнала в виде идеального источника напряжения или тока. Вариант с поключением на вход схемы идеального источника напряжения предпочтительнее, так как узел, к которому он подключен, станет зависимым и уравнение для него можно не составлять.

2. Пронумеровать узлы схемы, в т.ч. входы и выходы ОУ. За базисный узел всей схемы принять базисный узел ОУ. Можно не прибегать к схеме замещения ОУ, а работать с исходной схемой цепи.

3. Записать систему уравнений по методу узловых потенциалов. Уравнения для узлов, соответствующих выходам операционных усилителей, не составлять.

4. Вычислить необходимые узловые напряжения схемы и определить операторный коэффициент передачи цепи.

Рассмотрим методику формирования узловых уравнений цепи, содержащей ОУ, при решении конкретной задачи.

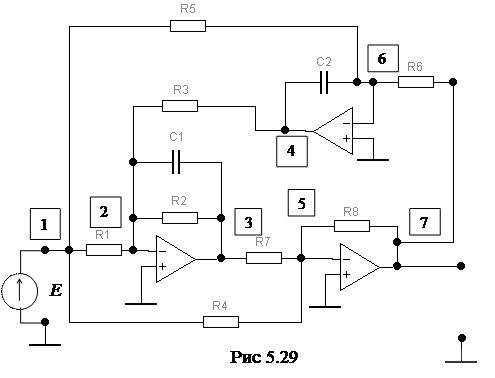
Пример: Найти операторный коэффициент передачи по напряжению цепи, схема которой изображена на рис. 5.29.

Решение. Задачу решим методом узловых напряжений. Для этого включим на входе цепи идеальный источник тока E и пронумеруем узлы. Проводить замену изображения ОУ схемой замещения не будем.

Между третьим и базисным, четвертым и базисным, седьмым и базисным узлами включены идеальные источники напряжения (если обратиться к схеме замещения операционного усилителя - Рис. 5.28в). Поэтому узлы 3, 4 и 7 являются зависимыми, и для них уравнения по первому закону Кирхгофа не составляются. Узел 1 также зависимый, так как к нему подключен идеальный источник напряжение и U11=E.

Для остальных узлов получаем следующую систему уравнений:

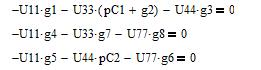(5.5)

Решая систему уравнений относительно U₁₁ и U₇₇, получим операторный коэффициент передачи по напряжению

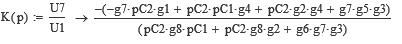(5.6)

2.3 Преобразование непериодического сигнала в линейной цепи

Существует два основных метода решения подобных задач: спектральный и временной.

При решении задачи спектральным методом используют частотные характеристики входного сигнала и цепи. Спектральную плотность отклика 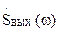можно найти по известным спектральной плотности воздействия 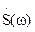и частотной характеристики цепи 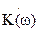с помощью выражения

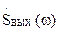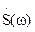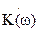= × (5.7)

Если нужно найти временную функцию отклика s_ВЫХ(t), то можно вычислить либо обратное преобразование Фурье от S_ВЫХ(w)

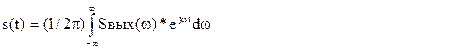
(5.8)

,

либо использовать операторный аналог этого выражения

s_ВЫХ(t)=L^-1[S(p)×K(p)], (5.9)

где L^-1 - символ обратного преобразования Лапласа,

S(p)-изображение воздействия

К(р)-операторный коэффициент передачи линейной цепи.

При решении задачи временным методом используют временные характеристики сигнала s(t) и цепи (либо импульсную характеристику g(t), либо переходную h(t)). При этом расчетное выражение может быть записано одним из следующих способов

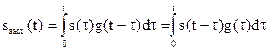(5.10)

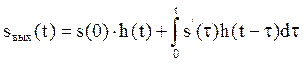
(5.11)

3. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ

3.1 Определить спектральную плотность одиночного прямоугольного импульса (рис.5.30). Построить амплитудный и фазовый спектры.

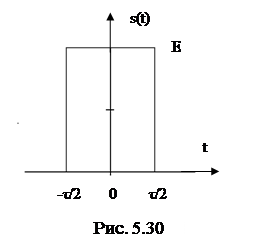
Решение.

Запишем функцию s(t):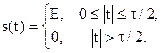

s(t) явно отвечает условию абсолютной интегрируемости. Поэтому прямо используем (1)

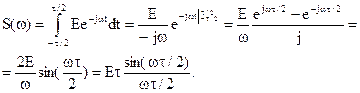(5.12)

Функция 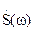получилась чисто вещественной. Однако при определенных значениях аргумента она принимает отрицательные значения. •Это необходимо учесть при построении спектров амплитуд и фаз.

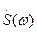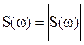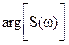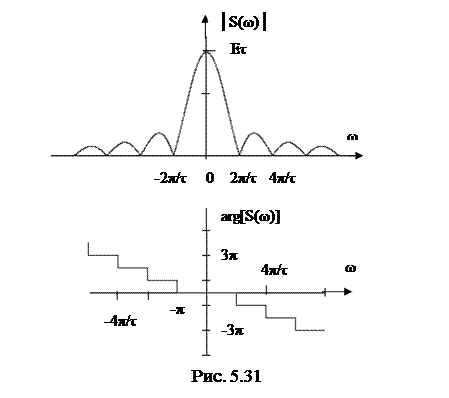
На тех участках оси абсцисс, где функция принимает отрицательные значения, мы будем рисовать . положительной, а будет равен нечетному числу 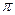. Спектры амплитуд и фаз одиночного прямоугольного импульса приведены на рис. 5.31.

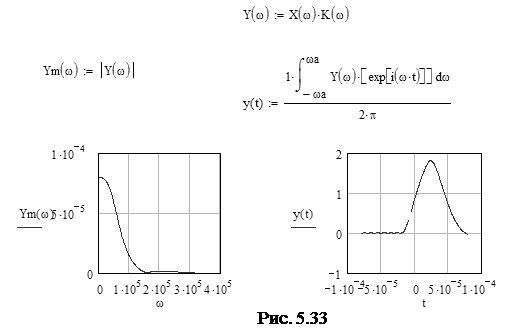
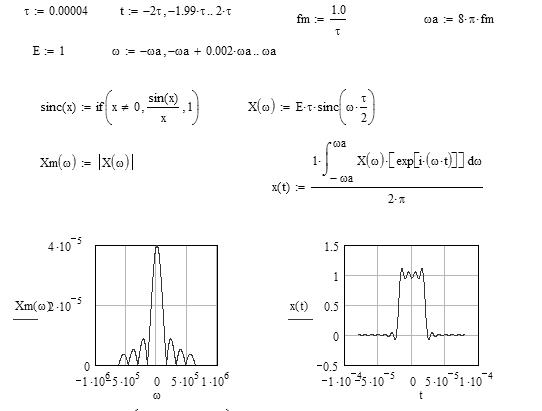
Для проверки правильности решения можно восстановить временную функцию по полученному выражению спектральной плотности с помощью программы “Sintnsp1”, текст которой приводится ниже

Определенное отличие формы восстановленного сигнала от исходного выражается в том, что у восстановленного сигнала фронты имеют конечную длительность, а вершина не плоская. Это связано с тем, что восстановление сигнала проводилось по ограниченной полосе частот –ω_а÷ω_а^. Чем шире эта полоса частот, тем ближе восстановленный сигнал к идеальному, и тем меньше среднеквадратическая погрешность “δ”, характеризующая различие между идеальным и восстановленным сигналами.

3.2 Предположим, что рассмотренный сигнал подается на активный RC фильтр, параметры и характеристики которого даны ниже

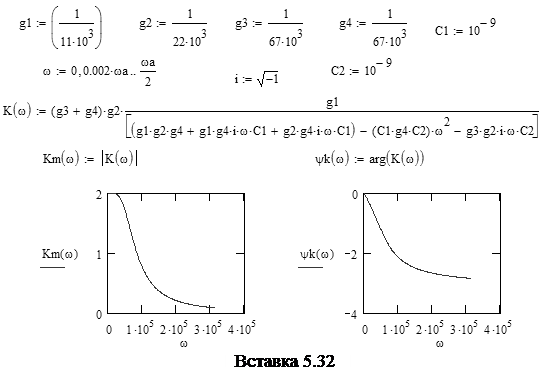
3.3 Определить временную функцию отклика, построить графики амплитудного спектра отклика и его временной функции можно с помощью выражения (5). Функции 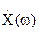, 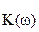уже известны. Достаточно подставить их в (5.5) и с помощью Mathcad рассчитать значения y(t) и построить ее график.

Все параметры функций 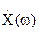, 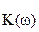должны быть заранее заданы. Внесите необходимые изменения в расположенный ниже пример. Будьте при этом внимательны и аккуратны. После завершения расчетов вы получите графики амплитудного спектра выходного сигнала и его временной функции.

Текст программы «Sintnsp1»

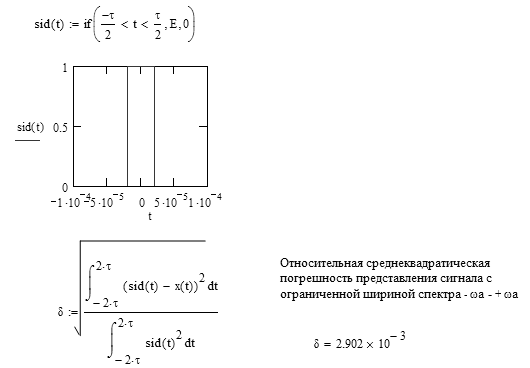
4. Литература

1. С. И. Баскаков. Радиотехнические цепи и сигналы, - М.:Высшая школа, 2000.

2. Бакалов В.П., Дмитриков В.Ф., Крук Б.Е. Основы теории цепей: Учебник для вузов; Под ред. В.П. Бакалова. 2-е изд., перераб. и доп. –М.: Радио и связь, 2000.

3. Козлов В.А, Базлов Е.Ф. "Радиотехнические цепи и сигналы". Задачи и упражнения к практическим занятиям. Казань, КАИ, 1999 г.

4. Гильмутдинов А.Х., Михайлов В.А., Султанов Э.И. Основы теории цепей. Казань, 1998.

5. Михайлов В.А., Султанов Э.И. Расчет частотных и переходных характеристик линейных активных цепей. Методическое пособие по курсовой работе. 2001. Кафедральное издание.

6. Михайлов В.А. Основы теории цепей: Учебное пособие по практическим занятиям. /Под ред. Е.Ф. Базлова. Казань: Изд-во Казан. гос. Техн. Ун-та, 2003.