Методы поиска экстремума функции, использующие расчет значений функции в вершинах многогранника
Симплекс метод
Одним из эффективных методов поиска оптимума функции многих переменных является симплекс метод Симплексом в пространстве n переменных называется выпуклый многогранник, имеющий n + 1 вершину. В пространстве двух переменных – это треугольник, в пространстве трех переменных – тетраэдр. В первоначальном симплексном методе использовался правильный симплекс, т.е. симплекс, все ребра которого равны между собой (например, равносторонний треугольник).
 |
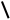
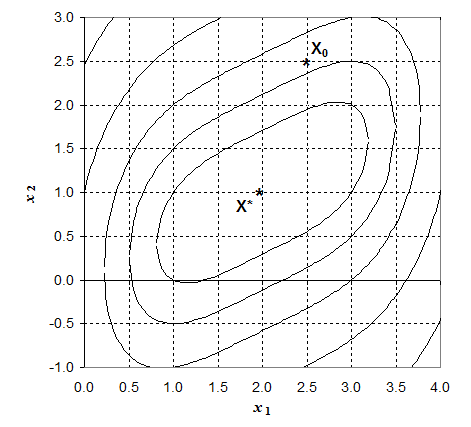Рис.2.3 Графическая иллюстрация поиска минимума функции методом Розенброка. Размещение правильного симплекса в пространстве n переменных может быть осуществлено различными путями. Часто используются два следующих способа.
1. Одна вершина симплекса помещается в начало координат, а остальные вершины располагаются так, чтобы ребра, выходящие из первой вершины, образовали одинаковые углы с соответствующими координатными осями. Координаты вершин симплекса в этом случае могут быть заданы следующей матрицей:
| Номера вершин | x1 | x2 | x3 | … | xn |
| … | |||||
| P | Q | Q | … | Q | |
| Q | P | Q | … | Q | |
| … | … | … | … | … | … |
| n + 1 | Q | Q | Q | … | P |
В этой матрице P = (1/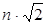 
) 
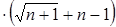; Q = (1/ 
) 
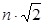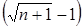
2. Центр симплекса помещается в начало координат, а (n+1) вершина на ось хn. Остальные вершины располагаются симметрично относительно координатных осей. В этом случае координаты вершин симплекса определяются матрицей:
| Номера вершин | x1 | x2 | x3 | … | xn |
| -R1 | -R2 | -R3 | … | -Rn | |
| V1 | -R2 | -R3 | … | -Rn | |
| V2 | -R3 | … | -Rn | ||
| … | … | … | … | … | … |
| n + 1 | … | Vn |
где Ri=1/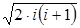 
; Vi=1/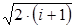 
И в первом, и во втором случаях формулы получены для симплекса, длина ребра которого равна единице. Для произвольной длины каждую формулу надо умножить на длину ребра l.
Идея симплекс метода заключается в следующем. Выбирается начальный симплекс (А-В-С) и в его вершинах рассчитываются значения целевой функции f(A), f(В), f(C). Из этих значений находится “наихудшая” точка: при поиске минимума функции эта та точка, в которой функция принимает наибольшее значение. Например, точка А. Через центр противолежащей грани (в данном случае это сторона В-С) строится новая вершина симплекса А', симметричная А. В результате получается симплекс А-В-А', причем значения целевой функции в двух его вершинах уже известны. Поэтому вычисляется значение функции в точке А' и среди всех вершин ищется вершина с “наихудшим” значением. Эта вершина (например С) снова отображается через центр противолежащей грани (сторона В-А') и вся процедура повторяется. При приближении к области экстремума возникает ситуация, когда значения целевой функции в полученной новой вершине снова оказывается «наихудшим». В простом симплексном методе обнаружение зацикливания является признаком того, что поиск экстремума необходимо закончить. Однако в этом случае точность нахождения экстремума будет целиком определяться размером симплекса. Если исходный симплекс имеет большие размеры, то, как правило, мало вероятно, что в ходе поиска одна из вершин поиска попадет в экстремум. Если же взять исходный симплекс с малой длиной ребра, то в этом случае резко возрастает количество вычислений целевой функции. Поэтому в применяемых модификациях данного метода при обнаружении зацикливания уменьшают размеры исходного симплекса. В окрестности экстремума процедура уменьшения размеров симплекса будет многократно повторяться, и в результате симплекс будет постоянно уменьшаться, стягиваясь в точке. Как только размер симплекса станет меньше выбранной точности поиска, процесс оптимизации закончится.