Компрессия данных. Метод Huffman-а
Классифкация алгоритмов компрессии данных.
Неискажающие (loseless) методы сжатия гарантируют, что декодированные данные будут в точности совпадать с исходными;
Искажающие (lossy) методы сжатия (называемые также методами сжатия с потерями) могут искажать исходные данные, например за счет удаления несущественной части данных, после чего полное восстановление невозможно.
Первый тип сжатия применяют, когда данные важно восстановить после сжатия в неискаженном виде, это важно для текстов, числовых данных и т. п. Полностью обратимое сжатие, по определению, ничего не удаляет из исходных данных. Сжатие достигается только за счет иного, более экономичного, представления данных.
Второй тип сжатия применяют, в основном, для видео изображений и звука. За счет потерь может быть достигнута более высокая степень сжатия. В этом случае потери при сжатии означают несущественное искажение изображения (звука) которые не препятствуют нормальному восприятию, но при сличении оригинала и восстановленной после сжатия копии могут быть замечены.
Компрессия данных. Метод Running и его модификации.
Это самый простой из методов упаковки информации. В исходной строке (сообщении) отыскиваются достаточно длинные серии следующих подряд друг за другом одинаковых символов, которые затем заменяются на более короткую комбинацию:
Алфавит = {A…Z} (26 символов)
Message = ”ABBBCCCCCCCDEFG” (15 символов)
Code_message = ”ABBB Х1 Х2 Х3 DEFG”
Х1 – специальный символ-метка, например, отсутствующий в исходной строке (M), по которому декодировщик узнает, что в этом месте нужно сделать обратную замену.
Х2 – сам тиражируемый символ (C).
Х3 – счетчик повторов (должен быть задан символами того же алфавита, в данном примере длина серии ССССССС равна 7, используем 7-й символ алфавита abcdefG) Получается, что при наилучшем раскладе удастся сжать 26 символов до 3.
Code_message = ”ABBB M C G DEFG”
Осталось только передать, какой символ выступает в роли метки. Проще всего добавить его на первое место в сообщении:
Code_message = ”MABBB M C G DEFG” (12 символов)
Ratio = 12/15 *100% = 80% (всегда считаем выгоду)
Компрессия данных. Метод LZW.
История этого алгоритма начинается с опубликования в мае 1977 г. Дж. Зивом (Jacob Ziv) и А. Лемпелем (Abraham Lempel) статьи в журнале "Информационные теории" под названием "IEEE Trans". В последствии этот алгоритм был доработан Терри А. Велчем (Terry Archer Welch) и в окончательном варианте отражен в статье "IEEE Compute" в июне 1984 . В этой статье описывались подробности алгоритма и некоторые общие проблемы с которыми можно столкнуться при его реализации. Позже этот алгоритм получил название - LZW (Lempel - Ziv - Welch).
Алгоритм LZW представляет собой алгоритм кодирования последовательностей неодинаковых символов.
M = "Класс TSuperCollection был порожден от TCollection" (50 символов)
Алфавит явно расширен = {а…яА…Яa…zA…Z…}
В сообщении обнаружен повтор. Закодируем его по схожему принципу:
C = "Класс TSuperCollection был порожден от T Х1 Х2 Х3" (50 символов)
Х2 – в этот раз данное поле содержит указатель на начало оригинальной серии
(13-я позиция = символ л)
C = "MКласс TSuperCollection был порожден от T M л и" (44 символа)
Ratio = 44/50 *100% = 88%
Очевидным преимуществом алгоритма является то, что нет необходимости включать таблицу кодировки в сжатый файл (самообучающийся алгоритм). Другой важной особенностью является то, что сжатие по алгоритму LZW является однопроходной операцией.
При компьютерной реализации обычно генерируется таблица замен для всех комбинаций из 3,4,5 и т.д. найденных последовательностей.
Компрессия данных. Метод RLE – класса в двоичной системе. Оптимизация.
Компрессия данных. Метод Huffman-а.
Первоначально, в передаваемом сообщении производится подсчет количества вхождений каждого из символов. На втором шаге происходит построение дерева путем попарного объединения вершин, из которого формируется словарь замен.
Алфавит = {00h…FFh} (256 символов – ASCII)
Message = { A=10 ; B=40 ; C=30 ; D=20 } (длина = 100 символов)
В задачах исходное сообщение может задаваться уже в виде набора символов и подсчитанных для них количеств вхождений. Тогда производить компрессию и записывать Code_message не нужно, достаточно лишь подсчитать Ratio.
Начинаем строить дерево Хаффмана: на каждом шаге ищем 2 свободные вершины, образующие наименьшую суммарную частоту – из них формируем новый узел.
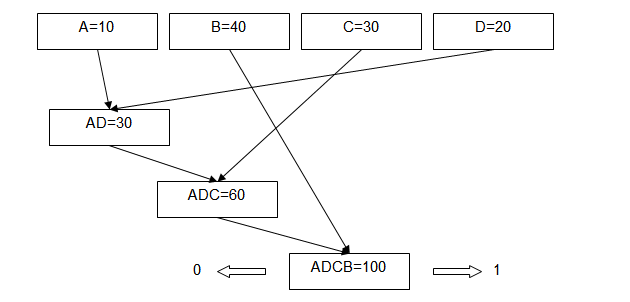
В результате все начальные вершины сходятся к «корню» дерева с суммой 100.
Теперь нужно для каждой начальной вершины закодировать «обратный путь»: начиная от корня, каждый поворот соответствует одному биту: 0 или 1.
A = { влево - влево - влево } = 000 ç СЛОВАРЬ
B = { вправо } = 1
C = { влево - вправо } = 01
D = { влево - влево - вправо } = 001
Поскольку у дерева нет «висящих» ветвей, код получается полным.
Расчет компрессии:

