Пример решения задания 1
ПРИМЕРЫ ЗАДАНИЙ НА АУДИТОРНУЮ КОНТРОЛЬНУЮ РАБОТУ
Задания 1 по теме "Позиционные системы счисления. Арифметические операции"
Выполните следующие действия
1. Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления, используя соответствующие правила перевода:
а) 666(10); б) 1997,715(10) .
2. Перевести данное число в десятичную систему счисления:
а) 1100111011(2); б) 100000110,10101(2); в) 257,125(8); г) 41A,6(16).
3. Перевести данное число в восьмеричную систему счисления:
а)А5Е16; б) 41Е,6(16).
4. Перевести данное число в шестнадцатеричную систему счисления:
а) 32718; б) 1724(8).
5. Выполнить сложение:
а) 10000011(2)+1000011(2); б) 110010,101(2)+1011010011,01(2).
6. Выполнить вычитание:
а) 100111001(2)-110110(2); б) 1101111011,01(2)-101000010,0111(2).
7. Выполнить умножение:
а) 11101,11(2)´ 1001,11(2).
Примечание. В заданиях 5 – 7 проверять правильность вычислений переводом исходных данных и результатов в десятичную систему счисления.
ПРИМЕР РЕШЕНИЯ ЗАДАНИЯ 1
А) Требуется перевести число 1997,71510 в шестнадцатеричную систему счисления, оставив 4 знака после запятой.
Решение.
При решении данной задачи используются следующие правила.
Правило 1. Смешанные числа десятичной системы счисления переводятся в два приема: отдельно целая часть по своему правилу и отдельно дробная часть по своему правилу. Затем записывается общий результат, у которого дробная часть отделяется запятой.
Правило 2. Для перевода целого десятичного числа А в систему счисления с основанием q, необходимо число А делить на основание q до получения целого остатка меньшего q. Полученное частное следует снова делить на q до получения целого остатка меньшего q и т.д., до тех пор, пока последнее частное не будет меньше q. Тогда десятичное число А в системе счисления с основанием q следует записать в виде последовательности остатков деления в порядке обратном их получению, причем старший разряд дает последнее частное.
Правило 3. Для перевода десятичной дроби в систему счисления с основанием q, следует умножить это число на основание q. Целая часть произведения будет первой цифрой числа в системе счисления с основанием q. Затем, отбросив целую часть, снова умножить на основание q и т.д., до тех пор, пока не будет получено требуемое число разрядов в новой системе счисления или пока перевод не закончится.
1. Используя правило 2, переведем целую часть числа

 _1997 16
_1997 16
 16 _124 16
16 _124 16


 _39 112 7
_39 112 7
 32 12=C
32 12=C
_77
 64
64
13=D 1997 10 = 7СD16
2. Используя правило 3, переведем дробную часть числа
| Х 0,715 16 В= Х 11,440 16 Х 7,040 16 Х 0,640 16 А=10,240 |
| 0,71510=0,В70А16 |
3. По правилу 1 1997,71510 = 7СD,В70А16
Ответ: 7СD,В70А16
Б) Требуется перевести 257,125(8) в десятичную систему счисления.
Решение.
Для перевода в десятичную систему счисления следует использовать формулу:
Аq = anqn + an-1qn-1 + ... + a1q1 + a0q0 + a-1q-1 + a-2q-2 + ... + a -kq-k
где Аq - число, записанное в системе счисления с основанием q,
n+1 - количество разрядов целой части числа,
аi - цифры числа, причем 0 £ аi < q,
k - количество разрядов в дробной части числа.
257,258 = 2*82 + 5*81 + 7*80 + 2*8-1+5*8-2 = 128+40+7+0,25+0,06=175,3110
Ответ: 175,3110
В) Требуется перевести А5Е16 в восьмеричную систему счисления.
Чтобы перевести целое число из шестнадцатеричной системы счисления в восьмеричную систему, следует сначала это число перевести в двоичную систему счисления, а затем полученное двоичное число перевести в восьмеричную систему счисления, используя следующие правила.
Правило 1. Чтобы перевести целое число из шестнадцатеричной системы счисления в двоичную, следует для каждой шестнадцатеричной цифры отвести 4 двоичных разряда, а затем выполнить перевод шестнадцатеричных цифр в двоичные коды.
Правило 2. Для перевода целого числа из двоичной системы счисления в восьмеричную систему необходимо последовательность двоичных цифр разбить на группы по 3 разряда справа налево (на триады), а затем в каждой триаде двоичный код заменить восьмеричной цифрой.






 А5Е16 = 1010010111102 = 51368
А5Е16 = 1010010111102 = 51368
5 1 3 6
1010 0101 1110
Ответ: 51368
Г) Требуется перевести 32718 в шестнадцатеричную систему счисления.
Решение.
Чтобы перевести целое число из восьмеричной системы счисления в шестнадцатеричную систему, следует сначала это число перевести в двоичную систему счисления, а затем полученное двоичное число перевести в шестнадцатеричную систему счисления, используя следующие правила.
Правило 1. Чтобы перевести целое число из восьмеричной системы счисления в двоичную, следует для каждой восьмеричной цифры отвести 3 двоичных разряда, а затем выполнить перевод восьмеричных цифр в двоичные коды.
Правило 2. Для перевода целого числа из двоичной системы счисления в шестнадцатеричную систему необходимо последовательность двоичных цифр разбить на группы по 4 разряда справа налево (на тетрады), а затем в каждой тетраде двоичный код заменить шестнадцатеричной цифрой.




 32718 = 0110101110012 = 6В916
32718 = 0110101110012 = 6В916
6 В 9
011 010 111 001
Ответ: 6В916
Д) Требуется вычислить 11101,112´1001,112.
Решение.
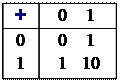
При решении данного примера следует использовать следующие таблицы сложения и умножения цифр.
 |  |
Х 11101,11
 1000,11
1000,11
+ 1110111
 1110111
1110111
100000100,0101
Ответ: 11101,112´1001,112=100000100,01012
