Размещения с повторениями

Пусть даны 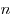различных видов предметов, которые можно разместить по 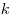различным местам, причем выбирать предметы можно с повторениями (т.е. можно выбрать несколько предметов одного вида). Такие выборки называются размещениями с повторениями, а их количество вычисляется по формуле: .

Сочетания с повторениями

Пусть имеются предметы 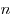различных видов предметов, и из них составляются наборы, содержащие 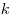элементов. Такие выборки называются сочетаниями с повторением. Их число обозначается .

Теорема:число сочетаний с повторениями может быть вычислено по формулам:

.

Случайные события.

Различают следующие виды случайных событий: достоверные, невозможные и случайные. События обозначаются большими латинскими буквами А, В, С,...,Z. Достоверное событие всегда происходит в результате наблюдения или испытания. Достоверное событие обозначается символом – W.

Невозможное событие никогда не происходит в результате наблюдения или испытания. Невозможное событие обозначается символом – Æ.

Пример. Если в корзине только персики, то достать из корзины персик является достоверным событием, а достать лимон является невозможным событием.

Случайное событие – это такое событие, которое в результате наблюдения или испытания может произойти, а может и не произойти.

Пример. Студент сдаёт экзамен. Экзамен сдан. Это событие случайное, так как студент мог и не сдать экзамен.

Кроме того, события могут быть совместными и несовместными, зависимыми или независимыми. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Примеры совместных событий: два стрелка стреляют по мишени, два спортсмена одновременно бегут. Случайные события А и В называются несовместными, если при данном испытании появление одного из них исключает появление другого события. Несовместные события: день и ночь, студент одновременно едет на занятие и сдаёт экзамен, число иррациональное и чётное.

Событие А называется независимым от события В, если вероятность появления события А не зависит от того произошло событие В или нет. Пример. Два студента одновременно сдают экзамен независимо друг от друга. Это событие совместное и независимое. Событие А называется зависимым от события В, если вероятность появления события А зависит от того произошло или не произошло событие В. Пример. Работник получит оплату труда в зависимости от качества её выполнения.

Равновозможные события – это такие события, которые имеют одинаковые возможности для их появления. Полная группа событий – это совокупность единственно возможных событий при данном испытании. Пример. Студент может сдать экзамен на любую оценку. В данном случае возможны следующие события: студент может сдать экзамен на 5, студент может сдать экзамен на 4, студент может сдать экзамен на 3. Эти события образуют полную группу.

Противоположные события. Два случайные события А и В называются противоположными, если они несовместны и образуют полную группу событий. Примеры: студент может сдать или не сдать экзамен, день и ночь.

Конкретный результат испытания называется элементарным событием. Совокупность всех возможных, различных, конкретных исходов испытаний называется множеством элементарных событий.

Сложным событием (исходом) называется произвольное подмножество множества элементарных событий. Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний произошло элементарное событие, принадлежащее сложному. Например, испытание – подбрасывание кубика. Элементарное событие – выпадение грани с числом «5». Сложное событие – выпадение грани с нечётным числом.

Вероятность является одним из основных понятий теории вероятностей. Существует несколько определений этого понятия. Одно из основных – это классическое определение. Это определение применимо в случаях, когда удается выделить полную группу несовместных и равновероятных событий, т.е. элементарных исходов.

Вероятностью события А называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех элементарных исходов:

.

Примеры непосредственного вычисления вероятностей.

Пример 5.

В группе 25 студентов. Из них 10 девушек и 15 юношей. Наугад выбирают одного студента. Найти вероятность того, что выберут юношу.

Решение. Искомая вероятность:

Классическое определение вероятности служит хорошей математической моделью тех случайных экспериментов, число исходов которых конечно, а сами исходы равновозможны и несовместны.