Основные идеи метода конечных элементов. Исследование прочности вагонных конструкций с помощью программного комплекса

Исследование прочности вагонных конструкций с помощью программного комплекса «ISCRA»

Учебное пособие

Санкт-Петербург

УДК 629.463.3:629.4.015

В учебном пособии изложены основные понятия метода конечных элементов (МКЭ) и реализующего его программного комплекса «ISCRA». Подробно описаны макропроцессоры и команды комплекса «ISCRA», приведены примеры его использования для расчета вагонных конструкций на прочность.

Пособие предназначено для студентов старших курсов специальности 0512 «Вагоностроение и вагонное хозяйство» и может быть использовано при подготовке бакалаврских и магистерских диссертаций и дипломном проектировании. Пособие представляет интерес для работников железнодорожного транспорта и научных сотрудников проектно-конструкторских бюро вагоностроительных заводов, выполняющих прочностные расчеты вагонных конструкций.

Введение

В процессе проектирования нового и модернизации существующего подвижного состава большое внимание уделяется оценке прочности вагонных конструкций с целью безусловного обеспечения требований безопасности при перевозке пассажиров и грузов железнодорожным транспортом.

Все современные методы проектирования базируются на использовании метода конечных элементов (МКЭ), позволяющего наиболее эффективно проводить оценку нагруженности отдельных элементов, узлов и всего вагона в целом, проводить локализацию зон концентрации напряжений и, в конечном итоге, улучшать технико-экономические показатели вагона. На базе МКЭ также может быть получена информация для прогнозирования долговечности вагонов и установления условий их безопасной эксплуатации.

Грамотный инженерный подход к использованию МКЭ позволяет существенно сократить трудозатраты на проектирование нового и модернизацию существующего подвижного состава.

Целью учебного пособия является изложение основ МКЭ и реализующего его программного комплекса, необходимых для практической работы по оценке прочности вагонных конструкций на современных ЭВМ, в т.ч. и объединенных в локальную сеть ПГУПС. Для этого теоретическое ознакомление с основами МКЭ и комплексом «ISCRA» иллюстрируется рядом примеров, позволяющих студентам самостоятельно начать работу в среде этого комплекса. Приобретенные навыки позволяет студентам в дальнейшем использовать комплекс «ISCRA» для подготовки бакалаврской и магистерской работы и дипломного проектирования.

Основные идеи метода конечных элементов

Метод конечных элементов (МКЭ) - это способ анализа поведения реальной конструкции при заданных нагрузках и перемещениях. Основной единицей представления конструкции в этом анализе является конечный элемент - геометрически упрощенное представление малой части физической конструкции. Модель конструкции создается при помощи конечных элементов.

МКЭ – один из основных методов решения задач строительной механики, механики деформируемого твердого тела, теплопроводности. Гидромеханики и др. Идея метода заключается в аппроксимации сплошной среды с бесконечным числом степеней свободы совокупностью простых элементов, имеющих конечное число степеней свободы и связанных между собой в узловых точках.

Для МКЭ характерны: широкий диапазон применимости, инвариантность по отношению к геометрии конструкции и механическим характеристикам материалов, простота учета взаимодействия конструкций с внешней средой (механические и температурные нагрузки, граничные условия и т.д.). высокая степень приспособленности к автоматизации всех этапов расчета. Популярность метода объясняется также простотой его физической интерпретации и очевидной связью с методами Ритца и перемещений, широко применяемыми в механике сплошных сред и строительной механике.

МКЭ во всех его различных формулировках предусматривает следующие основные этапы расчета: разбиение рассматриваемой области (тела) на конечные элементы; аппроксимацию зависимых переменных кусочно-полиномиальными функциями с неизвестными параметрами для каждого конечного элемента; подстановку аппроксимирующих функций в определяющие уравнения и их решение, дающее значение параметров, которые полностью определяют искомые функции внутри элемента через их значения в узловых точках.

С математической точки зрения МКЭ представляет собой обобщение метода Рэлея – Ритца – Галеркина, обеспечивающего минимизацию функционала потенциальной энергии путем отыскания линейной комбинации пробных функций:

,

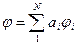где 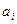– коэффициенты, определяемые из системы N алгебраических уравнений.

Основная проблема заключается в выборе пробных функций 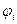, обеспечивающих простоту вычислений и достаточную точность. Особенность МКЭ в том, что эти функции принимают кусочно-полиномиальными, отличными от нуля в окрестности только одного узла, и коэффициенты 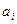имеют определенный физический смысл.

Примем здесь в качестве базового МКЭ в форме метода перемещений. В этом случае разрешающие уравнения получаем путем минимизации полной потенциальной энергии рассматриваемой системы. Выраженной через поле перемещений. Эти уравнения имеют простой физический смысл: они описывают равновесие узлов системы; искомые неизвестные являются компонентами узловых перемещений. Соответствующих весовыми коэффициентами. Используемым в методе Ритца. Расчет с помощью МКЭ в форме метода перемещений включает следующие этапы:

· разбиение конструкции на конечные элементы и подготовка топологической, геометрической и физической информации; установление факторов взаимодействия с окружающей средой;

· построение для выделенных конечных элементов соответствующих матриц (жесткости, масс, теплопроводности и др.) и векторов, определяющих зависимости между реакциями и перемещениями в узлах элемента;

· формирование разрешающей системы линейных алгебраических или дифференциально-алгебраических (в нестационарных задачах) уравнений;

· решение полученной системы уравнений и установление полей перемещений, внутренних силовых факторов, температуры и т.д.;

· обработку результирующей информации и ее анализ.

Перечисленные этапы поддаются четкой универсальной алгоритмизации, и их программная реализация не вызывает принципиальных затруднений при наличии библиотеки стандартных подпрограмм, реализующих второй и четвертый этапы расчета.