Метод квадратичной интерполяции – экстраполяции

Алгоритм ЗС-1

Начальный этап

(1) Выбрать погрешность расчёта e=10^-3¸10^-7. Получить начальный интервал методом Свенна.

(2) Вычислить стартовые точки l₁=a₁+0,382L₁, m₁=a₁+0,618L₁ (следует отметить, что золотые числа следует вычислять точно)

(3) Принять k=1 – счётчик числа итераций

Основной этап

Шаг 1.Сократить ТИЛ рассмотрением 2-х ситуаций:

(1) Если f(l)<f(m),то

a_k+1=a_k

b_k+1=m_k

m_k+1=l_k

l_k=a_k+1+0,382L_k+1

иначе

a_k+1=l_k

b_k+1=b_k

l_k+1=m_k

m_k=a_k+1+0,618L_k+1

(2) Положить k=k+1, L_k+1=|b_k+1-a_k+1|

Шаг 2. Проверить критерий окончания поиска: если |a_k+1-b_k+1|£e - остановиться – минимум найден. Точнее фиксируем аппроксимирующий минимум как . Иначе вернуться на шаг 1.

Алгоритм ЗС-2

Начальный этап

(4) Выбрать погрешность расчёта e=10^-3¸10^-7. Получить начальный интервал методом Свенна.

(5) Вычислить стартовые точки l₁=a₁+0,382L₁, m₁=a₁+0,618L₁ (следует отметить, что золотые числа следует вычислять точно)

(6) Принять k=1 – счётчик числа итераций

Основной этап

Шаг 1. Взять очередную пробную точку x₂=a_k+b_k-x₁, симметричную исходной и сократить ТИЛ рассмотрением 4-х возможных ситуаций:

(1) Если (x₁<x₂) и (f(x₁)<f(x₂)) то b=x₂;

(2) Если (x₁<x₂) и (f(x₁)>=f(x₂)) то a=x₁;

(3) Если (x₁>x₂) и (f(x₁)<f(x₂)) a=x₂;

(4) Если (x₁>x₂) и (f(x₁)>=f(x₂)) b=x₁;

Увеличить счётчик числа итераций k=k+1

Шаг 2. Проверить критерий окончания поиска: если |a_k+1-b_k+1|£e - остановиться – минимум найден. Точнее фиксируем аппроксимирующий минимум как . Иначе вернуться на шаг 1.

Метод Фибоначчи

Метод Фибоначчи является процедурой линейного поиска минимума унимодальной функции f(x) на замкнутом интервале [a, b], отличающейся от процедуры золотого сечения тем, что очередная пробная точка делит интервал локализации в отношении двух последовательных чисел Фибоначчи. Последовательность чисел Фибоначчи задаётся условиями F₀ = F₁ = 1, F_k+1 = F_k + F_k-1, k = 1,2,... Начальными членами последовательности будут 1, 1, 2, 3, 5, 8, 13,... Стратегия поиска Фибоначчи требует заранее указать n - число вычислений минимизируемой функции и e - константу различимости двух значений f(x). Рассмотрим один из возможных вариантов метода.

Алгоритм Фибоначчи-1

Начальный этап

(1) Задать константу e, начальный интервал [a₁, b₁], длину конечного интервала L_n и определить число n так, чтобы выполнялось условие F_n > (b₁ - a₁)/L_n.

(2) Взять две пробные точки l₁ = a₁ + (F_n-2/F_n)(b₁ - a₁) и m₁ = a₁ + (F_n-1/F_n)(b₁-a₁). Положить k = 1.

Основной этап

Шаг 1. Сократить текущий интервал локализации:

(1) Если f(l_k) < f(m_k), то положить a_k+1 = a_k, b_k+1 = m_k,m_k+1 =l_k и вычислить новую точку l_k+1 = a_k+1 + (F_n-k-2/F_n-k)L_k+1, где L_k+1 = b_k+1 - a_k+1; перейти на шаг 2.

(2) Если f(l_k)>> f(m_k),то положить a_k+1 =l_k, b_k+1 = b_k, l_k+1 = m_k и вычислить m_k+1 = a_k+1 + (F_n-k-1/F_n-k) L_k+1.

Шаг 2. Проверить критерий окончания поиска:

(1) Заменить k на k+1. (2) Если k = n - 1, перейти на шаг 3, иначе - на шаг 1.

Шаг 3. Найти аппроксимирующий минимум х^(*):

(1) Положить m_k = l_k + e.

(2) Если f(l_k) > f(m_k), то x^(*) = (l_k + b_k)/2. В противном случае - x^(*) = (a_k + m_k)/2.

Алгоритм Фибоначчи-2

Начальный этап

(1) Задать константу e, начальный интервал [a₁, b₁], длину конечного интервала L_n и определить число n так, чтобы выполнялось условие F_n > (b₁ - a₁)/L_n.

(2) Выбрать одну пробную точку . Положить

k = 1.

Основной этап

Шаг 1. Проверить критерий окончания поиска: если k=n, то остановиться и положить x*=x₂.

Шаг 2. Сократить текущий интервал локализации рассмотрением 4-х ситуаций, аналогично методу золотого сечения-2.

Метод линейной интерполяции (метод секущих)

Метод секущих предлагает заменить вторую производную f ''(x_k) в ньютоновской формуле её линейной аппроксимацией (f '(x_k)-f '(x_k-1))/(x_k-x_k-1).

Тем самым очередное приближение х_k+1 к стационарной точке х* задаётся формулой вида

x_k+1 = x_k - f '(x_k) * (x_k - x_k-1) / ( f '(x_k) - f '(x_k-1)).

Легко видеть, что х_k+1 - точка пересечения с осью абсцисс секущей прямой, проходящей через точки х_k и х_k-1.

В отличие от метода Ньютона метод секущих гарантирует сходимость точек {x_k} к стационарной точке х*, однако, сходимость метода достигается ценой потери быстродейсвия. Как правило, метод дихотомии оказывается эффективнее метода секущих, хотя последний и получен из более быстродействующей схемы.

Начальный этап. Пусть методом Свенна получен интервал неопределённости [a₁,b₁], границы которого удовлетворяют неравенству f'(a₁)f '(b₁) < 0. Задать e - погрешность вычисления минимума и принять k=1.

Основной этап

Шаг 1. Найти очередное приближение х_k+1 к минимуму х* и проверить условие окончания поиска:

(1) x_k+1 = b_k - f '(b_k)*(b_k - a_k)/(f '(b_k) - f '(a_k));

(2) если ½f '(x_k+1)½ << e, то остановиться.

Шаг 2. Уменьшить интервал поиска минимума:

(1) если f '(x_k+1) > 0, то a_k+1 = ak, b_k+1 = x_k+1, в противном случае принять a_k+1 = x_k+1, b_k+1 = b_k;

(2) положить k = k + 1 и перейти на шаг 1.

Метод средней точки (метод Больцано)

Данный метод является вариантом метода деления интервала пополам. Последовательные сокращения интервала неопределенности производятся на основе оценки производной минимизируемой функции в центре текущего интервала.

Начальный этап. Для запуска метода необходимо:

(1) задать [a₁,b₁]- начальный интервал локализации минимума, на границах которого знаки производных различны, т.е. f'¢(a₁)f'¢(b₁)<0; e - малое положительное число;

(2) положить к=1 и перейти к основному этапу.

Основной этап

Шаг 1. Взять пробную точку х_k в центре текущего интервала и проверить критерий окончания поиска: (1) x_k = (a_k + b_k)/2; (2) если ½f'¢(x_k)½ ≤ e и L_k= ½b_k - a_k½≤ e, то остановиться (х_k = х* -аппроксимирующий минимум).

Шаг 2. Сократить текущий интервал:

(1) Если f ¢(x_k) > 0, то положить a_k+1 = a_k и b_k+1 =x_k, в противном случае - a_k+1 =x_k, b_k+1 =b_k;

(2) заменить k на k+1 и вернуться на шаг 1.

Метод квадратичной интерполяции – экстраполяции

Данный метод относится к классу прямых методов, опирающихся на идею построения аппроксимирующего полинома второго порядка на основании информации о значениях функции в n+1 точке – узлах интерполяции.

Начальный этап

1. Выбрать произвольную точку x¹ÎRⁿ

2. Задаться величиной шага h=0.001

3. Определить погрешность

4. Положить счётчик числа итераций равным 1, а также b=x¹

Основной этап

Шаг 1. Вычислить f_i в 3-х точках: a, b и с – центральной (b) и двух соседних: a=b-h, c=b+h. Затем, по формуле

(1)

или

(2)

найти аппроксимирующий минимум d

Шаг 2. Проверить критерий близости 2-х точек b и d

и

Если оба условия выполняются – фиксируем аппроксимирующий минимум

и останавливаемся. Если оба критерия не выполняются, полагаем b=d и возвращаемся на шаг 1.

Метод Пауэлла

Метод Пауэлла является одним из самых популярных методов. Эффективен как и рассмотренный ранее алгоритм квадратичной интерполяции – экстраполяции, если начальная точка x¹Îd(x*).

Начальный этап

1. Выбрать ε₁, ε₂, h.

2. Взять 3 точки a, b, c на равных на равных интервалах. Предполагается, что сработал метод Свенна и получен интервал [a, b].

a=a;

c=b;

b=(a+c)/2;

Основной этап

1. Найти аппроксимирующий минимум на 1-й итерации по формуле:

на последующих итерациях по формуле:

2. Проверить критерии близости двух точек:

;

Если он выполняется, принять и остановиться.

Если не выполняется, то из 2-х точек b и d выбрать «лучшую» - в которой наименьшее значение функции, обозначить её как b, а 2 соседние с ней – a и c. Далее рассмотреть 4 ситуации аналогично ЗС-2.

3. Положить k=k+1 и вернуться на шаг 1.

Метод Давидона

Начальный этап

1. Выбрать ε, x⁰, p, α₁

2. Предполагается, что сработал метод Свенна и получен интервал [a, b].

Основной этап

1. Найти аппроксимирующий минимум, т.е. точку d по формулам:

2. Проверить КОП: если y`<sub>r</sub>≤ ε, то остановиться, х=a+α<sub>r</sub>p. Иначе: сократить ТИЛ: если y`_r <0, то [r,b], если y`_r >0, то [a,r].

Положить k=k+1 и вернуться на шаг 1.

Методы многомерной минимизации

Здесь имеет смысл упомянуть о поиске минимума функции многих переменных по направлению, так как этом используется во многих методах описываемых далее. Поиск минимума по направлению производится с использованием одномерных методов, т.е. сначала многомерная функция сводится к одномерной функции зависящей от смещения по заданному направлению из заданной точки, а потом для неё вызывается один из методов одномерной минимизации:

x – вектор от которого зависит функция

x0 – стартовая точка

p – направление

L – смещение по направлению

Метод Коши

Метод Коши относится к группе методов градиентного спуска. Градиентные методы – это методы, где на каждом шаге выбирается антиградиентное направление спуска.

Начальный этап

Выбрать x1, e, k.

Основной этап

Шаг 1

Шаг 2

(1) Найти L как результат минимизации функции по направлению p.

(2)

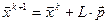
Шаг 3

(1) Вычислить новое значение градиента

(2) Проверить КОП: если , то , иначе на Шаг 1.