Аналоговые вычислительные устройства
Методы моделирования
Давно замечено, что различные физические процессы, происходящие в окружающем мире, описываются одинаковыми дифференциальными уравнениями. Поэтому, используя эту похожесть, можно исследовать мало изученные явления при помощи других, но описываемых идентичными математическими уравнениями.
Процесс изучения одного физического явления при помощи другого, описывающегося идентичными математическими уравнениями, называется моделированием.
Различают два типа моделирования: физическое и математическое. Если физика явлений в подлежащем изучению объекте и его модели одинаковы и процессы, протекающие в модели и объекте, описываются одинаковыми математическими и логическими зависимостями, то такое моделирование называется физическим. Метод физического моделирования имеет важное значение в том случае, когда исследуемый процесс не поддается математическому описанию. Основное достоинство физического моделирования заключается в том, что оно дает возможность наглядно видеть протекающие в модели процессы: сохраняются особенности проведения экспериментов в натуре, но существенно облегчается получение требуемых результатов, так как для модели выбирают удобные геометрические размеры и диапазоны изменения физических величин. Недостаток этого метода - необходимость строить дорогие модели при исследовании каждого нового объекта. Поэтому более удобным и универсальным является математическое моделирование.
Если физика явлений, протекающих в модели и в объекте, различна, то моделирование называется математическим, а само описание объекта - математической моделью. Главное преимущество математического моделирования перед физическим заключается в возможности исследования явлений природы, трудно поддающихся изучению, на хорошо изученных явлениях. Этот вид моделирования использует простые, дешевые и удобные в эксплуатации элементы. Массовое производство элементов электроники (резисторов, конденсаторов, диодов, транзисторов и т.д.) сделало их дешевыми и поэтому доступными для любой отрасли промышленности.
Основные достоинства математического метода моделирования позволили ему занять преимущественное положение при проведении научных исследований.
При использовании в качестве моделей электрических цепей каждой переменной величине исследуемого процесса соответствует определенная переменная величина электрической цепи. Например, для механических систем разработаны три типа электромеханических аналогий. В первой системе, предложенной Максвеллом, электрический заряд Q (табл. 2.1) соответствует механическому перемещению S, ток i электрической цепи - скорости v механической системы, а напряжение u - силе F. Во второй системе механическим параметрам - перемещению, скорости и силе - соответствуют электрические параметры: магнитный поток Ф, напряжение u и ток i ; в третьей системе - один электрический параметр - напряжение, измеренное в различных фиксированных точках электрической цепи. В связи с простотой измерения напряжений и возможностью моделирования различных процессов с помощью унифицированных элементов наиболее распространена третья система аналогий. На ее основе развито структурное моделирование.
Таблица 2.1. Cистемы электромеханических аналогий
| Механические параметры | Система электромеханических аналогий | ||
| I | II | III | |
| S | Q | Ф | u |
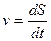 | 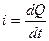 | 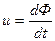 | u |
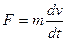 | 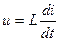 | 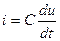 | u |
Помимо систем электромеханических аналогий, существуют электрогидравлические, электроакустические и другие виды аналогий. Электрические модели могут строится на основе прямых и непрямых аналогий.
При моделировании на основе прямых аналогий каждому физическому элементу процесса – оригинала соответствует аналогичный физический элемент процесса – модели, а взаимосвязь элементов оригинала аналогична взаимосвязи элементов модели. Таким образом строятся электрические модели для изучения физических процессов, протекающих непрерывно во времени и в пространстве координат. Примером пространственных процессов могут служить распространение теплоты, электромагнитных волн, жидкостей в простых средах и др. Так, для изучения процесса фильтрации воды в грунте можно использовать электропроводную бумагу, к которой приложено напряжение. Бумага представляет собой сплошную среду, являющуюся прямым аналогом исследуемого процесса. Контуры бумаги должны соответствовать границе земной поверхности, а приложенное напряжение перепаду высот. При этом распределение напряжений на проводящей бумаге будет подобным распределению напора в гидропроводящем грунте.
В моделях, построенных на основе непрямых аналогий, отсутствует прямая физическая связь между элементами, характеризующими изучаемое явление, и операционными блоками, из которых построена модель.
Изучение процесса моделирования показало, что идентичность двух математических зависимостей модели и изучаемого объекта не обеспечивает абсолютной аналогичности двух процессов. Для того, чтобы иметь возможность на модели производить изучение процессов, протекающих в объекте, необходимо соблюдать так называемые критерии подобия. Таким образом, при моделировании, например, уравнения
F=mdv/dt
нельзя просто сравнивать аналогичные ему по форме написания уравнения электрических цепей
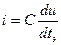 или
или 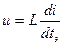 ,
,
где tэ - время протекания процесса в электрической цепи.
Необходимо при анализе соблюдать критерий их подобия. Действительно, сравнивать механическую силу F и силу тока i, массу m и емкость конденсатора С, скорость перемещения и напряжение не имеет никакого смысла. Для устранения этой трудности нужно оба сравниваемых уравнения выразить в безразмерных переменных величинах. С этой целью каждую переменную величину представим в виде произведения двух сомножителей - постоянного размерного и переменного безразмерного:
F=FpFб; m=mpmб; v=vpvб; t=tptб; i=ipiб; C=CpCб; u=upuб; tэ=tэ.р.tэ.б..
Подставляя эти значения в исходные уравнения и сгруппировав размерные параметры, получим:
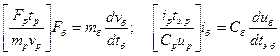 . (2.1.)
. (2.1.)
Оба уравнения имеют одинаковую форму написания и выражены в безразмерных величинах, что дает возможность их сравнивать. Очевидно, что уравнения тождественные друг другу, если их коэффициенты, заключенные в квадратные скобки, равны между собой, т.е.:
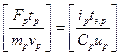 . (2.2.)
. (2.2.)
Это равенство называется критерием подобия для исходных уравнений. Оно позволяет определить параметры электрической модели по исходному уравнению объекта. Время протекания процесса в электрической цепи tэ в общем случае не равно времени протекания процесса t в исследуемом объекте, т.е. tэ¹t. Его выбирает оператор из условия удобства наблюдения за процессом. Если процессы в объекте протекают быстрее, чем оператор может их оценить, то время tэ протекания процесса в модели берут большим, чем время t протекания процесса в объекте, т.е. tэ>t. Если процесс протекает медленно, то для сокращения времени исследования время tэ выбирают меньшим времени t, т.е. tэ<t.
2.2.Методы построения аналоговых вычислительных
Устройств
Аналоговые вычислительные устройства (АВУ) в основном применяют для решения дифференциальных (обыкновенных или в частных производных), алгебраических и некоторых других видов уравнений. Для исследования обыкновенных дифференциальных уравнений АВУ строится по матричному или структурному методу.
Матричный метод. Он предусматривает жесткую коммутацию между функциональными блоками. Его используют обычно в специализированных машинах.
Структурный метод - это набор отдельных функциональных блоков, выполняющих различные математические операции (сложение, умножение, интегрирование, дифференцирование и т.д.). Шнуровая коммутация этих блоков дает возможность моделировать разнообразные дифференциальные уравнения, имеющие сильно отличающуюся друг от друга структуру решения. Такая универсальность обусловливает большое распространение АВУ, построенных по структурному методу.
Метод электрических сеток используется при решении задач, описываемых уравнениями в частных производных (исследование нефтегазоносных слоев, теплопроводности, блуждающих токов и многих других задач), решается на АВУ, построенные по методам электрических сеток или сплошных сред. Метод основан на использовании электрических сеток, имеющих сосредоточенные параметры. При моделировании дифференциальные уравнения предварительно преобразуются в систему линейных алгебраических уравнений методом конечных разностей. Этот метод достаточно универсален, широко применяется при проведении исследований и является основой построения ряда сеточных АВУ.
Метод сплошных сред. Метод основан на моделировании электрических явлений в сплошной проводящей среде. Он сравнительно точен, прост в эксплуатации, но ограничивается краевыми задачами математической физики, сводящимися в основном к уравнениям Лапласа. Реализация метода осуществляется с использованием электролитических ванн или электропроводной бумаги.
Особое место занимают гибридные вычислительные машины, которые перерабатывают цифровую информацию с помощью методов, используемых при построении АВУ.
