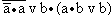Формы логических функций и их использование для синтеза логических схем
Запишем в форме логического выражения составное высказывание
(2*2=5 или 2*2=4) и (2*2 ≠ 5 или 2*2 ≠ 4)
(А или В) и (А или В)
(AvB)&(AvB)
Теперь выполняем логические операции, причем в строго определенном порядке: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
Подставим в логическое выражение значения логических переменных и получим значение логической функции:
F = (AvB)&(AvB) = (0v1) & (1v0) = 1&1 = 1
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы: Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы. Если А и В — формулы, то отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция между А и В — формулы. Никаких других формул в алгебре логики нет.
В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B) → C.
Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
Если две формулы А и В одновременно принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом "" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Определите истинность составного высказывания: (A&B)&(CvD).
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
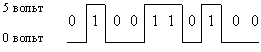В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.
Алгоритм построения таблицы истинности:
1) подсчитать количество переменных n в логическом выражении;
2) определить число строк в таблице, которое равно m = 2n;
3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
5) заполнить столбцы входных переменных наборами значений;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции.
Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1. Определите с помощью таблиц истинности, является ли формула тождественно истинна или тождественно ложна: 