Дискретизация сигналов при вводе в ЭВМ

При вводе информации в ЭВМ ее необходимо преобразовать в дискретный сигнал - код.

Описанный выше порядок показывает, что в общем виде сигнал может быть представлен во временных и пространственных координатах, кроме этого могут быть и другие параметры.

Например, для сигнала, представляющего информацию об изображении можно записать следующую математическую модель:

A = A (x, y, z, t, l),

где функция А описывает распределение амплитуды электромагнитных колебаний в зависимости от значений пространственных координат - x, y, z, времени - t и длины волны l, которая определяет спектр измерения в данной точке, т.е. цвет изображения.

Частным случаем такой модели является плоское, черно-белое изображение, описываемое моделью А = А (x,y), где функция А описывает распределение на плоскости яркости (световой интенсивности) изображения. Примером таких источников сигналов являются рентгенограммы, получаемые в медицине или при диагностике сварных швов.

Бинарные изображения передаются в ЭВМ при снятии информации с машинописных и рукописных шрифтов, чертежно-графической информации и т.п.

В более общем случае функция А (x,y) может рассматриваться как случайная функция двух пространственных аргументов. Это случайное поле, заданное множеством своих реализаций на плоскости, описывается совокупностью функций распределения.

Дискретизация сигнала может осуществляться как во времени, так и в пространственных координатах.

Реальное изображение, подлежащее обработке на ЭВМ, имеет вполне ограниченные размеры, поэтому функция А (x,y) будет задана в области

[0, X _max] × [0, Y _max],

при этом дискретизация изображения позволяет выполнить преобразования:

А (x,y) ® A (m Dx, n Dy),

x Î [0, X _max], m = 0, 1, 2, ... , K-1; K =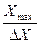

y Î [0, Y _max], n = 0, 1, 2, ... , L-1; L =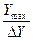

В результате двумерное изображение будет осуществлено с вещественной матрицей конечных размеров. Параметры дискретизации Dx и Dy определяют разрешающую способность дискретизации по пространственным аргументам.

Оптимальность дискретизации по теореме Котельникова определяется тем, что при выборе шага дискретизации равным

D l = ,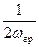

где w_гр - граничная частота в спектре сигнала А. Можно восстановить полный спектр дискретизируемого сигнала, причем это относится как ко времени, так и к пространственным координатам.

Реально выбор граничных частот для сигнала, изменяющего во времени (звука) и изображения несколько отличается. Пространственные частоты для большинства изображений имеют неограниченный спектр (много контрастных переходов). Однако реально выбор ограничений по спектру частот определяется с учетом особенностей классов изображений, подлежащих обработке - размеров минимальных деталей, наличия текстурных особенностей - например, неинформационных однородных зон и т.п. Поэтому выбирают пространственное разрешение системы и именно она связана с максимальной пространственной частотой.

В реальной ЭВМ ее характеристики и возможности по решению задач обработки больших массивов информации определяются многими причинами, и, в первую очередь, разрядностью ЭВМ, т.е. количеством двоичных разрядов, которые могут быть использованы для кодирования информации в одной точке. Именно с этого параметра ЭВМ можно говорить о количестве информации, принимаемой ЭВМ, точности решения задачи и т.д.

Контрольные вопросы

1. С какими видами информации Вам приходится сталкиваться? Чем они отличается друг от друга?

2. Как связано между собой структурно-аналитическое описание моделей и систем преобразования информации? Приведите примеры.

3. Приведите геометрическое толкование форм представления информации и ее дискретизации.

4. Какие этапы устранения избыточности необходимо пройти для формирования сигналов, обеспечивающих решение и воздействие на внешний объект?

5. Как информационно обеспечивается дискретизация и ввод изображений в ЭВМ? Приведите пример.

Глава 2