Лекция №3. Анализ и синтез последовательностных устройств

Содержание лекции:анализ работы типовых последовательностных схем, этапы синтеза последовательностного устройства.

Цели лекции:изучить работу триггеров, получить навыки анализа работы типовых последовательностных схем, освоить методику синтеза конечных автоматов.

Последовательностное устройство или конечный автомат – это устройство, выход которого определяется не только состоянием его входа, но и тем состоянием, в котором оно находилось в предшествующий момент времени. На рисунке 7 представлена одна из разновидностей конечного автомата, называемого автоматом Мура.

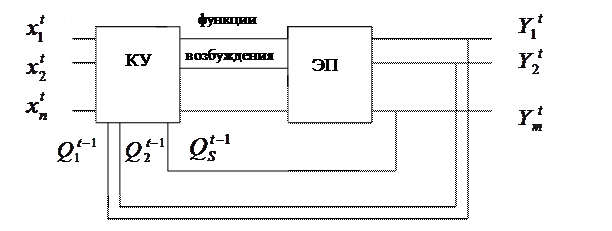
Рисунок 7 – Схема автомата Мура

Как видно из рисунка 7, конечный автомат состоит из комбинационного устройства и элементов памяти (ЭП), в качестве которых применяют триггеры. Аналитически работу автомата можно записать как

.

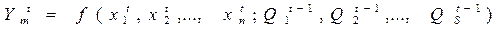Синтез конечного автомата сводится к определению типа и количества элементов памяти, а также схемы комбинационного устройства в выбранном базисе.

Триггер – это простейший автомат, который обладает двумя устойчивыми состояниями (1 и 0) и способен переходить из одного состояния в другое под воздействием входных сигналов. При определенной комбинации входных сигналов триггер не изменяет своего состояния, то есть он способен хранить один бит информации, поэтому он является элементарной ячейкой памяти и часто используется для организации триггерных структур памяти.

По способу управления триггеры подразделяют на асинхронные, переключение которых непосредственно зависит от входных сигналов, и синхронные, переключение которых возможно только с поступлением синхроимпульса на специальный вход С, который может иметь как статическое, так и динамическое управление. В первом случае триггеры реагируют на информационные сигналы при подаче на вход С уровня логической 1 (прямой вход) или логического 0 (инверсный вход). Во втором случае триггеры воспринимают информационные сигналы при изменении сигнала на вход С от 0 до 1 (прямой динамический вход) или от 1 до 0 (инверсный динамический вход). Синхронные триггеры со статическим управлением могут иметь двухступенчатую структуру, поэтому они всегда срабатывают по заднему фронту синхроимпульса.

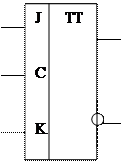
По функциональным возможностям триггеры подразделяют на асинхронные RS-триггеры с прямыми или инверсными входами, универсальный синхронный JK-триггер, Т-триггер (счетный триггер) и D-триггер (триггер задержки). На рисунке 8 соответственно представлены графические обозначения этих триггеров.

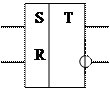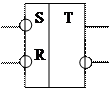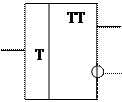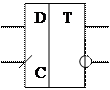Рисунок 8 – Графические обозначения разных типов триггеров

Как видно из рисунка 8, у всех триггеров для удобства использования предусмотрено два выхода: прямой и инверсный. Выходы триггеров принято обозначать: буквой 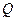- прямой выход и 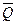- инверсный выход.

Переключение RS-триггера с прямыми входами в состояние логической 1 происходит при S=1,R=0, а в состояние логического 0 при S=0, R=1, при этом вход S называется входом установки, а вход R – сбросом. При S=R=0, триггер хранит 1 бит информации, а комбинация S=R=1 – запрещена в силу неопределенности состояния триггера. RS-триггер с инверсными входами делает все наоборот.

JK-триггер реагирует на входные информационные сигналы только при поступлении прямоугольного импульса на вход синхронизации С. Переключение JK-триггера происходит так же, как у RS-триггера с прямыми входами, принимая, что J=S а K=R, за исключением одной комбинации J=R=1, при которой триггер будет переключаться в противоположное состояние при поступлении очередного синхроимпульса, а так работает Т-триггер. Отсюда вытекает способ построения Т-тиггера из JK-триггера.

D-триггер способен задерживать прохождение информационного сигнала cо входа D на выход 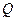до поступления очередного синхроимульса, подаваемого на вход синхронизации С.

Путем последовательного соединения триггеров можно построить такие типовые последовательностные устройства, как регистры и двоичные счетчики. В первом случае используют D-триггеры, во втором – T-триггеры.

Регистры предназначены для записи, хранения и выдачи информации в виде двоичного кода числа. Занесение новой информации в регистр называется записью, ее вывод – считыванием, а установка в нулевое состояние – сбросом. Если запись и считывание производятся параллельно, то есть всеми разрядами одновременно, то регистр называется параллельным. Достоинство таких регистров – высокое быстродействие. Регистр , в котором код записывается и считывается последовательно во времени, то есть разряд за разрядом, называется последовательным. Достоинство таких регистров – возможность сдвигать двоичную информацию вправо или влево.

Цифровой счетчик называется двоичным, если его коэффициент счета ( 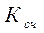) будет равен по модулю два, то есть 2,4,8 и т.д. Коэффициент счета – это то количество счетных импульсов, которые надо подать на вход счетчика, чтобы он вернулся в исходное состояние. Если 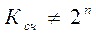, где n – целое положительное число, то счетчик называется недвоичным. У суммирующего счетчика исходное состояние равно нулю, а с приходом очередного счетного импульса его состояние будет увеличиваться на 1. У вычитающего счетчика исходное состояние равно 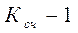, а с приходом очередного счетного импульса его состояние будет уменьшаться на 1. Реверсивные счетчики могут работать как в режиме сложения, так и вычитания.

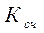Типовые разновидности регистров и счетчиков обычно выпускают в виде цифровых микросхем. Нетиповые регистры или счетчики можно синтезировать на базе логических элементов и триггеров. В качестве примера рассмотрим синтез синхронного счетчика на базе JK-триггеров с = 3.

1. Синхронный счетчик с 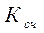= 3 строится на основе двоичного счетчика, состоящего из двух JK-триггеров, так как

n = ] log 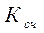[ = ] log 3 [ » 2 ,

где n – число триггеров в счетчике;

]log 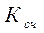[ - двоичный логарифм, округленный до большого целого числа.

2. Число избыточных состояний счетчика равно М =2² – 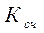= 4 – 3 = 1,

где: 2² – число устойчивых состояний двоичного счетчика.

3. Граф переходов счетчика и матрица переходов JK-триггера имеют вид, представленный на рисунке 9.

Вид перехода Входные сигналы

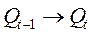
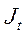
0 0 0 Ф

0 1 1 Ф

11 - избыточное состояние (*) 1 0 Ф 1

Ф – факультативное состояние 1 1 Ф 0

Рисунок 9 – Граф переходов счетчика и матрица переходов JK - триггера

4. На основании графа и матрицы строим таблицу 3.

Т а б л и ц а 3

Q2	Q1	J2	K2	J1	K1
K2 = K1 = 1 0			Ф		Ф
			Ф	Ф
		Ф			Ф

5. Полученные в таблице 3 функции возбуждения минимизируем с помощью двух карт Карно, представленных на рисунке 10.

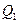0 1 0 1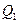

0 1

1 Ф

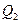
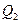
0 0 1 11

1 1

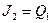
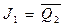
Рисунок 10 – Карты Карно на четыре клетки

6. На рисунке 11 представлена схема реализации синтезируемого счетчика, полученная на основе минимизированных логических функций.

1

& TT J C & K

& TT J C & K

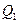
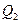
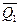Q₂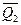

Рисунок 11 – Схема недвоичного счетчика