Алгоритм обратного распространения ошибки
Данный алгоритм используется для полно связной сети.
Wij –связь, соединяющая i-ый нейрон предыдущего слоя с j-ым нейроном последующего слоя.
Ошибка распространяется от выхода в сети к входам, т.е. направлении обратном функционированию сети в обычном режиме. Для минимизации ошибки используется функция отвеса
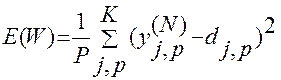
yj,p - реальное состояние нейрона выходного слоя N при подаче на входы сети примера P
P=1,p – множество примеров d – желаемый выход нейрона для данного входного примера p.
В процессе обучения выполняется минимизация ошибки E(W) методом градиентного спуска. Настройка весов осуществляется по правилу
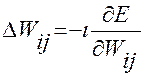(0<i<1) (1)
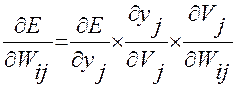
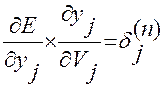
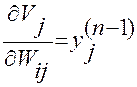
Для расчета величины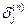 
вводится рекурсивная формула для расчета 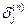через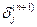 
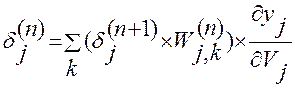
k – количество нейронов слоя (n+1) Для выходного слоя можно вычислить
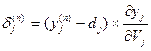Теперь перепишем формулу (1) в раскрытом виде
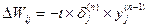
Алгоритм:
1) на входы подается один из возможных примеров из множества P
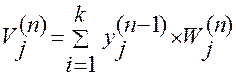
у каждого нейрона для получения выходного сигнала используется сигмоидная функция активации.
2) по формуле (4) вычисляется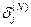 
для выходного слоя.
3) по формуле (3) вычисляется ошибка на предыдущем слое через последующий и по формуле (5) величина коррекции веса. Ошибки вычисляются для слов от N-1 до 1, т.е. n=N-1,…..,1
4) корректируются все веса связей в нейронной сети
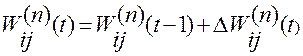
5) если общая ошибка E(W) больше заданной, то возвращаемся на шаг 1.
16 Способы обеспечения и ускорения сходимости
1. Начальное распределение весов. Инициализация весов связей. Весам связей присваиваются случайные малые значения, которые так же могу учитывать специфику задачи. Это необходимо для выведения системы из состояния равновесия.
Способы изменения весов:
1) Классический подход. Учитывая, что функция имеет максимальные значения от -3 до 3, то выбирают из интервала случайным образом [-3/корень(n); 3/корень(n)] где n – размерность сети во входном слое.
2) Инициализация весов по прототипам, полученным из кластеров обучающего множества
2. Обход локальных минимумов. Методы “удара”, “игра жизнь” и т.д. Для достижения глобального минимума на пов-ти ошибки используется ряд способов:
a.Расширение размерности пр-ва весов за счёт увеличения количества скрытых слоёв и увеличения количества нейронов в скрытых слоях.
b.Эвристический подход оптимизации (использование генетического алгоритма)
3. Упорядочивание данных, «взбалтывание». Множество примеров упорядочивают случайным образом, что позволяет избавиться от случайно образованной тенденции.
Если некоторые примеры представлены в недостаточном объёме , то их подают на сеть чаще остальных.
4. Пакетная обработка. Веса связей подстраиваются не после каждого примера, а путём усреднения по множеству примеров. Минимизация величины ошибки выполняется с помощью градиентных методов:
1) Используется градиент общей ошибки, вычисляемый после просчёта всего обучающегося множества (т.н. “эпоха”)τ - задаётся пользователем и называется величиной градиенты шага.
2) Стохастический градиентный метод. Пересчёт выполняется после всего множества примеров, но используется частная производная функции ошибки для K-го множества.
Если в начале обучения брать небольшие размеры пакетов, а затем их увеличить до общего количества, то скорость обучения уменьшается, а сходимость к глобальному решению остаётся. Такой подход используется при большом количестве примеров или при большой размерности.
5. Импульс. При определении направления поиска к текущему градиенту добавляется поправка (вектор смещения с предыдущего шага, взятый с некоторым коэффициентом)
Метод импульса чувствителен к способу упорядочивания примеров.
6. Управление величиной шага. При небольшом шаге процесс обучения будет медленным, а при большом шаге можно проскочить глобальный минимум. Величина шага обычно уменьшается в процессе обучения. Если при изменении связи ошибка уменьшилась, то шаг увеличивается – «поощрение», и наоборот – «наказание».