Двухточечный кроссинговер
Алгоритмы применяемые в глобальной поисковой оптимизации
Генетический
Генетические алгоритмы – это адаптивные методы поиска, которые в последнее время используются для решения задач оптимизации. В них используются как аналог механизма генетического наследования, так и аналог естественного отбора.
Эти алгоритмы успешно применяются в различных областях деятельности (экономика, физика, технические науки и т.п.). Созданы различные модификации ГА и разработан ряд тестовых функций.
Изначально новый алгоритм получил название «репродуктивный план Холланда» и в дальнейшем активно использовался в качестве базового алгоритма в эволюционных вычислениях. Идеи Холланда развили его ученики Кеннет Де Йонг (Kenneth De Jong) из университета Джорджа Мейсона (Вирджиния) и Дэвид Голдберг (David E. Goldberg) из лаборатории ГА Иллинойса. Благодаря им, был создан классический ГА, описаны все операторы и исследовано поведение группы тестовых функций (именно алгоритм Голдберга и получил название «генетический алгоритм»).
Генетический метод представляет собой скорее популяционно- генетический подход к решению задачи поиска, чем единый алгоритм решения дискретных оптимизационных задач. Таким образом, генетический метод образует класс алгоритмов поисковой оптимизации, основанных на математическом моделировании биологических механизмов и процессов в живой природе с помощью принципов популяционной генетики, которые позволяют находить оптимальные или близкие к ним (субоптимальные) решения. Информационная технология решения задач дискретной оптимизации с помощью алгоритмов поиска, реализующих генетический метод, основывается на использовании аналогов с эволюционными процессами скрещивания, кроссовера, мутации и естественного отбора. Основные формализованные элементы информационной технологии подробно рассматриваются в пособии: типы представлений дискретных решений; схемы скрещивания; генетические операторы кроссовера и мутации; процедуры селекции; выбор параметров генетического метода, для обеспечения сходимости к субоптимальным решениям. Особое внимание в пособии уделено представлению в виде перестановок и представлениям, эквивалентным перестановочному (порядковое, угловое и представление смежности). Для каждого представления рассмотрен ряд генетических операторов кроссовера, которые формируют новые решения в виде перестановок на основе уже имеющихся перестановок. Генетические методы не гарантируют обнаружения глобального оптимума за полиномиальное время, ибо только использование метода полного перебора позволяет найти решение глобальной оптимизации. Однако генетический алгоритм позволяет выбрать «достаточно хорошее» решение за меньшее время, чем другие известные детерминированные или эвристические алгоритмы поисковой оптимизации. Применение генетических методов для решения NP-трудных комбинаторных задач оптимизации полезно тогда, когда необходимый объем вычислительных затрат может оказаться большим, но скорость, с которой этот объем увеличивается при экспоненциальном росте «размерности» задачи дискретной оптимизации, часто может расти лишь линейно. Нереально ожидать, что можно найти один, общий генетический алгоритм, который бы хорошо решал любую задачу дискретной оптимизации. Однако можно попытаться подобрать представления, операторы и параметры генетического алгоритма, адаптированного для конкретной задачи таким образом, чтобы они выполнялись оптимально или лучше, чем выбранные случайным образом.
Классический (одноточечный) кроссинговер.
"Традиционный" генетический алгоритм использует одноточечный кроссинговер, в котором две скрещивающиеся хромосомы разрезаются один раз в соответствующей точке и производится обмен полученными частями. Однако было изобретено много других различных алгоритмов с иными видами кроссинговера, часто включающих больше чем одну точку разреза. DeJong исследовал эффективность многоточечного кроссинговера и пришел к выводу, что двухточечный кроссинговер дает улучшение, но что дальнейшее добавление точек кроссинговера редуцирует деятельность генетического алгоритма. Проблема с добавлением дополнительных точек кроссинговера состоит в том, что стандартные блоки, вероятно, будут прерваны. Однако преимущество большего количества точек кроссинговера состоит в том, что пространство состояний может быть исследовано более полно и подробно.
Двухточечный кроссинговер.
В двухточечном кроссинговере (и многоточечном кроссинговере вообще) хромосомы расцениваются как циклы, которые формируются соединением концов линейной хромосомы вместе. Для замены сегмента одного цикла сегментом другого цикла требуется выбор двух точек разреза. В этом представлении, одноточечный кроссинговер может быть рассмотрен как кроссинговер с двумя точками, но с одной точкой разреза, зафиксированной в начале строки. Следовательно, двухточечный кроссинговер решает ту же самую задачу, что и одноточечный кроссинговер , но более полно. Хромосома, рассматриваемая как цикл, может содержать большее количество стандартных блоков, так как они могут совершить "циклический возврат" в конце строки. В настоящий момент многие исследователи соглашаются, что двухточечный кроссинговер вообще лучше, чем одноточечный.
Преимущества генетических алгоритмов?
- Они не требуют никакой информации о поверхности ответа;
- Разрывы, существующие на поверхности ответа имеют незначительный эффект на полную эффективность оптимизации;
- Они стойки к попаданию в локальные оптимумы;
- Они хорошо работают при решении крупномасштабных проблем оптимизации;
- Могут быть использованы для широкого класса задач;
- Просты и прозрачны в реализации;
- Могут быть использованы в задачах с изменяющейся средой.
Недостатки генетических алгоритмов?
Не желательно и проблематично использовать ГА:
- В случае когда необходимо найти точный глобальный оптимум;
- Время исполнения функции оценки велико;
- Необходимо найти все решения задачи, а не одно из них;
- Конфигурация является не простой (кодирование решения).
Метод оптимизации с помощью роя частиц (Particle Swarm Optimization, далее PSO), базирующийся на моделировании поведения популяции частиц в пространстве параметров задачи оптимизации, был предложен в работе [1].
Предлагаемый метод привлекателен простотой реализации и тем, что в процессе вычисления не используется градиент. Метод может использоваться для решения многих задач, включая обучение нейросетей, задачи поиска минимума функции, а также задач, типичных для генетических алгоритмов.
PSO, как и все алгоритмы, принадлежащие к семейству эволюционных алгоритмов, является стохастическим, не требующим вычисления градиента, что позволяет использовать PSO в случаях, где вычисление градиента невозможно, либо имеет высокую вычислительную сложность.
Описание алгоритма PSO
Алгоритм PSO использует для решения рой частиц, где каждая частица представляет собой возможное решение задачи оптимизации. Пусть s - количество агентов в рое. Каждая i-ая частица может быть представлена как объект с рядом параметров.
· xi - положение частицы
· vi - скорость частицы
· yi - личное наилучшее положение частицы
Личное наилучшее положение частицы - положение частицы с наилучшим значением оценочной функции, которое когда-либо посещала частица. Пусть f - функция, которую необходимо минимизировать, тогда выражение для наилучшего личного положения в зависимости от времени:
yi  t+1
t+1  =
= 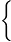 yi
yi  t
t  if f
if f  xi
xi  t+1
t+1 

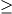 f
f  yi
yi  t
t 
 xi
xi  t+1
t+1  if f
if f  xi
xi  t+1
t+1 

 f
f  yi
yi  t
t 

Существует две версии базового алгоритма PSO, называемые gbest и lbest. Разница заключается в том, с какими набором частиц взаимодействует каждая частица. Обозначим символом y  это взаимодействие. Определение y
это взаимодействие. Определение y  в случае gbest представлено в следующем выражении:
в случае gbest представлено в следующем выражении:
y 

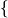 y0
y0  t
t 
 y1
y1  t
t 


 ys
ys  t
t 
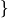
 f
f  y
y 
 t
t 
 =min
=min 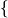 f
f  y0
y0  t
t 

 f
f  y1
y1  t
t 





 f
f  ys
ys  t
t 

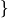
Данное выражение говорит о том, что y  - лучшая позиция когда-либо посещенная кем-либо из роя.
- лучшая позиция когда-либо посещенная кем-либо из роя.
Стохастическая составляющая алгоритма представлена двумя случайными параметрами r1  U
U  0
0  1
1  и r2
и r2  U
U  0
0  1
1  , которые масштабируются с помощью постоянных коэффициентов ускорения c1 и c2, отвечающих за величину шага, который может сделать частица за одну итерацию времени. Как правило c1
, которые масштабируются с помощью постоянных коэффициентов ускорения c1 и c2, отвечающих за величину шага, который может сделать частица за одну итерацию времени. Как правило c1  c2
c2 
 0
0  2] . Скорость частицы на i-м шаге расчитывается отдельно для каждого измерения j
2] . Скорость частицы на i-м шаге расчитывается отдельно для каждого измерения j  1
1 
 n , таким образом vi
n , таким образом vi  j обозначает j-е измерение вектора скорости i-й частицы. Расчет j-го компонента вектора скорости i-й частицы на t+1 шаге производится по формуле:
j обозначает j-е измерение вектора скорости i-й частицы. Расчет j-го компонента вектора скорости i-й частицы на t+1 шаге производится по формуле:
vi  j
j  t+1
t+1  =wcvi
=wcvi  j
j  t
t  +c1r1
+c1r1  t
t 
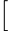 yi
yi  j
j  t
t  −xi
−xi  j
j  t
t 
 +c2r2
+c2r2  t
t 
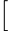 y
y 
 t
t  −xi
−xi  j
j  t
t 

Таким образом, c2 управляет воздействием глобального лучшего положения, а c1 управляет воздействием личного лучшего положения на скорость каждой частицы. Для улучшения сходимости алгоритма вводится коэффициент инерции wc [2]. Положение каждой частицы в i-м измерении вычисляется по формуле
xi  t+1
t+1  =xi
=xi  t
t  +vi
+vi  t+1
t+1 
Подготовительная часть алгоритма заключается в следующем :
1. Присвоить координатам xi  j случайные значения в пределах
j случайные значения в пределах 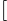 −xmax
−xmax  xmax
xmax  для всех i
для всех i  1
1 
 s и j
s и j  1
1 
 n,
n,
2. Инициализировать векторы скоростей нулями,
3. Присвоить yi значения xi.
